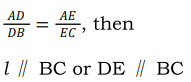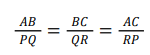Your cart is currently empty!
Level: Chapter
Chapter Level Content
POLYNOMIALS | Study
COORDINATE GEOMETRY | Study
LINEAR EQUATIONS IN TWO VARIABLES | Study
INTRODUCTION TO EUCLID’S GEOMETRY | Study
LINES AND ANGLES | Study
TRIANGLES | Study
QUADRILATERALS | Study
CIRCLES | Study
HERON’S FORMULA | Study
Integers | Assess
The Triangle and its Properties | Assess
Comparing Quantities | Assess
Rational Numbers | Assess
Simple Equations | Assess
Lines and Angles | Assess
Perimeter and Area | Assess
Algebraic Expressions | Assess
Exponents and Powers | Assess
Symmetry | Assess
Visualising Solid Shapes | Assess
Nutrition in Plants | Assess
Nutrition in Animals | Assess
Heat | Assess
Acids, Bases and Salts | Assess
POLYNOMIALS | Study
Mind Map Overal Idea Content Speed Notes Quick Coverage Polynomial A polynomial is an algebraic expression that includes constants, variables, and exponents. It is the expression in which the variables have only positive integral powers. Example 1. 4×3 + 3×2 + x +3 is a polynomial in variable x. 2. 4×2 + 3x-1 – 4… readmore
Mind Map
Overal Idea
Content
Speed Notes
Quick Coverage
Polynomial
A polynomial is an algebraic expression that includes constants, variables, and exponents. It is the expression in which the variables have only positive integral powers.
Example
1. 4x3 + 3x2 + x +3 is a polynomial in variable x.
2. 4x2 + 3x-1 – 4 is not a polynomial as it has negative power.
3. 3x3/2 + 2x – 3 is not a polynomial.
2 is the constant term, which has no variable.(Scroll down till end of the page)
Polynomials are denoted by p (x), q (x), etc.
In the above polynomials, 2x2, 3y, and 2 are the terms of the polynomial.
2 and 3 are the coefficients of x2 and y, respectively.
x and y are the variables.
Study Tools
Audio, Visual & Digital Content
Polynomial
A polynomial is an algebraic expression that includes constants, variables, and exponents. It is the expression in which the variables have only positive integral powers.
Example
1. 4x3 + 3x2 + x +3 is a polynomial in variable x.
2. 4x2 + 3x-1 – 4 is not a polynomial as it has negative power.
3. 3x3/2 + 2x – 3 is not a polynomial.
- Polynomials are denoted by p (x), q (x), etc.
- In the above polynomials, 2x2, 3y, and 2 are the terms of the polynomial.
- 2 and 3 are the coefficients of x2 and y, respectively.
- x and y are the variables.
- 2 is the constant term, which has no variable.
Polynomials in One Variable
If there is only one variable in the expression, then this is called the polynomial in one variable.
Example
- x3 + x – 4 is polynomial in variable x and is denoted by p(x).
- r2 + 2 is polynomial in variable r and is denoted by p(r).
Types of polynomials on the basis of the number of terms
Types of polynomials on the basis of the number of degrees
The highest value of the power of the variable in the polynomial is the degree of the polynomial.
Zeros of a Polynomial
If p(x) is a polynomial, then the number ‘a’ will be the zero of the polynomial with p(a) = 0. We can find the zero of the polynomial by equating it to zero.
Example: 1
The given polynomial is p(x) = x – 4
To find the zero of the polynomial, we will equate it to zero.
x – 4 = 0
x = 4
p(4) = x – 4 = 4 – 4 = 0
This shows that if we place 4 in place of x, we get the value of the polynomial as zero. So 4 is the zero of this polynomial. And also, we are getting the value 4 by equating the polynomial with 0.
So 4 is the zero of the polynomial or the root of the polynomial.
The root of the polynomial is basically the x-intercept of the polynomial.
If the polynomial has one root, it will intersect the x-axis at one point only, and if it has two roots, it will intersect at two points, and so on.
Example: 2
Find p (1) for the polynomial p (t) = t2 – t + 1
p (1) = (1)2 – 1 + 1
= 1 – 1 + 1
= 1
Remainder Theorem
We know the property of division which follows in the basic division, i.e.
Dividend = (Divisor × Quotient) + Remainder
This follows the division of polynomials.
If p(x) and g(x) are two polynomials in which the degrees of p(x) ≥ degree of g(x) and g(x) ≠ 0 are given, then we can get the q(x) and r(x) so that:
P(x) = g(x) q(x) + r(x),
where r(x) = 0 or degree of r(x) < degree of g(x).
It says that p(x) divided by g(x), gives q(x) as a quotient and r(x) as a remainder.
Let’s understand it with an example
Division of a Polynomial with a Monomial
We can see that ‘x’ is common in the above polynomial, so we can write it as
Hence, 3x2 + x + 1 and x the factors of 3x3 + x2 + x.
Steps of the Division of a Polynomial with a Non –Zero Polynomial
Divide x2 – 3x -10 by 2 + x
Step 1: Write the dividend and divisor in descending order, i.e., in the standard form. x2 – 3x -10 and x + 2
Divide the first term of the dividend with the first term of the divisor.
x2/x = x this will be the first term of the quotient.
Step 2: Now multiply the divisor by this term of the quotient and subtract it from the dividend.
Step 3: Now the remainder is our new dividend, so we will repeat the process again by dividing the dividend by the divisor.
Step 4: – (5x/x) = – 5
Step 5:
The remainder is zero.
Hence x2 – 3x – 10 = (x + 2)(x – 5) + 0
Dividend = (Divisor × Quotient) + Remainder
The Remainder Theorem says that if p(x) is any polynomial of degree greater than or equal to one and let ‘t’ be any real number and p (x) is divided by the linear polynomial x – t, then the remainder is p(t).
As we know,
P(x) = g(x) q(x) + r(x)
If p(x) is divided by (x-t) then
If x = t
P (t) = (t – t). q (t) + r = 0
To find the remainder or to check the multiple of the polynomial, we can use the remainder theorem.
Example:
What is the remainder if a4 + a3 – 2a2 + a + 1 is divided by a – 1.
Solution:
P(x) = a4 + a3 – 2a2 + a + 1
To find the zero of (a – 1), we need to equate it to zero.
a -1 = 0
a = 1
p (1) = (1)4 + (1)3 – 2(1)2 + (1) + 1
= 1 + 1 – 2 + 1 + 1
= 2
So by using the remainder theorem, we can easily find the remainder after the division of the polynomial.
Factor Theorem
The factor theorem says that if p(y) is a polynomial with degree n≥1 and t is a real number, then
- (y – t) is a factor of p(y), if p(t) = 0, and
- P (t) = 0 if (y – t) is a factor of p (y).
Example: 1
Check whether g(x) = x – 3 is the factor of p(x) = x3 – 4x2 + x + 6 using the factor theorem.
Solution:
According to the factor theorem, if x – 3 is the factor of p(x), then p(3) = 0, as the root of x – 3 is 3.
P (3) = (3)3 – 4(3)2 + (3) + 6
= 27 – 36 + 3 + 6 = 0
Hence, g (x) is the factor of p (x).
Example: 2
Find the value of k, if x – 1 is a factor of p(x) = kx2 – √2x + 1
Solution:
As x -1 is the factor, p(1) = 0
Factorization of Polynomials
Factorization can be done by three methods
1. By taking out the common factor
If we have to factorise x2 –x then we can do it by taking x common.
x(x – 1) so that x and x-1 are the factors of x2 – x.
2. By grouping
ab + bc + ax + cx = (ab + bc) + (ax + cx)
= b(a + c) + x(a + c)
= (a + c)(b + x)
3. By splitting the middle term
x2 + bx + c = x2 + (p + q) + pq
= (x + p)(x + q)
This shows that we have to split the middle term in such a way that the sum of the two terms is equal to ‘b’ and the product is equal to ‘c’.
Example: 1
Factorize 6x2 + 17x + 5 by splitting the middle term.
Solution:
If we can find two numbers p and q such that p + q = 17 and pq = 6 × 5 = 30, then we can get the factors.
Some of the factors of 30 are 1 and 30, 2 and 15, 3 and 10, 5 and 6, out of which 2 and 15 is the pair which gives p + q = 17.
6x2 + 17x + 5 =6 x2 + (2 + 15) x + 5
= 6 x2 + 2x + 15x + 5
= 2 x (3x + 1) + 5(3x + 1)
= (3x + 1) (2x + 5)
Algebraic Identities 1. (x + y)2 = x2 + 2xy + y2 2. (x – y)2 = x2 – 2xy + y2 3. (x + y) (x – y) = x2 – y2 4. (x + a) (x + b) = x2 + (a + b)x + ab 5. (x + y + z)2 = x2 + y2 + z2 + 2xy + 2yz + 2zx 6. (x + y)3 = x3 + y3 + 3xy(x + y) = x3+ y3 + 3x2y + 3xy2 7. (x – y)3 = x3– y3 – 3xy(x – y) = x3 – y3 – 3x2y + 3xy2 8. x3 + y3 = (x + y)(x2 – xy + y2) 9. x3 – y3 = (x – y)(x2 + xy + y2) 10. x3 + y3 + z3 – 3xyz = (x + y + z)(x2 + y2 + z2 – xy – yz – zx) x3 + y3 + z3 = 3xyz if x + y + z = 0 Example: 2
Factorize 8x3 + 27y3 + 36x2y + 54xy2
Solution:
The given expression can be written as
= (2x)3 + (3y)3 + 3(4x2) (3y) + 3(2x) (9y2)
= (2x)3 + (3y)3 + 3(2x)2(3y) + 3(2x)(3y)2
= (2x + 3y)3 (Using Identity VI)
= (2x + 3y) (2x + 3y) (2x + 3y) are the factors.
Example: 3
Factorize 4x2 + y2 + z2 – 4xy – 2yz + 4xz.
Solution:
4x2 + y2 + z2 – 4xy – 2yz + 4xz = (2x)2 + (–y)2 + (z)2 + 2(2x) (-y)+ 2(–y)(z) + 2(2x)(z)
= [2x + (- y) + z]2 (Using Identity V)
= (2x – y + z)2 = (2x – y + z) (2x – y + z)
Hindi Version Key Terms
Topic Terminology
Term
Important Tables
Table:
.
COORDINATE GEOMETRY | Study
Mind Map Overal Idea Content Speed Notes Quick Coverage Cartesian System A plane formed by two number lines, one horizontal and the other vertical, such that they intersect each other at their zeroes, and then they form a Cartesian Plane. (Scroll down till end of the page) Study Tools Audio, Visual & Digital Content ●… readmore
Mind Map
Overal Idea
Content
Speed Notes
Quick Coverage
Cartesian System

A plane formed by two number lines, one horizontal
and the other vertical, such that they intersect each
other at their zeroes, and then they form a Cartesian
Plane.
(Scroll down till end of the page)
Study Tools
Audio, Visual & Digital Content
● The horizontal line is known as the x-axis and the vertical line is known
as the y-axis.
● The point where these two lines intersect each other is called the origin.
It is represented as ‘O’.
● OX and OY are the positive directions as the positive numbers lie in the
right and upward direction.
● Similarly, the left and the downward directions are the negative directions
as all the negative numbers lie there.

Quadrants of the Cartesian Plane The Cartesian plane is divided into four quadrants namely Quadrant I, Quadrant II, Quadrant III, and Quadrant IV anticlockwise from OX.

Coordinates of a Point To write the coordinates of a point we need to follow the following rules. ● Thex – coordinate of a point is marked by drawing perpendicular from the y-axis measured a length of the x-axis .It is also called the Abscissa.

They – coordinate of a point is marked by drawing a perpendicular from the x-axis measured a length of the y-axis .It is also called the Ordinate. ● While writing the coordinates of a point in the coordinate plane, the x – coordinate comes first, and then the y – coordinate. We write the coordinates in brackets. In figure, OB = CA = x coordinate (Abscissa), and CO = AB = y coordinate (Ordinate). We write the coordinate as (x, y).
Remarks:

As the origin, O has zero distance from the x-axis and the y-axis so its abscissa and ordinate are zero. Hence the coordinate of the origin is (0, 0). The relationship between the signs of the coordinates of a point and the quadrant of a point in which it lies.

Plotting a Point in the Plane if its Coordinates are Given

Steps to plot the point (2, 3) on the Cartesian plane:
● First of all, we need to draw the Cartesian plane by drawing the coordinate axes with 1 unit = 1 cm.
● To mark the x coordinates, starting from 0 moves towards the positive x-axis and counts to 2.
● To mark the y coordinate, starting from 2 moves upwards in the positive direction and counts to 3.
● Now this point is the coordinate (2, 3). Likewise, we can plot all the other points, like (-3, 1) and (-1.5,-2.5) in the figure.
Question: Are the coordinates (x, y) = (y, x)? Let x = (-4) and y = (-2) So (x, y) = (- 4, – 2) (y, x) = (- 2, – 4)

Let’s mark these coordinates on the Cartesian plane. You can see that the positions of both the points are different in the Cartesian plane. So, If x ≠ y, then (x, y) ≠ (y, x), and (x, y) = (y, x), if x = y.
Example: Plot the points (6, 4), (- 6,- 4), (- 6, 4) and (6,- 4) on the Cartesian plane.

Solution: Since both numbers 6, 4 are positive the point (6, 4) lies in the first quadrant. For x coordinate, we will move towards the right and count to 6. Then from that point go upward and count to 4. Mark that point as the coordinate (6, 4). Similarly, we can plot all the other three points.
Hindi Version Key Terms
Topic Terminology
Term
Important Tables
Table:
.
LINEAR EQUATIONS IN TWO VARIABLES | Study
Mind Map Overal Idea Content Speed Notes Quick Coverage Linear Equations The equation of a straight line is the linear equation. It could be in one variable or two variables. Linear Equation in One Variable The equation with one variable in it is known as a Linear Equation in One Variable. (Scroll down to continue… readmore
Mind Map
Overal Idea
Content
Speed Notes
Quick Coverage
Linear Equations
The equation of a straight line is the linear equation. It could be in one variable or two variables.
Linear Equation in One Variable
The equation with one variable in it is known as a Linear Equation in One Variable. (Scroll down to continue …)
(Scroll down till end of the page)
Study Tools
Audio, Visual & Digital Content
The general form for Linear Equation in One Variable is px + q = s, where p, q and s are real numbers and p ≠ 0.
Example:
x + 5 = 10
y – 3 = 19
These are called Linear Equations in One Variable because the highest degree of the variable is one.
Graph of the Linear Equation in One Variable
We can mark the point of the linear equation in one variable on the number line.
x = 2 can be marked on the number line as follows –
Graph of the Linear Equation in One Variable
Linear Equation in Two Variables
An equation with two variables is known as a Linear Equation in Two Variables. The general form of the linear equation in two variables is
ax + by + c = 0
where a and b are coefficients and c is the constant. a ≠ 0 and b ≠ 0.
Example
6x + 2y + 5 = 0, etc.
Slope Intercept form
Generally, the linear equation in two variables is written in the slope-intercept form as this is the easiest way to find the slope of the straight line while drawing the graph of it.
The slope-intercept form is y = mx+c
Where m represents the slope of the line.
and c tells the point of intersection of the line with the y-axis.
Remark: If b = 0 i.e. if the equation is y = mx then the line will pass through the origin as the y-intercept is zero.
Solution of a Linear Equation
There is only one solution in the linear equation in one variable but there are infinitely many solutions in the linear equation in two variables.
As there are two variables, the solution will be in the form of an ordered pair, i.e. (x, y).
The pair which satisfies the equation is the solution to that particular equation.
Example:
Find the solution for the equation 2x + y = 7.
Solution:
To calculate the solution of the given equation we will take x = 0
2(0) + y = 7
y = 7
Hence, one solution is (0, 7).
To find another solution we will take y = 0
2x + 0 = 7
x = 3.5
So another solution is (3.5, 0).
Graph of a Linear Equation in Two Variables
To draw the graph of a linear equation in two variables, we need to draw a table to write the solutions of the given equation, and then plot them on the Cartesian plane.
By joining these coordinates, we get the line of that equation.
The coordinates which satisfy the given Equation lie on the line of the equation.
Every point (x, y) on the line is the solution x = a, y = b of the given Equation.
Any point, which does not lie on the line AB, is not a solution of Equation.
Example:
Draw the graph of the equation 3x + 4y = 12.
Solution:
To draw the graph of the equation 3x + 4y = 12, we need to find the solutions of the equation.
Let x = 0
3(0) + 4y = 12
y = 3
Let y = 0
3x + 4(0) = 12
x = 4
Now draw a table to write the solutions.
x 0 4
y 3 0
Now we can draw the graph easily by plotting these points on the Cartesian plane.
Linear Equation in Two Variables
Equations of Lines Parallel to the x-axis and y-axis
When we draw the graph of the linear equation in one variable then it will be a point on the number line.
x – 5 = 0
x = 5
This shows that it has only one solution i.e. x = 5, so it can be plotted on the number line.
But if we treat this equation as the linear equation in two variables then it will have infinitely many solutions and the graph will be a straight line.
x – 5 = 0 or x + (0) y – 5 = 0
This shows that this is the linear equation in two variables where the value of y is always zero. So the line will not touch the y-axis at any point.
x = 5, x = number, then the graph will be the vertical line parallel to the y-axis.
All the points on the line will be the solution of the given equation.
Equations of Lines Parallel to the x-axis and y-axis
Similarly if y = – 3, y = number then the graph will be the horizontal line parallel to the x-axis.
Hindi Version Key Terms
Topic Terminology
Term
Important Tables
Table:
.
INTRODUCTION TO EUCLID’S GEOMETRY | Study
Mind Map Overal Idea Content Speed Notes Quick Coverage Introduction to Euclid Geometry The necessity of geometry had been felt from ancient times in different parts of the world. The practical problems faced by people of ancient civilization had developed this branch of mathematics. Let us cite few examples. With floods in the river, the… readmore
Mind Map
Overal Idea
Content
Speed Notes
Quick Coverage
Introduction to Euclid Geometry The necessity of geometry had been felt from ancient times in different parts of the world. The practical problems faced by people of ancient civilization had developed this branch of mathematics.
Let us cite few examples.
With floods in the river, the demarcations of land owners on the river-side land were used to wipe out (Scroll down till end of the page)
Study Tools
Audio, Visual & Digital Content
In order to redraw the boundaries, the idea of area was introduced, the idea of area was introduced.
The volumes of granaries could be measured by using geometry.
The existence of Egyptian pyramids indicates the use of geometry from olden times.
In Vedic period, there was a manual of geometrical construction, known as Sulbasutra’s.
Different geometrical shapes were constructed as altars to perform various Vedic rites.
The word Geometry originates from the green word ‘Geo’ (earth) and metrein (to measure) Through Geometry was developed and applied from ancient time in various part the world, it was not presented in a systematic manner.
Later in 300 BC, the Egyptian mathematician Euclid, collected all the known work and arranged it in a systematic manner.
‘Elements’ is a classic treatise in geometry which was written by Euclid.
This was the most influential book. The ‘element’ was used as a text book for several years in western Europe.
The ‘elements’ started with 28 definitions, five postulates and five common notions and systematically built the rest of plane and solid geometry.
The geometrical approach given by Euclid is known as Euclid method.
The Euclid method consists of making a small set of assumptions and then proving many other proposition from these assumptions.
The assumptions, made were obvious universal truth. The two types of assumption, made were ‘axioms’ and ‘postulates’.
Euclid’s Definitions Euclid listed 23 definitions in book 1 of the ‘elements’.
We list a few of them: 1) 2) 3) 4) 5) 6) 7) A point is that which has no part A line is a breadth less length The ends of a line are points A straight line is a line which lies evenly with the points on itself. A surface is that which has length and breadth only.
The edges of a surface are lines A plane surface is surface which lies evenly with straight lines on its self. Starting with these definitions, Euclid assumed certain assumptions, known as axioms and postulates.
Euclid’s Axioms Axioms were assumptions which were used throughout mathematics and are not specifically linked to geometry.
Few of Euclid’s axioms are:
1) Things which are equal to the same thing are equal to one another.
2) It equals are added to equals; the wholes are equal.
3) 4) 5) 6) 7) If equals are subtracted from equals, the remainders are equal.
Things which coincide one another are equal to one another.
The whole is greater than the part Things which are double of the same thing are equal to one another.
Things which are half of the same things are equal to one another.
All these axioms refer to magnitude of same kind.
Axiom – 1 can be written as follows: If x = Z and y = Z, then x = y
Axiom – 2 explains the following: If x = y, then x + Z = y + Z According to axiom – 3, If x = y, then x – Z = y – Z Axiom – 4 justifies the principle of superposition that every thing equals itself.
Axiom – 5, gives us the concept of comparison. If x is a part of y, then there is a quantity Z such that x = y + Z or x > y Note that magnitudes of the same kind can be added, subtracted or compared.
Euclid’s Postulates Euclid used the term postulate for the assumptions that were specific to geometry. Euclid’s five postulates are as follows: Postulate 1: A straight line may be drawn from any one point to any other point. Same may be stated as axiom 5.1 Given two distinct points, there is a unique line that passes through them.
Postulate 2: A terminated line can be produced indefinitely. Postulate 3: A circle can be drawn with any centre and any radius. Postulate 4: All right angles are equal to one another. Postulate 5: If a straight line falling on two straight lines makes the interior angle on the same side of it taken together less than two right angles, then two straight lines, if produced indefinitely, meet on that side on which the sum of the angles is less than two right angles. Postulates 1 to Postulates 4 are very simple and obvious and therefore they are taken a ‘self evident truths’. Postulates 5 is complex and it needs to be discussed. Suppose the line XY falls on two lines AB and CD such that ∠1 + ∠2 < 180°, then the lines AB and CD will intersect at a point. In the given figure, they intersect on left side of PQ, if both are produced. Note: In mathematics the words axiom and postulate may be used interchangeably, though they have distinct meaning according to Euclid. System of Consistent Axioms A system of axioms is said to be consistent, if it is impossible to deduce a statement from these axioms, which contradicts any of the given axioms or proposition. Proposition or Theorem The statement or results which were proved by using Euclid’s axioms and postulates are called propositions or Theorems. Theorem: Two distinct lines cannot have more than one point in common. Proof: Given: AB and CD are two lines. To prove: They intersect at one point or they do not intersect. Proof: Suppose the lines AB and CD intersect at two points P and Q. This implies the line AB passes through the points P and Q. Also the line CD passes through the points P and Q. This implies there are two lines which pass through two distinct point P and Q. But we know that one and only one line can pass through two distinct points. This axiom contradicts out assumption that two distinct lines can have more than one point in common. The lines AB and CD cannot pass through two distinct point P and Q. Equivalent Versions of Euclid’s Fifth Postulate The two different version of fifth postulate a) For every line l and for every point P not lying on l, there exist a unique line m passing through P and parallel to l. b) Two distinct intersecting lines cannot be parallel to the same line.
Key Terms
Topic Terminology
Term
Important Tables
Table:
.
LINES AND ANGLES | Study
Mind Map Overal Idea Content Speed Notes Quick Coverage Basic terms and Definitions 1. Point – A Point is that which has no component. It is represented by a dot. 2. Line – When we join two distinct points then we get a line. A line has no endpoints; it can be extended on both… readmore
Mind Map
Overal Idea
Content
Speed Notes
Quick Coverage
Basic terms and Definitions

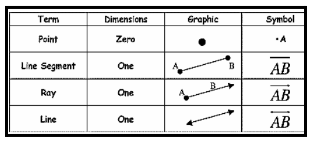
1. Point – A Point is that which has no component. It is represented by a dot.
2. Line – When we join two distinct points then we get a line. A line has no endpoints; it can be extended on both sides infinitely.
3. Line Segment Line – Segment is the part of the line which has two endpoints.
4. Ray – Ray is also a part of the line that has only one endpoint and has no end on the other side.
5. Collinear points: Points lying on the same line are called Collinear Points.
6. Non-collinear points: Points which do not lie on the same line are called Non-Collinear Points. (Scroll to continue …)
(Scroll down till end of the page)
Study Tools
Audio, Visual & Digital Content
Angles
When two rays begin from the same endpoint then they form an Angle. The two rays are the arms of the angle and the endpoint is the vertex of the angle.
Types of Angles
Angle Notation Image Acute An angle which is between 0° and 90°. Right An angle which is exactly equal to 90°. Obtuse An angle which is between 90° and 180°. Reflex An angle which is between 180° and 360° Straight An angle which is exactly equal to 180°. Complete An angle which is exactly equal to 360°. Types of Angles Complementary and Supplementary Angles
Complementary Angles are the different angles whose sum is 90°.
Complementary Angles are the different angles whose sum is 180°.

Intersecting Lines and Non-intersecting Lines
There are two ways to draw two lines-
1. The lines which cross each other from a particular point are called Intersecting Lines.
2. The lines which never cross each other at any point are called Non-intersecting Lines. These lines are called Parallel Lines and the common length between two lines is the distance between parallel lines.
Pairs of Angles Axioms
1. If a ray stands on a line, then the sum of two adjacent angles formed by that ray is 180°.
This shows that the common arm of the two angles is the ray which is standing on a line and the two adjacent angles are the linear pair of the angles. As the sum of two angles is 180° so these are supplementary angles too.
2. If the sum of two adjacent angles is 180°, then the arms which are not common of the angles form a line.
This is the reverse of the first axiom which says that the opposite is also true.
Vertically opposite Angles Theorem
When two lines intersect each other, then the vertically opposite angles so formed will be equal.
AC and BD are intersecting each other so ∠AOD = ∠BOC and ∠AOB = DOC.
Parallel Lines and a Transversal
If a line passes through two distinct lines and intersects them at distant points then this line is called Transversal Line.
Here line “l” is transversal of line m and n.
Exterior Angles – ∠1, ∠2, ∠7 and ∠8
Interior Angles – ∠3, ∠4, ∠5 and ∠6
Pairs of angles formed when a transversal intersects two lines-
1. Corresponding Angles:
- ∠ 1 and ∠ 5
- ∠ 2 and ∠ 6
- ∠ 4 and ∠ 8
- ∠ 3 and ∠ 7
2. Alternate Interior Angles:
- ∠ 4 and ∠ 6
- ∠ 3 and ∠ 5
3. Alternate Exterior Angles:
- ∠ 1 and ∠ 7
- ∠ 2 and ∠ 8
4. Interior Angles on the same side of the transversal:
- ∠ 4 and ∠ 5
- ∠ 3 and ∠ 6
Transversal Axioms
1. If a transversal intersects two parallel lines, then
- Each pair of corresponding angles will be equal.
- Each pair of alternate interior angles will be equal.
- Each pair of interior angles on the same side of the transversal will be supplementary.
2. If a transversal intersects two lines in such a way that
- Corresponding angles are equal then these two lines will be parallel to each other.
- Alternate interior angles are equal then the two lines will be parallel.
- Interior angles on the same side of the transversal are supplementary then the two lines will be parallel.
Lines Parallel to the Same Line
If two lines are parallel with a common line then these two lines will also be parallel to each other.
As in the above figure if AB ∥ CD and EF ∥ CD then AB ∥ EF.
Angle Sum Property of a Triangle
1. The sum of the angles of a triangle is 180º.
∠A + ∠B + ∠C = 180°
2. If we produce any side of a triangle, then the exterior angle formed is equal to the sum of the two interior opposite angles.
∠BCD = ∠BAC + ∠ABC.
Hindi Version Key Terms
Topic Terminology
Term
Important Tables
Table:
.
TRIANGLES | Study
Mind Map Overal Idea Content Speed Notes Quick Coverage Similar Geometric Figures: Two geometric figures which are the same in shape, such that one is simply a copy of the other on a smaller scale or a larger scale, are called similar geometric figures. Two geometric figures are said to be similar if and only… readmore
Mind Map
Overal Idea
Content
Speed Notes
Quick Coverage
Similar Geometric Figures:
Two geometric figures which are the same in shape, such that one is simply a copy of the other on a smaller scale or a larger scale, are called similar geometric figures.
Two geometric figures are said to be similar if and only if they have the same shape but not necessarily the same size. Two congruent geometric figures are always similar but converse may or may not be true. (Scroll down till end of the page)
Study Tools
Audio, Visual & Digital Content
Similar Polygons: Two polygons of the same number of sides are similar, if
(i) their corresponding angles are equal and
(ii) their corresponding sides are in proportion or their corresponding sides are in the same ratio.
The same ratio of the corresponding sides is referred to as the representative fraction or the scale factor for the polygons.
Similar Triangles :
Two triangles are said to be similar,
if (i) their corresponding angles are equal and
ii) their corresponding sides are in proportion (are in the same ratio).
Basic Proportionality Theorem (or Thales Theorem) : 1
If a line is drawn parallel to one side of a triangle intersecting the other two sides, then it divides the two sides in the same ratio. Or If a line is drawn parallel to one side of a triangle, intersecting the other two sides in distinct points, the other two sides are divided in the same ratio i .e.. If in ∆ABC, l∥ BC, intersecting in D and E. then

Converse of Basic Proportionality Theorem :

If a line divides any two sides of a triangle in the sameratio, the line is parallel to the third side i.e.
In ∆ABC, if l intersects AB in D and AC in E, such that:

Criteria for Similarity of Triangles:
Two triangles are said to be similar, if
(i) their corresponding angles are equal and (ii) their corresponding sides are in proportion (or are in the same ratio).
2 (i) AA or AAA Similarity Criterion : If two angles of one triangle are equal to two corresponding angles of another triangle, then the triangles are similar. If two angles of one triangle are respectively equal to the two angles of another triangle, then the third angles of the two triangles are necessarily equal, because the sum of three angles of a triangle is always 180 0 .
(ii) SAS Similarity Criterion : If one angle of a triangle is equal to one angle of another triangle and the sides including these angles are in the same ratio, then the two triangles are similar. Or If two sides of a triangle are proportional to two corresponding sides of another triangle and the angles included between them are equal, then the triangles are similar.
iii) SSS Similarity Criterion : If in two triangles, sides of one triangle are proportional (or are in the same ratio) to the sides of the other triangle, then the triangles are similar. If ∆ABC~ ∆PQR by any one similarity criterion, then ∠A=∠P, ∠B=∠Q, ∠C=∠R and

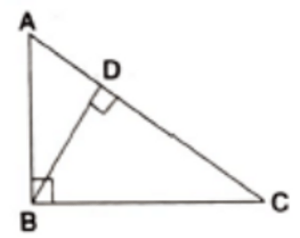
i.e., A and P, B and Q, C and R are the corresponding vertices, also AB and PQ. BC and QR. CA and RP are the corresponding sides. 3 Areas of Similar Triangles: The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides. – The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding medians. – The ratio of the areas of two similar triangles is equal to the ratio of the squares of their corresponding altitudes. – The ratio of the areas of two similar triangles is equal to the ratio of the squares of their corresponding angle bisectors. Pythagoras Theorem : In a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides. Converse of Pythagoras Theorem : In a triangle, if the square of one side is equal to the sum of the squares of the other two sides, then the angle opposite the first side is a right angle. If a perpendicular is drawn from the vertex of the right angle of a right triangle to the hypotenuse, the triangles on each side of the perpendicular are similar to the whole triangle and similar to each other i .e ..

If in ∆ABC, ∠B=90^0 and BD ⊥ AC, then (i) ∆ADB ~ ∆ABC (ii) ∆BDC ~ ∆ABC (iii) ∆ADB ~ ∆BDC
Hindi Version Key Terms
Topic Terminology
Term
Important Tables
Table:
.
QUADRILATERALS | Study
Mind Map Overal Idea Content Speed Notes Quick Coverage Quadrilateral Any closed polygon with four sides, four angles and four vertices are called Quadrilateral. It could be regular or irregular. (Sroll down to continute till the end …) Study Tools Audio, Visual & Digital Content Quadrilateral Quadrilateral is a closed figure with four sides. Characteristics… readmore
Mind Map
Overal Idea
Content
Speed Notes
Quick Coverage
Quadrilateral
Any closed polygon with four sides, four angles and four vertices are called Quadrilateral. It could be regular or irregular. (Sroll down to continute till the end …)
Study Tools
Audio, Visual & Digital Content
Quadrilateral
Quadrilateral is a closed figure with four sides.
Characteristics of a quadrilateral
Angle Sum Property of a Quadrilateral:
Qudrilateral is a four sided closed figure.
Sum of all angles of a quadrilateral is 360°.
Types Of Quadrilaterals

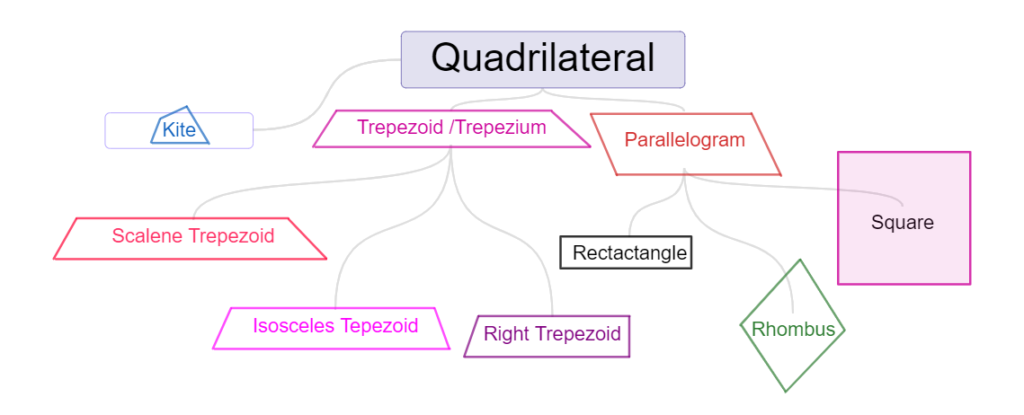
Classification of quadrilaterals Quadrilaterals are broadly classified into three categories as:
(i) Kite
(ii) Trapezium
(ii) Parallelogram
Kite:
(i) Kite has no parallel sides
(ii) Kite has a pair of equal adjacent sides.
(ii) It is not a parallelogram
Characteristics Of Kite:
Perimeter Of Square
Area Of Kite
Trapezium:
Trapezium is a quadrilateral with the following characteristics:
(i) One pair of opposite sides is parallel to each other.
(ii) The other pair of opposite sides may not be parallel to each other.
Characteristics Of Trapezium
(i) Sum of all angles of a quadrilateral is 360°.
(ii) One pair of opposite sides is parallel to each other.
(iii) The other pair of opposite sides need not be parallel to each other.
Types Of Trapezium:
Quadrilaterals are broadly classified into two categories as:
(i) Isosceles Trapezium.
(ii) Scalene Trapezium.
(i) Right Trapezium.
Isosceles Trapezium:
Isosceles Trapezium is a quadrilateral with the following characteristics:
(i) One pair of opposite sides is parallel to each other.
(ii) The other pair of opposite sides are equal.
(iii) The other pair of opposite sides need not be parallel to each other.
Isosceles Trapezium is a trapezium with the following characteristics:
(i) One pair of opposite sides is parallel to each other.
(ii) The other pair of opposite sides are equal.
(iii) The other pair of opposite sides need not be parallel to each other.
Characteristics Of Isosceles Trapezium
(i) Sum of all angles of a quadrilateral is 360°.
(ii) One pair of opposite sides is parallel to each other.
(iii) The other pair of opposite sides are equal.
(iv) The other pair of opposite sides need not be parallel to each other.
Scalene Trapezium:
- Scalene trapezium: Classified by the length of the legs or the measurement of their angles.
Characteristics Of Scalene Trapezium
Right Trapezium:
- Right trapezium: Has one pair of parallel sides and one pair of right angles.
Characteristics Of Right Trapezium
Perimeter Of Trapezium
Area Of Trapezium
Parallelogram:
Parallelogram is a quadrilateral with the following characteristics:
(i) Two pairs of opposite sides are parallel to each other.
(ii) Two pairs of opposite sides are equal in length.
Characteristics of a parallelogram
(i) Sum of all angles of a Parallelogram is 360°.
(ii) Two pairs of opposite sides are parallel to each other.
(ii) Two pairs of opposite sides are equal in length.
(ii) Two pairs of opposite angles are equal.
(iii) Diagonals bisect each other.
(iv) Diagonals need not be equal to each other.
(v) Diagonals divide it into two congruent triangles.
Types Of Parallelogram
Parallelograms are broadly classified into three categories as:
(i) Rectangle
(ii) Rhombus
(iii) Square
Perimeter Of Parallelogram
Area Of Parallelogram
Rectangle:
Rectangle is a quadrilateral with the following characteristics:
(i) Two pairs of opposite sides are parallel to each other.
(ii) Two pairs of opposite sides are equal in length.
(iii) All four angles are right angles. (each angle is 90 o).
Characteristics Of Rectangle
(i) Sum of all angles of a quadrilateral is 360°.
(ii) Two pairs of opposite sides are parallel to each other.
(ii) Two pairs of opposite sides are equal in length.
(iii) All four angles are right angles. (each angle is 90 o).
(iii) Diagonals bisect each other.
(iv) Diagonals are equal to each other.
(v) Diagonals of a rectangle divide it into two congruent triangles.
Conclusions:
- Every Rectangle is a Parallelogram. But Every Parallelogram need not to be a Rectangle.
Condition for a rhombus to be a square:
If all four angles of a parallelogram are right angles. (each angle is 90 o), the parallelogram becomes a Rectangle.
Perimeter Of Rectangle
Area Of Recatangle
Rhombus:
Rhombus is a quadrilateral with the following characteristics:
(i) Two pairs of opposite sides are parallel to each other.
(ii) All four sides are equal in length.
Characteristics Of Rhombus
(i) Sum of all angles of a quadrilateral is 360°.
(ii) Two pairs of opposite sides are parallel to each other.
(ii) All four sides are equal in length.
(ii) Two pairs of opposite angles are equal.
(iii) Diagonals bisect each other.
(iv) Diagonals need not be equal to each other.
(v) Diagonals divide a Rhombus into two congruent triangles.
Conclusions:
- Every Rhombus is a Parallelogram. But Every Parallelogram need not to be a Rhombus.
Condition for a rhombus to be a square:
If all the sides of a parallelogram are equal, the parallelogram becomes a Rhombus.
Perimeter Of Rhombus
Area Of Rhombus
Square:
Square is a quadrilateral with the following characteristics:
(i) Two pairs of opposite sides are parallel to each other.
(ii) All four sides are equal in length.
(iii) All four angles are right angles. (each angle is 90 o).
Characteristics Of Square
(i) Sum of all angles of a quadrilateral is 360°.
(ii) Two pairs of opposite sides are parallel to each other.
(iii) All four sides are equal in length.
(iv) All four angles are right angles. (each angle is 90 o).
(v) Diagonals bisect each other.
(vi) Diagonals need not be equal to each other.
(vii) Diagonals divide a Rhombus into two congruent triangles.
Conclusions:
- Every square is a Rhombus. But Every Rhombus need not to be a square.
Condition for a rhombus to be a square:
If all the angles of a rhombus are right angles (euqal to 90o), the rhombus becomes a square.
2. Every Square is a prallelogram. But Every prallelogram need not to be a square.
Condition for a prallelogram to be a square:
(i) If all the angles of a parallelogram are right angles (euqal to 90o), and all the sides of a parallelogram are equal in length, the parallelogram becomes a square.
3. Every Square is a rectangle. But Every Rectangle need not to be a square.
Condition for a Rectangle to be a square:
If all the sides of a Rectangle are equal in length, the Rectangle becomes a square.
If all the sides of a parallelogram are equal, the parallelogram becomes a Rhombus.
Perimeter Of Square
Area Of Square
Important Points To Remember
- The diagonals of a parallelogram are equal if and only if it is a rectangle.
- If a diagonal of a parallelogram bisects one of the angles of the parallelogram then it also bisects the opposite angle.
- In a parallelogram, the bisectors of any two consecutive angles intersect at a right angle.
- The angle bisectors of a parallelogram form a rectangle.
Mid Point Theorem
A line segment joining the mid points of any two sides of a triangle is parallel to the third side and length of the line segment is half of the parallel side.
Converse Of Mid Point Theorem
A line through the midpoint of a side of a triangle parallel to another side bisects the third side.
Intercept Theorem
If there are three parallel lines and the intercepts made by them on one transversal are equal then the intercepts on any other transversal are also equal.
Angle Sum Property of a Quadrilateral
The sum of the four angles of a quadrilateral is 360°
If we draw a diagonal in the quadrilateral, it divides it into two triangles.
And we know the angle sum property of a triangle i.e. the sum of all the three angles of a triangle is 180°.
The sum of angles of ∆ADC = 180°.
The sum of angles of ∆ABC = 180°.
By adding both we get ∠A + ∠B + ∠C + ∠D = 360°
Hence, the sum of the four angles of a quadrilateral is 360°.
Example
Find ∠A and ∠D, if BC∥ AD and ∠B = 52° and ∠C = 60° in the quadrilateral ABCD.
Solution:
Given BC ∥ AD, so ∠A and ∠B are consecutive interior angles.
So ∠A + ∠B = 180° (Sum of consecutive interior angles is 180°).
∠B = 52°
∠A = 180°- 52° = 128°
∠A + ∠B + ∠C + ∠D = 360° (Sum of the four angles of a quadrilateral is 360°).
∠C = 60°
128° + 52° + 60° + ∠D = 360°
∠D = 120°
∴ ∠A = 128° and ∠D = 120 °.
Types of Quadrilaterals
S No. Quadrilateral Property Image 1. Kite a. No Parallel Sides
b. Two pairs of adjacent sides are equal.2. Trapezium One pair of opposite sides is parallel. 3. Parallelogram Both pairs of opposite sides are parallel. 3. Rectangle a. Both the pair of opposite sides are parallel.
b. Opposite sides are equal.c.
All the four angles are 90°.4. Square a. All four sides are equal.
b. Opposite sides are parallel.
c. All the four angles are 90°.5. Rhombus a. All four sides are equal.
b. Opposite sides are parallel.
c. Opposite angles are equal.d.
Diagonals intersect each other at the centre and at 90°.Remark: A square, Rectangle and Rhombus are also a parallelogram.
Properties of a Parallelogram
Theorem 1: When we divide a parallelogram into two parts diagonally then it divides it into two congruent triangles.
∆ABD ≅ ∆CDB
Theorem 2: In a parallelogram, opposite sides will always be equal.
Theorem 3: A quadrilateral will be a parallelogram if each pair of its opposite sides will be equal.
Here, AD = BC and AB = DC
Then ABCD is a parallelogram.
Theorem 4: In a parallelogram, opposite angles are equal.
In ABCD, ∠A = ∠C and ∠B = ∠D
Theorem 5: In a quadrilateral, if each pair of opposite angles is equal, then it is said to be a parallelogram. This is the reverse of Theorem 4.
Theorem 6: The diagonals of a parallelogram bisect each other.
Here, AC and BD are the diagonals of the parallelogram ABCD.
So the bisect each other at the centre.
DE = EB and AE = EC
Theorem 7: When the diagonals of the given quadrilateral bisect each other, then it is a parallelogram.
This is the reverse of the theorem 6.
The Mid-point Theorem
1. If a line segment joins the midpoints of the two sides of the triangle then it will be parallel to the third side of the triangle.
If AB = BC and CD = DE then BD ∥ AE.
2. If a line starts from the midpoint of one line and that line is parallel to the third line then it will intersect the midpoint of the third line.
If D is the midpoint of AB and DE∥ BC then E is the midpoint of AC.
Example
Prove that C is the midpoint of BF if ABFE is a trapezium and AB ∥ EF.D is the midpoint of AE and EF∥ DC.
Solution:
Let BE cut DC at a point G.
Now in ∆AEB, D is the midpoint of AE and DG ∥ AB.
By midpoint theorem, G is the midpoint of EB.
Again in ∆BEF, G is the midpoint of BE and GC∥ EF.
So, by midpoint theorem C is the midpoint of BF.
Hence proved.
Hindi Version Key Terms
Topic Terminology
Term
Important Tables
Table:
.
CIRCLES | Study
Mind Map Overal Idea Content Speed Notes Quick Coverage Introduction to Circles There are many objects in our life which are round in shape. A few examples are the clock, dart board, cartwheel, ring, Vehicle wheel, Coins, etc. (Scroll down to continue …)(Scroll down till end of the page) Study Tools Audio, Visual & Digital… readmore
Mind Map
Overal Idea
Content
Speed Notes
Quick Coverage
Introduction to Circles
There are many objects in our life which are round in shape. A few examples are the clock, dart board, cartwheel, ring, Vehicle wheel, Coins, etc. (Scroll down to continue …)(Scroll down till end of the page)
Study Tools
Audio, Visual & Digital Content
Circles
- Any closed shape with all points connected at equidistant from the centre forms a Circle.
- Any point which is equidistant from anywhere from its boundary is known as the Centre of the Circle.
- Radius is a Latin word which means ‘ray’ but in the circle it is the line segment from the centre of the circle to its edge. So any line starting or ending at the centre of the circle and joining anywhere on the border of the circle is known as the Radius of Circle.
Interior and Exterior of a Circle
In a flat surface, the interior of a circle is the line whose distance from the centre is less than the radius.
The exterior of a circle is the line in the plane whose distance from the centre is larger than the radius.
Terms related to circle
- Chord: Any straight line segment that’s both endpoints falls on the boundary of the circle is known as Chord. In Latin, it means ‘bowstring’.
- Diameter: Any straight line segment or Chord which passes through the centre of the Circle and its endpoints connects on the boundary of the Circle is known as the Diameter of Circle. So in a circle Diameter is the longest chord possible in a circle.
- Arc: Any smooth curve joining two points is known as Arc. So in Circle, we can have two possible Arcs, the bigger one is known as Major Arc and the smaller one is known as Minor Arc.
- Circumference: It is the length of the circle if we open and straighten it out to make a line segment.
Segment and Sector of the Circle
A segment of the circle is the region between either of its arcs and a chord. It could be a major or minor segment.
Sector of the circle is the area covered by an arc and two radii joining the centre of the circle. It could be the major or minor sector.
Angle Subtended by a Chord at a Point
If in a circle AB is the chord and is making ∠ACB at any point of the circle then this is the angle subtended by the chord AB at a point C.
Likewise, ∠AOB is the angle subtended by chord AB at point O i.e. at the centre and ∠ADB is also the angle subtended by AB at point D on the circle.
Theorem 1: Any two equal chords of a circle subtend equal angles at the centre.
Here in the circle, the two chords are given and PQ = RS with centre O.
So OP = OS = OQ = OR (all are radii of the circle)
∆POQ ≅ ∆SOR
∠POQ = ∠SOR
This shows that the angles subtended by equal chords to the centre are also equal.
Theorem 2: If the angles made by the chords of a circle at the centre are equal, then the chords must be equal.
This theorem is the reverse of the above Theorem 1.
Perpendicular from the Centre to a Chord
Theorem 3: If we draw a perpendicular from the centre of a circle to any chord then it bisects the chord.
If we draw a perpendicular from the centre to the chord of the circle then it will bisect the chord. And the bisector will make a 90° angle to the chord.
Theorem 4: The line which is drawn from the centre of a circle to bisect a chord must be perpendicular to the chord.
If we draw a line OB from the centre of the circle O to the midpoint of the chord AC i.e. B, then OB is the perpendicular to the chord AB.
If we join OA and OC, then
In ∆OBA and ∆OBC,
AB = BC (B is the midpoint of AC)
OA = OC (Both are the radii of the same circle)
OB = OB (same side)
Hence, ΔOBA ≅ ΔOBC (both are congruent by SSS congruence rule)
⇒ ∠OBA = ∠OBC (respective angles of congruent triangles)
∠OBA + ∠OBC = ∠ABC = 180° [Linear pair]
∠OBC + ∠OBC = 180° [Since ∠OBA = ∠OBC]
2 x ∠OBC = 180°
∠OBC = 90o
∠OBC = ∠OBA = 90°
∴ OB ⊥ AC
Circle through Three Points
Theorem 5: There is one and only one circle passing through three given non-collinear points.
In this figure, we have three non-collinear points A, B and C. Let us join AB and BC and then make the perpendicular bisector of both so that RS and PQ the perpendicular bisector of AB and BC respectively meet each other at Point O.
Now take the O as centre and OA as the radius to draw the circle which passes through the three points A, B and C.
This circle is known as Circumcircle. Its centre and radius are known as the Circumcenter and Circumradius.
Equal Chords and Their Distances from the Centre
Theorem 6: Two equal chords of a circle are at equal distance from the centre.
AB and CD are the two equal chords in the circle. If we draw the perpendicular bisector of these chords then the line segment from the centre to the chord is the distance of the chord from the centre.
If the chords are of equal size then their distance from the centre will also be equal.
Theorem 7: Chords at equal distance from the centre of a circle are also equal in length. This is the reverse of the above theorem which says that if the distance between the centre and the chords are equal then they must be of equal length.
Angle Subtended by an Arc of a Circle
The angle made by two different equal arcs to the centre of the circle will also be equal.
There are two arcs in the circle AB and CD which are equal in length.
So ∠AOB = ∠COD.
Theorem 8: The angle subtended by an arc at the centre is twice the angle subtended by the same arc at some other point on the remaining part of the circle.
In the above figure ∠POQ = 2∠PRQ.
Theorem 9: Angles from a common chord which are on the same segment of a circle are always equal.
If there are two angles subtended from a chord to any point on the circle which are on the same segment of the circle then they will be equal.
∠a = (1/2) ∠c (By theorem 8)
∠b = (1/2) ∠c
∠a = ∠b
Cyclic Quadrilaterals
If all the vertices of the quadrilateral come in a circle then it is said to be a cyclic quadrilateral.
Theorem 10: Any pair of opposite angles of a cyclic quadrilateral has the sum of 180º.
∠A + ∠B + ∠C + ∠D = 360º (angle sum property of a quadrilateral)
∠A + ∠C = 180°
∠B + ∠D = 180º
Theorem 11: If the pair of opposite angles of a quadrilateral has a sum of 180º, then the quadrilateral will be cyclic.
This is the reverse of the above theorem.
Hindi Version Key Terms
Topic Terminology
Term
Important Tables
Table:
.
HERON’S FORMULA | Study
Mind Map Overal Idea Content Speed Notes Quick Coverage Perimeter Perimeter is defined as the outside boundary of any closed shape. To calculate the perimeter of a given shape we need to add all the sides of the shape. Example: The perimeter of a rectangle is the sum of its all four sides. The unit… readmore
Mind Map
Overal Idea
Content
Speed Notes
Quick Coverage
Perimeter
Perimeter is defined as the outside boundary of any closed shape.
To calculate the perimeter of a given shape we need to add all the sides of the shape.
Example: The perimeter of a rectangle is the sum of its all four sides. The unit of the perimeter is the same as its length.
Perimeter of the Given rectangle = 3 + 7 + 3 + 7 cm
Perimeter of rectangle = 20 cm. (Scroll down till end of the page)
Study Tools
Audio, Visual & Digital Content
Area
Area of any closed figure is the surface enclosed by the perimeter. Unit of Area is the square of the unit of length.
Area of a triangle
The general formula to find the area of a triangle, if the height is given, is
Area of a Right Angled Triangle
To find the area of a right-angled triangle, we use the formula:
right-angled triangle, we take the two sides having the right angle, one as the base and one as height.
Example: Calculate area of a triangle of the Figure.
Data: base = 3 cm and height = 4 cm
Formula: Area of triangle = 1/2 × 3 × 4= 6 cm 2
Result: Area of a triangle of the Figure is 6 cm 2 .
Remark: If you take base as 4 cm and height as 3 cm then also the area of the triangle will remain the same.
Area of Equilateral Triangle
Equilateral Triangle: Equilateral Triangle is defined as a triangle having three equal sides.
To calculate the area of the Equilateral Triangle ABC,
We calculate the height (altitude), AD by making the median of the triangle.
In the given example, the Height (altitude), AD touches Base of the equilateral triangle at the midpoint of BC, Say point, D.
Here the equilateral triangle ABC has three equal sides, such as:
AB = BC = AC = 10 cm.
Since, midpoint of BC divides the triangle into two right angle triangles.
The height, AD, is calculated using Pythagoras theorem.
According to Pythagoras theorem, AB2 = AD2 + BD2
On substituting the values we get,
(10)2 = AD2 + (5)2
AD2 = (10)2 – (5)2
AD2 = 100 – 25 = 75
AD = 5√3
Now we can find the area of the triangle using the formula:
Area of triangle = 1/2 × base × height
On substituting the values we get,
Area of triangle = 1/2 × 10 × 5√3
25√3 cm2
Area of Isosceles Triangle
In the isosceles triangle also we need to find the height of the triangle then calculate the area of the triangle.
Here,
Area of a Triangle — by Heron’s Formula
The formula of the area of a triangle given by herons is called Heron’s Formula.
Heron’s Formula:
where a, b and c are the sides of the triangle and s is the semiperimeter
Generally, this formula is used when the height of the triangle is not possible to find or you can say if the triangle is a scalene triangle.
Here the sides of triangle are
AB = 12 cm
BC = 14 cm
AC = 6 cm
Application of Heron’s Formula in Finding Areas of Quadrilaterals
If we know the sides and one diagonal of the quadrilateral then we can find its area by using the Heron’s formula.
Find the area of the quadrilateral if its sides and the diagonal are given as follows.
Given, the sides of the quadrilateral
AB = 9 cm
BC = 40 cm
DC = 28 cm
AD = 15 cm
Diagonal is AC = 41 cm
Here, ∆ABC is a right angle triangle, so its area will be
Area of Quadrilateral ABCD = Area of ∆ABC + Area of ∆ADC
= 180 cm2 + 126 cm2
= 306 cm2
Hindi Version Key Terms
Topic Terminology
Term
Important Tables
Table:
.
Integers | Assess
Assessment Tools
Assign | Assess | Analyse
Quick Quiz
Objective Assessment
Question Bank
List Of Questions With Key, Aswers & Solutions
Back To Learn
Re – Learn
Go Back To Learn Again
The Triangle and its Properties | Assess
Assessment Tools
Assign | Assess | Analyse
Quick Quiz
Objective Assessment
Question Bank
List Of Questions With Key, Aswers & Solutions
Back To Learn
Re – Learn
Go Back To Learn Again
Comparing Quantities | Assess
Assessment Tools
Assign | Assess | Analyse
Quick Quiz
Objective Assessment
Question Bank
List Of Questions With Key, Aswers & Solutions
Back To Learn
Re – Learn
Go Back To Learn Again
Rational Numbers | Assess
Assessment Tools
Assign | Assess | Analyse
Quick Quiz
Objective Assessment
Question Bank
List Of Questions With Key, Aswers & Solutions
Back To Learn
Re – Learn
Go Back To Learn Again
Simple Equations | Assess
Assessment Tools
Assign | Assess | Analyse
Quick Quiz
Objective Assessment
Question Bank
List Of Questions With Key, Aswers & Solutions
Back To Learn
Re – Learn
Go Back To Learn Again
Lines and Angles | Assess
Assessment Tools
Assign | Assess | Analyse
Quick Quiz
Objective Assessment
Question Bank
List Of Questions With Key, Aswers & Solutions
Back To Learn
Re – Learn
Go Back To Learn Again
Perimeter and Area | Assess
Assessment Tools
Assign | Assess | Analyse
Quick Quiz
Objective Assessment
Question Bank
List Of Questions With Key, Aswers & Solutions
Back To Learn
Re – Learn
Go Back To Learn Again
Algebraic Expressions | Assess
Assessment Tools
Assign | Assess | Analyse
Quick Quiz
Objective Assessment
Question Bank
List Of Questions With Key, Aswers & Solutions
Back To Learn
Re – Learn
Go Back To Learn Again
Exponents and Powers | Assess
Assessment Tools
Assign | Assess | Analyse
Quick Quiz
Objective Assessment
Question Bank
List Of Questions With Key, Aswers & Solutions
Back To Learn
Re – Learn
Go Back To Learn Again
Symmetry | Assess
Assessment Tools
Assign | Assess | Analyse
Quick Quiz
Objective Assessment
Question Bank
List Of Questions With Key, Aswers & Solutions
Back To Learn
Re – Learn
Go Back To Learn Again
Visualising Solid Shapes | Assess
Assessment Tools
Assign | Assess | Analyse
Quick Quiz
Objective Assessment
Question Bank
List Of Questions With Key, Aswers & Solutions
Back To Learn
Re – Learn
Go Back To Learn Again
Nutrition in Plants | Assess
Assessment Tools
Assign | Assess | Analyse
Quick Quiz
Objective Assessment
Question Bank
List Of Questions With Key, Aswers & Solutions
Back To Learn
Re – Learn
Go Back To Learn Again
Nutrition in Animals | Assess
Assessment Tools
Assign | Assess | Analyse
Quick Quiz
Objective Assessment
Question Bank
List Of Questions With Key, Aswers & Solutions
Back To Learn
Re – Learn
Go Back To Learn Again
Heat | Assess
Assessment Tools
Assign | Assess | Analyse
Quick Quiz
Objective Assessment
Question Bank
List Of Questions With Key, Aswers & Solutions
Back To Learn
Re – Learn
Go Back To Learn Again
Acids, Bases and Salts | Assess
Assessment Tools
Assign | Assess | Analyse
Quick Quiz
Objective Assessment
Question Bank
List Of Questions With Key, Aswers & Solutions
Back To Learn
Re – Learn
Go Back To Learn Again