Ratio and ProportionComparison By Taking Difference | Speed Notes
Notes For Quick Recap
CHAPTER 12Ratio and ProportionComparison by taking difference: For comparing quantities of thesame type, wecommonly use themethod of taking difference between thequantities. Some times thecomparison by difference does not makebetter sense thanthe comparison by division. (Scroll down to continue)
Study Tools
Audio, Visual & Digital Content
Comparison by Division: In many situations, a more meaningful comparison between quantities is made byusing division, i.e.. by seeing how many times one quantity is to the other quantity. This method is known ascomparison by ratio. The comparison of two numbers or quantities bydivision is knownas the ratio. Symbol ‘:’is used todenote ratio. For comparison by ratio, thetwo quantities mustbe in thesame unit. Ifthey are not,they should beexpressed in thesame unit before the ratio istaken. For example, Isha’s weight is25 kg andher father’s weight is 75 kg.We say thatIsha’s father’s weight and Isha’s weight are in theratio 3 : 1
Hindi Version
Dig Deep
Topic Level Resources
Sub – Topics
Select A Topic
Topic:
Chapters Index
Select Another Chapter
[display-posts category=”CBSE 6 – Mathematics – Study – Premium” posts_per_page=”25″]
Whole Numbers The numbers 1,2, 3, ……which we use for counting are known as natural numbers. If you add 1 to a natural number, we get its successor. If you subtract 1 from a natural number, you get its predecessor. (Scroll down to continue …)
Study Tools
Audio, Visual & Digital Content
Every natural number has a successor. Every natural number except 1 has a predecessor.
Whole Numbers
Whole numbers are formed by adding zero to the collection of natural numbers. Hence, the set of whole numbers includes 0, 1, 2, 3, and so on.
Key Properties of Whole Numbers:
Successors and Predecessors:
Every whole number has a successor. For example:
The successor of 0 is 1.
The successor of 1 is 2.
The successor of 2 is 3.
Every whole number except zero has a predecessor. For example:
The predecessor of 1 is 0.
The predecessor of 2 is 1.
The predecessor of 3 is 2.
Relationship with Natural Numbers:
All natural numbers (1, 2, 3, …) are whole numbers, but not all whole numbers are natural numbers since whole numbers include 0.
Number Line Representation:
Whole Number Line
To visualize whole numbers, we can draw a number line starting from 0:
Mark points at equal intervals to the right: 0, 1, 2, 3, …
This number line allows us to carry out operations:
Addition: Moving to the right (e.g., 1 + 2 = 3).
Subtraction: Moving to the left (e.g., 3 – 1 = 2).
Multiplication: Making equal jumps (e.g., 2 × 3 means jumping twice the distance of 2, reaching 6).
Division: Although division can be tricky, it involves partitioning. For example, 6 ÷ 2 means splitting 6 into 2 equal parts, resulting in 3.
Closure Properties:
Adding two whole numbers always results in a whole number:
Examples:
2 + 3 = 5
0 + 4 = 4
1 + 1 = 2
Multiplying two whole numbers also results in a whole number:
Examples:
2 × 3 = 6
0 × 5 = 0
1 × 4 = 4
Whole numbers are closed under subtraction only if the result is non-negative:
Examples:
2 – 1 = 1
5 – 3 = 2
3 – 3 = 0
Yet, if the result is negative, they are not closed under subtraction:
Example: 2 – 3 = -1 (not a whole number).
So, the whole numbers are not not closed under subtraction.
Division by whole numbers is defined only when the divisor is not zero, and the result is a whole number:
Examples:
6 ÷ 2 = 3
8 ÷ 4 = 2
0 ÷ 5 = 0
Division by zero is undefined (e.g., 5 ÷ 0).
So, the whole numbers are not not closed under division.
Identity Elements:
Zero acts as the identity for addition:
Example: 5 + 0 = 5.
The whole number 1 acts as the identity for multiplication:
Example: 3 × 1 = 3.
Commutative and Associative Properties:
Addition is commutative:
Examples:
2 + 3 = 3 + 2
1 + 4 = 4 + 1
0 + 5 = 5 + 0
Multiplication is also commutative:
Examples:
2 × 3 = 3 × 2
1 × 4 = 4 × 1
0 × 5 = 5 × 0
Both addition and multiplication are associative:
Examples for addition:
(1 + 2) + 3 = 1 + (2 + 3)
(0 + 4) + 1 = 0 + (4 + 1)
(2 + 2) + 2 = 2 + (2 + 2)
Examples for multiplication:
(1 × 2) × 3 = 1 × (2 × 3)
(0 × 4) × 1 = 0 × (4 × 1)
(2 × 2) × 2 = 2 × (2 × 2)
Distributive Property:
Multiplication distributes over addition:
Example: 2 × (3 + 4) = 2 × 3 + 2 × 4.
Understanding these properties helps simplify calculations. It enhances our grasp of numerical patterns. These patterns are not only interesting but also practical for mental math.
Hindi Version
Dig Deep
Topic Level Resources
Sub – Topics
Select A Topic
Topic:
Chapters Index
Select Another Chapter
[display-posts category=”CBSE 6 – Mathematics – Study – Premium” posts_per_page=”25″]
We have discussed multiples, divisors, factors and have seenhow to identify factors and multiples. We have discussed and discovered thefollowing: (a) A factor of a number is an exactdivisor of thatnumber. (Scroll down to continue …)
Study Tools
Audio, Visual & Digital Content
(b) Every number is a factor of itself. 1 is a factor ofevery number.
(c) Every factor ofa number isless than or equal tothe given number.
(d) Every number isa multiple ofeach of itsfactors.
(e) Every multiple ofa given number is greater thanor equal tothat number.
(f) Every number is a multiple of itself.
We have learnt that – (a) The number otherthan 1, withonly factors namely 1 and thenumber itself, isa prime number. Numbers that have more than two factors are called composite numbers. Number 1is neither prime nor composite.
(b) The number 2is the smallest prime number andis even. Every prime number other than 2 isodd.
(c) Two numbers withonly 1 asa common factor are called co-prime numbers.
(d) If a number is divisible byanother number thenit is divisible by each of the factors of that number.
(e) A number divisible by two co-prime numbers is divisible by their product also.
We have discussed how we can find just by looking at a number, whether it is divisible by small numbers 2,3,4,5,8,9 and 11.
We have explored the relationship between digits of thenumbers and theirdivisibility by different numbers.
(a) Divisibility by 2,5and 10 canbe seen byjust the lastdigit.
(b) Divisibility by 3and 9 ischecked by finding the sum ofall digits.
(c) Divisibility by 4 and 8is checked bythe last 2and 3 digits respectively.
(d) Divisibility of11 is checked by comparing thesum of digits at odd andeven places.
We have discovered that if twonumbers are divisible by a number then their sum and difference are also divisible by that number.
We have learnt that – (a) The Highest Common Factor (HCF) of two ormore given numbers is the highest of their common factors.
(b) The Lowest Common Multiple (LCM) of two ormore given numbers is the lowest of their common multiples.
Hindi Version
Dig Deep
Topic Level Resources
Sub – Topics
Select A Topic
Topic:
Chapters Index
Select Another Chapter
[display-posts category=”CBSE 6 – Mathematics – Study – Premium” posts_per_page=”25″]
Geometry is a branch of mathematics concerned with properties of space such as the distance, shape, size, and relative position of figures. A mathematician who works in the field of geometry is called a 🎉geometer. (Scroll down to continue …)
Study Tools
Audio, Visual & Digital Content
Basic Geometrical Ideas | Speed Notes
Notes For Quick Recap
Geometry
Geometry is a branch of mathematics concerned with properties of space such as the distance, shape, size, and relative position of figures. A mathematician who works in the field of geometry is called a 🎉geometer.
Space
Space: space refers to a set of points that form a particular type of structure.
Plane
A plane is a flat surface that extends infinitely in all directions
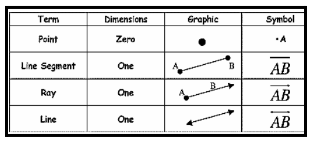
Point
Point is an exact position or location in space with no dimensions.
Mathematically, a point is defined as a circle with zero radius.
Since it is not possible its is represented by a very small dot.
A point is usually represented by a capital letter.
In mathematical terms, pont is a cirlce with no radius. It does mean that a very very small circle.
A point determines a location. It is usually denoted by a capital letter.
Lines And Its Types
Ray
A Ray is a straight path that stars at a point and extends infinitely in one direction.
Note: A ray is a portion of line starting at a point and extends in one direction endlessly. A ray has only one endpoint (Initial point).
Line or Straight Line
A line is a straight path that extends infinitely in two opposite directions. It can be treated as a combination of two rays starting from the same point but extending in the opposite directions.
Note: A line has no end points.
Line Segment:
A line segment is the part of a line between two points. (Segment means part).
The length of a line segment is the shortest length between two end points.
The line segment has two end points. Note: A line Segment has two endpoints. (both Initial and end points). (Scroll down to continue …).
Intersecting Lines and Non-intersecting Lines
Intersecting And Parallel Lines
Parallel Lines
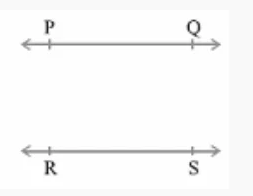
The lines which never cross each other at any point are called Parallel lines or Non-intersecting lines.
In other words, lines that are always the same distance apart from each other and that never meet are called Parallel lines Or Non-intersecting lines.
The perpendicular length between two lines is the distance between parallel lines.
Note: Parallel lines do not have any common point.
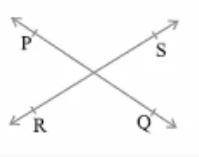
Intersecting Lines
The lines which cross (meet) each other at a point are called Intersecting Lines or non-parallel lines.
Intersecting lines meet at only one point.
Angle
An angle is made up of two rays starting from a common end point.
An angle leads to three divisions of a region:
On the angle, the interior of the angle and the exterior of the angle.
Curve
In geometry, a curve is a line or shape that is drawn smoothly and continuously in a plane with bends or turns.
In other words, Curve is a drawing (straight or non-straight) made without lifting the pencil may be called a curve.
Mathematicians define a curve as any shape that can be drawn without lifting the pen.
In Mathematics, A curve is a continuous and smooth line that is defined by a mathematical function or parametric equations.
Note: In this sense, a line is also a curve.
Types of Curves
Simple Or Open And Closed Curves
Cureves are two types based on intersection (crossing). They are (i) Simple or Open curve (ii) Closed curve.
Simple Curve
Simple or open curve is a curve that does not cross (intersect) itself.
Closed Curve
Closed curve is a curve that crosses (intersects) itself.
Concave And Convex Curves
Curves are of two types. They are concave curve and convex curve.
Concave Curve:
A curve is concave is a curve that curves inward, resembling a cave.
Examples:
– The interior of a circle.
– The graph of a concave function like y = -x2.
Convex Curves:
A curve is convex if it curves outward.
Examples:
– The exterior of a circle.
– The graph of a convex function like y = x2.
Polygon
A polygon is a simple closed figure formed by the line segments.
Types of Polygons
Polygons are classified into two types on the basis of interior angles: as (i) Convex polygon (ii) Concave polygon.
(a) Concave Polygon:
A concave polygon is a simple polygon that has at least one interior angle, that is greater than 1800 and less than 3600 (Reflex angle).
And at Least one diagonal lies outside of the closed figure.
Atlest one diagonal lies outside of the polygon.
b. Convex Polygon:
A convex polygon is a simple polygon that has at least no interior angle that is greater than 1800 and less than 3600 (Reflex angle).
And no diagonal lies outside of the closed figure.
In this case, the angles are either acute or obtuse (angle < 180 o).
Regular And Irregular Polygon
On the basis of sides, there are two types of polygons as Regular Polygon and Irregular Polygon
(a) Regular Polygon:
A convex polygon is called a regular polygon, if all its sides and angles are equal as shown in the following figures.
Each angle of a regular polygon of n-sides =
Part of Polygon
(i) Sides Of The Polygon
The line segments of a polygone are called sides of the polygon.
(ii) Adjacent Sides Of Polygon
Adjacent sides of a polygon are thesides of a polygon with a common end point.
(iii) Vertex Of Polygon
Vertext of a polygon is a point at which a pair of sides meet.
(iv) Adjacent Vertices
Adjacent vertices of polygon are the end points of the same side of the polygon.
(v) diagonal
Diagonal of a polygone is a line segment that joins the non-adjacent vertices of the polygon.
Triangle
A triangle is a three-sided polygon.
In other terms triangle is a three sided closed figure.
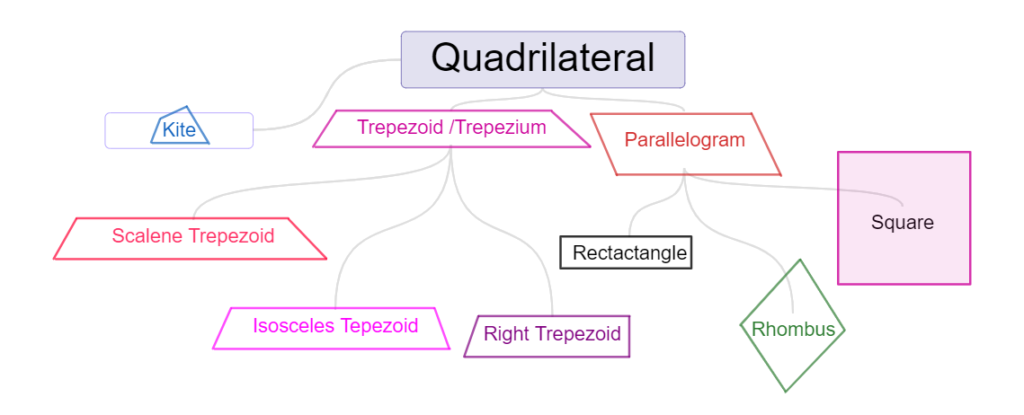
Quadrilateral
A quadrilateral is a four-sided polygon. (It shouldbe named cyclically).
In any
similar relations exist for the other three angles.
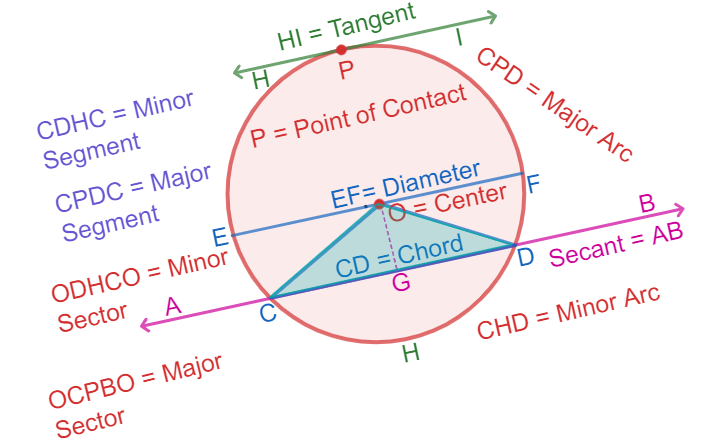
Circle And Its Parts
A circle is the path of a point moving at the same distance from a fixed point.
Centre Of Circle
Centre Of Circle is a point that is equidistant from any point on the boundary of the circle.
In other words the centre of the circles is a centre point of the circle.
Radius Of Circle
Radius of circle is the distance between the centre of the circle and any point on the boundary of the circle.
Circumference Of Circle
Circumference of circle is the length of the boundary of the circle.
Chord Of Circle
A chord of a circle is a line segment joining any two points on the circle.
A diameter is a chord passing throughthe Centre of the circle.
Sector Of Circle
A sector is the region in the interior of a circle enclosed by an arc on one side and a pair of radii on the other two sides.
Segment Of Circle
A segment of a circle is a region in the interior of the circle enclosed by an arc and a chord.
The diameter of a circle divides it into two semi-circles.
The diameter of a circle divides it into two semi-circles.
Hindi Version
Dig Deep
Topic Level Resources
Sub – Topics
Select A Topic
Topic:
Chapters Index
Select Another Chapter
[display-posts category=”CBSE 6 – Mathematics – Study – Premium” posts_per_page=”25″]
The distance betweenthe end pointsof a line segment is its length. A graduatedruler and the divider are useful to compare lengthsof line segments. When a hand of a clock moves from one position to another position we have an examplefor an angle. (Scroll down to continue …)
Study Tools
Audio, Visual & Digital Content
One full turn of the hand is 1 revolution.
A right angle is ¼ revolution and a straight angle is ½ a revolution. We use a protractor to measure the size of an angle in degrees.
The measure of a right angle is 90° and hence that of a straight angle is 180°.
An angle is acute if its measure is smaller than that of a right angle and is obtuseif its measure is greaterthan that of a right angle and less than a straightangle.
A reflex angle is largerthan a straight angle.
Two intersecting lines are perpendicular if the anglebetween them is 90°.
The perpendicular bisector of a line segmentis a perpendicular to the line segmentthat divides it into two equal parts.
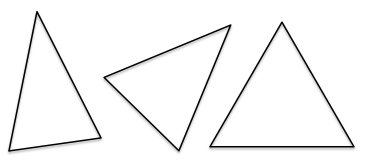
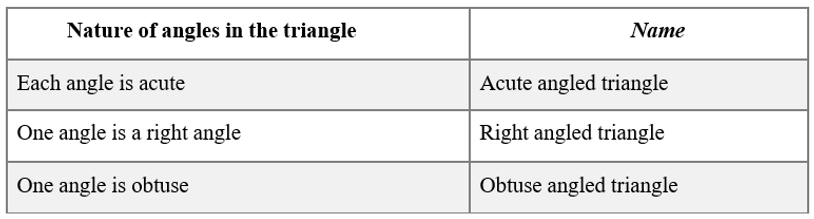
Triangles can be classified as follows based on their angles:
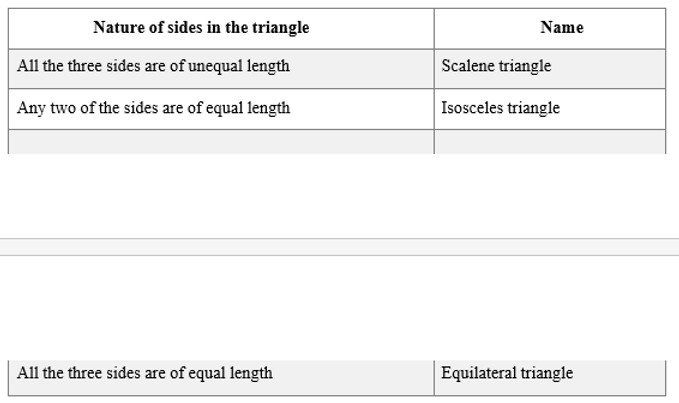
Triangles can be classified as follows based on the lengths of their sides:
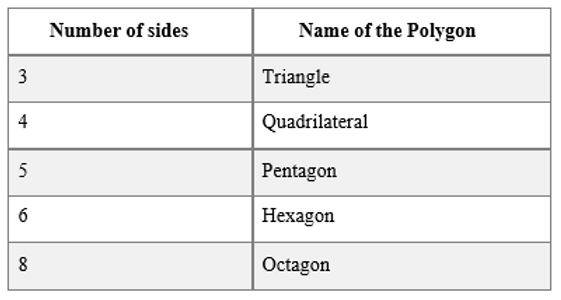
Polygons are namedbased on theirsides.
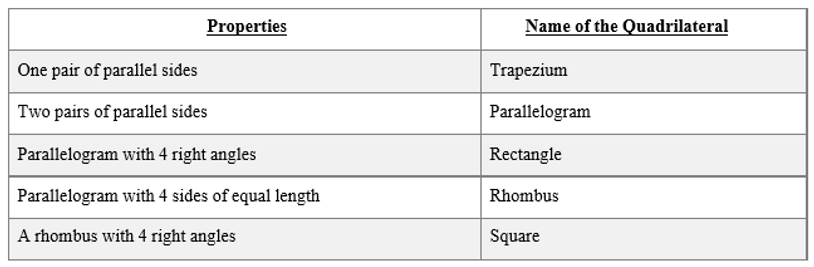
Quadrilaterals are furtherclassified with reference to their properties.
·We see aroundus many three dimensional shapes.Cubes, cuboids, spheres,
cylinders, cones,prisms and pyramidsare some of them.
Hindi Version
Dig Deep
Topic Level Resources
Sub – Topics
Select A Topic
Topic:
Chapters Index
Select Another Chapter
[display-posts category=”CBSE 6 – Mathematics – Study – Premium” posts_per_page=”25″]
