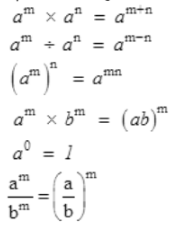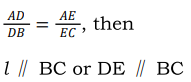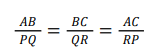Tag: English Version

Pre-Requisires

Test & Enrich

English Version

Lines And Angles | Speed Notes

Notes For Quick Recap

Basic Terms And Definitions

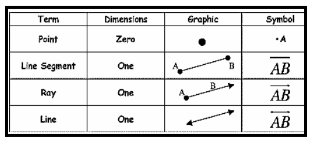
1. Point – A Point is that which has no component. It is represented by a dot.

A point is shown with a capital letter.

Examples: A, B, C …..

Colinear And Non-colinear Points

Collinear and Non-collinear points

5. Collinear points: Points lying on the same line are called Collinear Points.

Non-collinear points: Points which do not lie on the same line are called Non-Collinear Points.

Line – When we join two distinct points then we get a line. A line has no endpoints; it can be extended on both sides infinitely.

Line Segment Line – Segment is the part of the line which has two endpoints.

Ray – Ray is also a part of the line that has only one endpoint and has no end on the other side. (Scroll to continue …)

Study Tools

Audio, Visual & Digital Content

Lines And Their Types

Ray

A Ray is a straight path that stars at a point and extends infinitely in one direction.

Note: A ray is a portion of line starting at a point and extends in one direction endlessly. A ray has only one endpoint (Initial point).

Line or Straight Line

A line is a straight path that extends infinitely in two opposite directions. It can be treated as a combination of two rays starting from the same point but extending in the opposite directions.

Note: A line has no end points.

Line Segment:

A line segment is the part of a line between two points. (Segment means part).

The length of a line segment is the shortest length between two endpoints.

The line segment has two endpoints. Note: A line Segment has two endpoints. (both Initial and end points).

Intersecting Lines and Non-intersecting Lines

Intersecting Lines

Lines that meet or cross at a point with each other are called intersecting lines Or Non-parallel lines.

Intersecting lines meet at a point.

Parallel Lines

Lines that are always the same distance apart from each other and that never meet are called Parallel lines or Non-intersecting lines.

Note: Parallel lines do not have any common point.

Angles

When two rays begin from the same endpoint then they form an Angle. The two rays are the arms of the angle and the endpoint is the vertex of the angle.

Types of Angles By Measure

Complementary and Supplementary Angles

Complementary Angles are the different angles whose sum is 90°.

Suplementary Angles are the different angles whose sum is 180°

The sum of two adjacent angles formed by that ray is 180°

Angles Based On Position

Adjacent Angles: Two angles that share a common sideare called Adjacent Angles.

Linear Pair: A pair of adjacent angles whose non-common sides form a straight line (i.e., they are supplementary and add up to 180°).

Vertical (Opposite) Angles:

Angles opposite each other when two lines intersect. They are always equal.

Angles:

An angle is formed by two rays(called the sides or arms of the angle) with a common endpoint called the vertex.

Angles are measured in degrees(°) or radians, with a full rotation being 360°.

Special Angle Pairs:

Complementary Angles:

Two angles whose measures add up to 90°.

Supplementary Angles: Two angles whose measures add up to 180°

Angles in Polygons:

Interior Angles: Angles on the inside of a polygon. The sum of the interior angles of an n-sided polygon is \((n-2) \times 180°\).

Exterior Angles: Angles on the outside of a polygon. The sum of the exterior angles of any polygon is always 360°.

Angles Formed by Parallel Lines and Transversals:

When a transversal intersects two parallel lines, several angle pairs are formed:

Corresponding Angles: Angles in the same position relative to the two lines and the transversal. They are equal.

Alternate Interior Angles: Angles on opposite sides of the transversal and inside the parallel lines. They are equal.

Alternate Exterior Angles: Angles on opposite sides of the transversal and outside the parallel lines. They are equal.

– **Consecutive (Same-Side) Interior Angles:** Angles on the same side of the transversal and inside the parallel lines. They are supplementary.

Measuring Angles:

Protractor: A tool used to measure angles in degrees.

Radians: Another unit of angle measure. One full revolution (360°) is equal to \(2\pi\) radians.

Angle Relationships in Circles:

Central Angle: An angle whose vertex is the centre of the circle. The measure of a central angle is equal to the measure of the arc it intercepts.

Inscribed Angle: An angle whose vertex is on the circle and whose sides contain chords of the circle. The measure of an inscribed angle is half the measure of the intercepted arc.

Angles Formed by Tangents and Chords: The measure of the angle formed by a tangent and a chord through the point of contact is half the measure of the intercepted arc.

Angles Inside the Circle (but not at the centre): The measure of an angle formed by two intersecting chords is half the sum of the measures of the arcs intercepted by the angle and its vertical angle.

Trigonometric Angles:

Standard Position: An angle with its vertex at the origin and one side on the positive x-axis.

Reference Angle: The acute angle formed by the terminal side of an angle and the x-axis.

Quadrantal Angles: Angles that are multiples of 90° (0°, 90°, 180°, 270°, 360°).

Angle Conversions:

Degrees to Radians: Multiply the number of degrees by \(\frac{\pi}{180}\).

Radians to Degrees: Multiply the number of radians by \(\frac{180}{\pi}\).

Key Properties and Theorems:

Angle Sum Property of a Triangle:

The sum of the interior angles of a triangle is always 180°.

Exterior Angle Theorem:

The measure of an exterior angle of a triangle is equal to the sum of the measures of the two non-adjacent interior angles.

Polygon Interior Angles Theorem:

The sum of the interior angles of an n-sided polygon is \((n-2) \times 180°\).

Understanding these fundamental aspects of angles will enhance your comprehension of geometric principles and their applications.

Pairs of Angles Axioms

1. If a ray stands on a line, then the sum of two adjacent angles formed by that ray is 180°.

This shows that the common arm of the two angles is the ray which is standing on a line and the two adjacent angles are the linear pair of the angles. As the sum of two angles is 180° so these are supplementary angles too.

2. If the sum of two adjacent angles is 180°, then the arms which are not common of the angles form a line.

This is the reverse of the first axiom which says that the opposite is also true.

Vertically opposite Angles Theorem

When two lines intersect each other, then the vertically opposite angles so formed will be equal.

AC and BD are intersecting each other so ∠AOD = ∠BOC and ∠AOB = DOC.

Parallel Lines and a Transversal

If a line passes through two distinct lines and intersects them at distant points then this line is called Transversal Line.

Here line “l” is transversal of line m and n.

Exterior Angles – ∠1, ∠2, ∠7 and ∠8

Interior Angles – ∠3, ∠4, ∠5 and ∠6

Pairs of angles formed when a transversal intersects two lines-

1. Corresponding Angles:

∠ 1 and ∠ 5
∠ 2 and ∠ 6
∠ 4 and ∠ 8
∠ 3 and ∠ 7

2. Alternate Interior Angles:

∠ 4 and ∠ 6
∠ 3 and ∠ 5

3. Alternate Exterior Angles:

∠ 1 and ∠ 7
∠ 2 and ∠ 8

4. Interior Angles on the same side of the transversal:

∠ 4 and ∠ 5
∠ 3 and ∠ 6

Transversal Axioms

1. If a transversal intersects two parallel lines, then

Each pair of corresponding angles will be equal.
Each pair of alternate interior angles will be equal.
Each pair of interior angles on the same side of the transversal will be supplementary.

2. If a transversal intersects two lines in such a way that

Corresponding angles are equal then these two lines will be parallel to each other.
Alternate interior angles are equal then the two lines will be parallel.
Interior angles on the same side of the transversal are supplementary then the two lines will be parallel.

Lines Parallel To The Same Line

If two lines are parallel with a common line then these two lines will also be parallel to each other.

As in the above figure if AB ∥ CD and EF ∥ CD then AB ∥ EF.

Angle Sum Property of a Triangle

1. The sum of the angles of a triangle is 180º.

∠A + ∠B + ∠C = 180°

2. If we produce any side of a triangle, then the exterior angle formed is equal to the sum of the two interior opposite angles.

∠BCD = ∠BAC + ∠ABC.

Hindi Version

Dig Deep

Topic Level Resources

Sub – Topics

Select A Topic

Topic:

Chapters Index

Select Another Chapter

Assessments

Personalised Assessments

QUADRILATERALS | Study

Pre-Requisires

Test & Enrich

English Version

Quadrilaterals | Speed Notes

Notes For Quick Recap

Quadrilateral

Any closed polygon with four sides, four angles and four vertices are called Quadrilateral. It could be regular or irregular. (Sroll down to continute …)

Study Tools

Audio, Visual & Digital Content

Revision Notes – CBSE 09 Math – Quadrilaterals

Angle Sum Property of a Quadrilateral

The sum of the four angles of a quadrilateral is 360°

If we draw a diagonal in the quadrilateral, it divides it into two triangles.

And we know the angle sum property of a triangle i.e. the sum of all the three angles of a triangle is 180°.

The sum of angles of ∆ADC = 180°.

The sum of angles of ∆ABC = 180°.

By adding both we get ∠A + ∠B + ∠C + ∠D = 360°

Hence, the sum of the four angles of a quadrilateral is 360°.

Example

Find ∠A and ∠D, if BC∥ AD and ∠B = 52° and ∠C = 60° in the quadrilateral ABCD.

Solution:

Given BC ∥ AD, so ∠A and ∠B are consecutive interior angles.

So ∠A + ∠B = 180° (Sum of consecutive interior angles is 180°).

∠B = 52°

∠A = 180°- 52° = 128°

∠A + ∠B + ∠C + ∠D = 360° (Sum of the four angles of a quadrilateral is 360°).

∠C = 60°

128° + 52° + 60° + ∠D = 360°

∠D = 120°

∴ ∠A = 128° and ∠D = 120 °.

Types of Quadrilaterals

Remark: A square, Rectangle and Rhombus are also a parallelogram.

Properties of a Parallelogram

Theorem 1: When we divide a parallelogram into two parts diagonally then it divides it into two congruent triangles.

∆ABD ≅ ∆CDB

Theorem 2: In a parallelogram, opposite sides will always be equal.

Theorem 3: A quadrilateral will be a parallelogram if each pair of its opposite sides will be equal.

Here, AD = BC and AB = DC

Then ABCD is a parallelogram.

Theorem 4: In a parallelogram, opposite angles are equal.

In ABCD, ∠A = ∠C and ∠B = ∠D

Theorem 5: In a quadrilateral, if each pair of opposite angles is equal, then it is said to be a parallelogram. This is the reverse of Theorem 4.

Theorem 6: The diagonals of a parallelogram bisect each other.

Here, AC and BD are the diagonals of the parallelogram ABCD.

So the bisect each other at the centre.

DE = EB and AE = EC

Theorem 7: When the diagonals of the given quadrilateral bisect each other, then it is a parallelogram.

This is the reverse of the theorem 6.

The Mid-point Theorem

1. If a line segment joins the midpoints of the two sides of the triangle then it will be parallel to the third side of the triangle.

If AB = BC and CD = DE then BD ∥ AE.

2. If a line starts from the midpoint of one line and that line is parallel to the third line then it will intersect the midpoint of the third line.

If D is the midpoint of AB and DE∥ BC then E is the midpoint of AC.

Example

Prove that C is the midpoint of BF if ABFE is a trapezium and AB ∥ EF.D is the midpoint of AE and EF∥ DC.

Solution:

Let BE cut DC at a point G.

Now in ∆AEB, D is the midpoint of AE and DG ∥ AB.

By midpoint theorem, G is the midpoint of EB.

Again in ∆BEF, G is the midpoint of BE and GC∥ EF.

So, by midpoint theorem C is the midpoint of BF.

Hence proved.

Hindi Version

Dig Deep

Topic Level Resources

Sub – Topics

Select A Topic

Topic:

Chapters Index

Select Another Chapter

Assessments

Personalised Assessments

HERON’S FORMULA | Study
Assess
Interact
Pre-Requisires
Test & Enrich
Pre – Requisite

English Version
Heron’s Formula | Speed Notes
Notes For Quick Recap
Perimeter
Perimeter is defined as the outside boundary of any closed shape.
To calculate the perimeter of a given shape we need to add all the sides of the shape.
Example: The perimeter of a rectangle is the sum of its all four sides. The unit of the perimeter is the same as its length.
Perimeter of the Given rectangle = 3 + 7 + 3 + 7 cm
Perimeter of rectangle = 20 cm. (Scroll down to continue …)
Study Tools
Audio, Visual & Digital Content
Area
Area of any closed figure is the surface enclosed by the perimeter. Unit of Area is the square of the unit of length.
Area of a triangle
The general formula to find the area of a triangle, if the height is given, is
Area of a Right Angled Triangle
To find the area of a right-angled triangle, we use the formula:
right-angled triangle, we take the two sides having the right angle, one as the base and one as height.
Example: Calculate area of a triangle of the Figure.
Data: base = 3 cm and height = 4 cm
Formula: Area of triangle = 1/2 × 3 × 4= 6 cm²
Result: Area of a triangle of the Figure is 6 cm² .
Remark: If you take base as 4 cm and height as 3 cm then also the area of the triangle will remain the same.
Area of Equilateral Triangle
Equilateral Triangle: Equilateral Triangle is defined as a triangle having three equal sides.
To calculate the area of the Equilateral Triangle ABC,
We calculate the height (altitude), AD by making the median of the triangle.
In the given example, the Height (altitude), AD touches Base of the equilateral triangle at the midpoint of BC, Say point, D.
Here the equilateral triangle ABC has three equal sides, such as:
AB = BC = AC = 10 cm.
Since, midpoint of BC divides the triangle into two right angle triangles.
The height, AD, is calculated using Pythagoras theorem.
According to Pythagoras theorem, AB² = AD² + BD²
On substituting the values we get,
(10)² = AD² + (5)²
AD² = (10)² – (5)²
AD² = 100 – 25 = 75
AD = 5√3
Now we can find the area of the triangle using the formula:
Area of triangle = 1/2 × base × height
On substituting the values we get,
Area of triangle = 1/2 × 10 × 5√3
25√3 cm²
Area of Isosceles Triangle
In the isosceles triangle also we need to find the height of the triangle then calculate the area of the triangle.
Here,
Area of a Triangle — by Heron’s Formula
The formula of the area of a triangle given by herons is called Heron’s Formula.
Heron’s Formula:
where a, b and c are the sides of the triangle and s is the semiperimeter
Generally, this formula is used when the height of the triangle is not possible to find or you can say if the triangle is a scalene triangle.
Here the sides of triangle are
AB = 12 cm
BC = 14 cm
AC = 6 cm
Application of Heron’s Formula in Finding Areas of Quadrilaterals
If we know the sides and one diagonal of the quadrilateral then we can find its area by using the Heron’s formula.
Find the area of the quadrilateral if its sides and the diagonal are given as follows.
Given, the sides of the quadrilateral
AB = 9 cm
BC = 40 cm
DC = 28 cm
AD = 15 cm
Diagonal is AC = 41 cm
Here, ∆ABC is a right angle triangle, so its area will be
Area of Quadrilateral ABCD = Area of ∆ABC + Area of ∆ADC
= 180 cm² + 126 cm²
= 306 cm²

Hindi Version
Dig Deep
Topic Level Resources
Sub – Topics
Select A Topic
Topic:
Chapters Index
Select Another Chapter
Assessments
Personalised Assessments
Assess
November 5, 2023
INTRODUCTION TO EUCLID’S GEOMETRY | Study
Assess
Interact
Pre-Requisires
Test & Enrich
Pre – Requisite

English Version
Speed Notes
Notes For Quick Recap
Introduction to Euclid Geometry The necessity of geometry had been felt from ancient times in different parts of the world.
The practical problems faced by people of ancient civilization had developed this branch of mathematics.
Let us cite few examples.
With floods in the river, the demarcations of land owners on the river-side land were used to wipe out. (Scroll down to continue …)
Study Tools
Audio, Visual & Digital Content
In order to redraw the boundaries, the idea of area was introduced, the idea of area was introduced.
The volumes of granaries could be measured by using geometry.
The existence of Egyptian pyramids indicates the use of geometry from olden times.
In Vedic period, there was a manual of geometrical construction, known as Sulbasutra’s.
Different geometrical shapes were constructed as altars to perform various Vedic rites.
The word Geometry originates from the green word ‘Geo’ (earth) and metrein (to measure) Through Geometry was developed and applied from ancient time in various part the world, it was not presented in a systematic manner.
Later in 300 BC, the Egyptian mathematician Euclid, collected all the known work and arranged it in a systematic manner.
‘Elements’ is a classic treatise in geometry which was written by Euclid.
This was the most influential book. The ‘element’ was used as a text book for several years in western Europe.
The ‘elements’ started with 28 definitions, five postulates and five common notions and systematically built the rest of plane and solid geometry.
The geometrical approach given by Euclid is known as Euclid method.
The Euclid method consists of making a small set of assumptions and then proving many other proposition from these assumptions.
The assumptions, made were obvious universal truth. The two types of assumption, made were ‘axioms’ and ‘postulates’.
Euclid’s Definitions Euclid listed 23 definitions in book 1 of the ‘elements’.
We list a few of them: 1) 2) 3) 4) 5) 6) 7) A point is that which has no part A line is a breadth less length The ends of a line are points A straight line is a line which lies evenly with the points on itself. A surface is that which has length and breadth only.
The edges of a surface are lines A plane surface is surface which lies evenly with straight lines on its self. Starting with these definitions, Euclid assumed certain assumptions, known as axioms and postulates.
Euclid’s Axioms Axioms were assumptions which were used throughout mathematics and are not specifically linked to geometry.
Few of Euclid’s axioms are:
1) Things which are equal to the same thing are equal to one another.
2) It equals are added to equals; the wholes are equal.
3) 4) 5) 6) 7) If equals are subtracted from equals, the remainders are equal.
Things which coincide one another are equal to one another.
The whole is greater than the part Things which are double of the same thing are equal to one another.
Things which are half of the same things are equal to one another.
All these axioms refer to magnitude of same kind.
Axiom – 1 can be written as follows: If x = Z and y = Z, then x = y
Axiom – 2 explains the following: If x = y, then x + Z = y + Z According to axiom – 3, If x = y, then x – Z = y – Z Axiom – 4 justifies the principle of superposition that every thing equals itself.
Axiom – 5, gives us the concept of comparison. If x is a part of y, then there is a quantity Z such that x = y + Z or x > y Note that magnitudes of the same kind can be added, subtracted or compared.
Euclid’s Postulates Euclid used the term postulate for the assumptions that were specific to geometry. Euclid’s five postulates are as follows: Postulate 1: A straight line may be drawn from any one point to any other point. Same may be stated as axiom 5.1 Given two distinct points, there is a unique line that passes through them.
Postulate 2: A terminated line can be produced indefinitely. Postulate 3: A circle can be drawn with any centre and any radius. Postulate 4: All right angles are equal to one another. Postulate 5: If a straight line falling on two straight lines makes the interior angle on the same side of it taken together less than two right angles, then two straight lines, if produced indefinitely, meet on that side on which the sum of the angles is less than two right angles. Postulates 1 to Postulates 4 are very simple and obvious and therefore they are taken a ‘self evident truths’. Postulates 5 is complex and it needs to be discussed. Suppose the line XY falls on two lines AB and CD such that ∠1 + ∠2 < 180°, then the lines AB and CD will intersect at a point. In the given figure, they intersect on left side of PQ, if both are produced. Note: In mathematics the words axiom and postulate may be used interchangeably, though they have distinct meaning according to Euclid. System of Consistent Axioms A system of axioms is said to be consistent, if it is impossible to deduce a statement from these axioms, which contradicts any of the given axioms or proposition. Proposition or Theorem The statement or results which were proved by using Euclid’s axioms and postulates are called propositions or Theorems. Theorem: Two distinct lines cannot have more than one point in common. Proof: Given: AB and CD are two lines. To prove: They intersect at one point or they do not intersect. Proof: Suppose the lines AB and CD intersect at two points P and Q. This implies the line AB passes through the points P and Q. Also the line CD passes through the points P and Q. This implies there are two lines which pass through two distinct point P and Q. But we know that one and only one line can pass through two distinct points. This axiom contradicts out assumption that two distinct lines can have more than one point in common. The lines AB and CD cannot pass through two distinct point P and Q. Equivalent Versions of Euclid’s Fifth Postulate The two different version of fifth postulate a) For every line l and for every point P not lying on l, there exist a unique line m passing through P and parallel to l. b) Two distinct intersecting lines cannot be parallel to the same line.

Hindi Version
Dig Deep
Topic Level Resources
Sub – Topics
Select A Topic
Topic:
Chapters Index
Select Another Chapter
Assessments
Personalised Assessments
Assess
November 5, 2023
NUMBER SYSTEMS | Study
Assess
Interact
Pre – Requisites
Test & Enrich
Pre – Requisite

English Version
Speed Notes
Notes For Quick Coverage
Introduction to Natural Numbers
Non-negative counting numbers excluding zero are called Natural Numbers.
N = 1, 2, 3, 4, 5, ……….
Whole Numbers
All natural numbers including zero are called Whole Numbers.
W = 0, 1, 2, 3, 4, 5, ……………. (Scroll down to continue …)
Study Tools
Audio, Visual & Digital Content
Integers
All natural numbers, negative numbers and 0, together are called Integers.
Z = – 3, – 2, – 1, 0, 1, 2, 3, 4, …………..
Rational Numbers
The number ‘a’ is called Rational if it can be written in the form of r/s where ‘r’ and ‘s’ are integers and s ≠ 0,
Q = 2/3, 3/5, etc. all are rational numbers.
How to find a rational number between two given numbers?
To find the rational number between two given numbers ‘a’ and ‘b’.
Example:
Find 2 rational numbers between 4 and 5.
Solution:
To find the rational number between 4 and 5
To find another number we will follow the same process again.
Hence the two rational numbers between 4 and 5 are 9/2 and 17/4.
Remark: There could be unlimited rational numbers between any two rational numbers.
Irrational Numbers
The number ‘a’ which can’t be written in the form of p/q is called irrational. Here, p and q are integers and q ≠ 0. You can say that the numbers which are not rational are called Irrational Numbers.
Example – √7, √11 etc.
Real Numbers
All numbers including both rational and irrational numbers are called Real Numbers.
R = – 2, – (2/3), 0, 3 and √2
Real Numbers And Their Decimal Expansions
1. Rational Numbers
If the rational number is in the form of a/b, then we can get two situations by dividing a by b.
a. If the remainder becomes zero
While dividing if we get zero as the remainder after some steps then the decimal expansion of such a number is called terminating.
Example:
7/8 = 0.875
b. If the remainder does not become zero
While dividing if the decimal expansion continues and not becomes zero then it is called non-terminating or repeating expansion.
Example:
1/3 = 0.3333….
Hence, the decimal expansion of rational numbers could be terminating or non-terminating recurring and vice-versa.
2. Irrational Numbers
If we do the decimal expansion of an irrational number then it would be non –terminating non-recurring and vice-versa. i. e. the remainder does not become zero and also not repeated.
Example:
π = 3.141592653589793238……
Representing Real Numbers on the Number Line
To represent the real numbers on the number line, we use the process of successive magnification. We visualise the numbers through a magnifying glass on the number line.
Example:
Step 1: The number lies between 4 and 5, so we divide it into 10 equal parts. Now for the first decimal place, we will mark the number between 4.2 and 4.3.
Step 2: Now we will divide it into 10 equal parts again. The second decimal place will be between 4.26 and 4.27.
Step 3: Now we will again divide it into 10 equal parts. The third decimal place will be between 4.262 and 4.263.
Step 4: By doing the same process again we will mark the point at 4.2626.
Operations on Real Numbers
1. The sum, difference, product and quotient of two rational numbers will be rational.
Example:
2. If we add or subtract a rational number with an irrational number then the outcome will be irrational.
Example:
If 5 is a rational number. √7 is an irrational number. Then, 5 + √7 and 5 – √7 are irrational numbers.
3. If we multiply a non-zero rational number with an irrational number, the outcome will be irrational. If we divide a non-zero rational number with an irrational number, the outcome will also be irrational.
Example:
If 7 is a rational number and √5 is an irrational number then 7√7 and 7/√5 are irrational numbers.
4. The sum, difference, product and quotient of two irrational numbers could be rational or irrational.
Example:
Finding Roots of a Positive Real Number ‘x’ geometrically and mark it on the Number Line
To find √x geometrically
1. First, mark the distance x unit from point A on the line. This ensures that AB equals x unit.
2. From B mark a point C with the distance of 1 unit, so that BC = 1 unit.
3. Take the midpoint of AC and mark it as O. Then take OC as the radius and draw a semicircle.
4. From the point B draw a perpendicular BD which intersects the semicircle at point D.
The length of BD = √x.
To mark the position of √x on the number line, we will take AC as the number line. B will be zero. So C is point 1 on the number line.
Now we will take B as the centre and BD as the radius. We will draw the arc on the number line at point E.
Now E is √x on the number line.
Identities Related to Square Roots
If p and q are two positive real numbers
Examples:
1. Simplify
We will use the identity
2. Simplify
We will use the identity
Rationalising the Denominator
Rationalising the denominator means to convert the denominator containing a square root term into a rational number. This is done by finding the equivalent fraction of the given fraction.
For which we can use the identities of the real numbers.
Example:
Rationalise the denominator of 7/(7- √3).
Solution:
We will use the identityhere.
Laws of Exponents for Real Numbers
If we have a and b as the base and m and n as the exponents, then
1. a^m × aⁿ =a^m+n
2. (a^m)ⁿ = a^mn
4. a^mb^m = (ab)^m
5.a⁰ = 1
6. a¹ = a
7. 1/aⁿ = a^-n
Let a > 0 be a real number and n a positive integer.
Let a > 0 be a real number. Let m and n be integers. They have no common factors other than 1. Also, n > 0. Then,
Example:
Simplify the expression (2x³y⁴) (3xy⁵)².
Solution:
Here we will use the law of exponents
a^m × aⁿ =a^m+n and (a^m)ⁿ = a^mn
(2x³y⁴)(3xy⁵)²
(2x³y⁴)(3 ² x ² y¹⁰)
18. x³. x². y⁴. y¹⁰
18. x³⁺². y⁴⁺¹⁰
18x⁵y¹⁴
Here’s a simple outline for an eBook on Real Numbers:
Title: Understanding Real Numbers: A Comprehensive Guide
Table of Contents
Introduction to Real Numbers
What are Numbers?
Introduction to Real Numbers
Why Are Real Numbers Important?
Classification of Numbers
Natural Numbers
Whole Numbers
Integers
Rational Numbers
Irrational Numbers
Properties of Real Numbers
Closure Property
Commutative Property
Associative Property
Distributive Property
Identity and Inverse Elements
The Real Number Line
Concept of Number Line
Plotting Real Numbers on the Number Line
Understanding Density of Real Numbers
Rational and Irrational Numbers
Definition of Rational Numbers
Properties of Rational Numbers
Definition of Irrational Numbers
Examples of Irrational Numbers (like √2, π, e)
Proving √2 is Irrational
Decimals and Real Numbers
Finite and Infinite Decimals
Terminating and Non-Terminating Decimals
Relationship between Decimals and Fractions
Operations on Real Numbers
Addition and Subtraction
Multiplication and Division
Operations with Decimals
Operations with Irrational Numbers
Absolute Value and Real Numbers
Definition of Absolute Value
Geometric Representation on the Number Line
Properties of Absolute Value
The Concept of Infinity
Understanding Infinite Sets
Limits and Real Numbers
Approaching Infinity on the Number Line
Applications of Real Numbers
In Geometry (Pythagorean Theorem)
In Calculus (Limits, Derivatives, and Integrals)
In Daily Life (Measurements, Finance, etc.)
Advanced Topics on Real Numbers
Real Numbers in Algebra
Real Numbers and Functions
Real Numbers and Continuity
Conclusion
Summary of Key Concepts
Importance of Mastering Real Numbers
How Real Numbers Apply to Higher Mathematics
Chapter 1: Introduction to Real Numbers
What Are Numbers?
Numbers are abstract symbols used to represent quantities. Throughout history, different types of numbers have been developed to address various mathematical problems.
Introduction to Real Numbers
Real numbers are all the numbers that can be found on the number line. This includes rational numbers (such as 5, -3, and 0.75) and irrational numbers (such as √2 and π). Together, they form the building blocks of modern mathematics.
Real numbers are used to measure continuous quantities like distance, time, and weight. They are integral to the concepts of calculus, physics, engineering, and many other fields.
Why Are Real Numbers Important?
Real numbers play a critical role in mathematics. They allow us to describe the size of objects, calculate areas and volumes, and express very large or very small values. Without real numbers, much of modern science and technology would not exist.
Chapter 2: Classification of Numbers
Natural Numbers
The set of natural numbers consists of counting numbers, such as 1, 2, 3, and so on. These are the simplest type of numbers and do not include zero.
Whole Numbers
Whole numbers are like natural numbers but also include zero. Thus, the set is {0, 1, 2, 3,…}.
Integers
Integers expand on whole numbers by including negative numbers. The set of integers is {…, -3, -2, -1, 0, 1, 2, 3,…}.
Rational Numbers
Rational numbers are numbers that can be expressed as a fraction of two integers (a/b), where b ≠ 0. Examples of rational numbers include 1/2, -4, and 0.75.
Irrational Numbers
Irrational numbers cannot be expressed as a fraction of two integers. Examples include √2, π, and e. These numbers have non-repeating, non-terminating decimal expansions.
Chapter 3: Properties of Real Numbers
Closure Property
The set of real numbers is closed under addition, subtraction, multiplication, and division (except division by zero). This means that the result of any of these operations on two real numbers will always yield another real number.
Commutative Property
For any two real numbers a and b:
Addition: a + b = b + a
Multiplication: a × b = b × a
Associative Property
For any three real numbers a, b, and c:
Addition: (a + b) + c = a + (b + c)
Multiplication: (a × b) × c = a × (b × c)
Distributive Property
The distributive property connects addition and multiplication:
a × (b + c) = (a × b) + (a × c)
Hindi Version
Dig Deep
Topic Level Resources
Sub – Topics
Select A Topic
Topic:
Chapters Index
Select Another Chapter
Assessments
Personalised Assessments
Assess
November 5, 2023
LINEAR EQUATIONS IN TWO VARIABLES | Study
Assess
Interact
Pre-Requisires
Test & Enrich
Pre – Requisite

English Version
Linear Equations in Two Variables | Speed Notes
Notes For Quick Recap
Linear Equations
The equation of a straight line is the linear equation. It could be in one variable or two variables.
Linear Equation in One Variable
The equation with one variable in it is known as a Linear Equation in One Variable. (Scroll down to continue …)
Study Tools
Audio, Visual & Digital Content
The general form for Linear Equation in One Variable is px + q = s, where p, q and s are real numbers and p ≠ 0.
Example:
x + 5 = 10
y – 3 = 19
These are called Linear Equations in One Variable because the highest degree of the variable is one.
Graph of the Linear Equation in One Variable
We can mark the point of the linear equation in one variable on the number line.
x = 2 can be marked on the number line as follows –
Graph of the Linear Equation in One Variable
Linear Equation in Two Variables
An equation with two variables is known as a Linear Equation in Two Variables. The general form of the linear equation in two variables is
ax + by + c = 0
where a and b are coefficients and c is the constant. a ≠ 0 and b ≠ 0.
Example
6x + 2y + 5 = 0, etc.
Slope Intercept form
Generally, the linear equation in two variables is written in the slope-intercept form as this is the easiest way to find the slope of the straight line while drawing the graph of it.
The slope-intercept form is y = mx+c
Where m represents the slope of the line.
and c tells the point of intersection of the line with the y-axis.
Remark: If b = 0 i.e. if the equation is y = mx then the line will pass through the origin as the y-intercept is zero.
Solution of a Linear Equation
There is only one solution in the linear equation in one variable but there are infinitely many solutions in the linear equation in two variables.
As there are two variables, the solution will be in the form of an ordered pair, i.e. (x, y).
The pair which satisfies the equation is the solution to that particular equation.
Example:
Find the solution for the equation 2x + y = 7.
Solution:
To calculate the solution of the given equation we will take x = 0
2(0) + y = 7
y = 7
Hence, one solution is (0, 7).
To find another solution we will take y = 0
2x + 0 = 7
x = 3.5
So another solution is (3.5, 0).
Graph of a Linear Equation in Two Variables
To draw the graph of a linear equation in two variables, we need to draw a table to write the solutions of the given equation, and then plot them on the Cartesian plane.
By joining these coordinates, we get the line of that equation.
The coordinates which satisfy the given Equation lie on the line of the equation.
Every point (x, y) on the line is the solution x = a, y = b of the given Equation.
Any point, which does not lie on the line AB, is not a solution of Equation.
Example:
Draw the graph of the equation 3x + 4y = 12.
Solution:
To draw the graph of the equation 3x + 4y = 12, we need to find the solutions of the equation.
Let x = 0
3(0) + 4y = 12
y = 3
Let y = 0
3x + 4(0) = 12
x = 4
Now draw a table to write the solutions.
x 0 4
y 3 0
Now we can draw the graph easily by plotting these points on the Cartesian plane.
Linear Equation in Two Variables
Equations of Lines Parallel to the x-axis and y-axis
When we draw the graph of the linear equation in one variable then it will be a point on the number line.
x – 5 = 0
x = 5
This shows that it has only one solution i.e. x = 5, so it can be plotted on the number line.
But if we treat this equation as the linear equation in two variables then it will have infinitely many solutions and the graph will be a straight line.
x – 5 = 0 or x + (0) y – 5 = 0
This shows that this is the linear equation in two variables where the value of y is always zero. So the line will not touch the y-axis at any point.
x = 5, x = number, then the graph will be the vertical line parallel to the y-axis.
All the points on the line will be the solution of the given equation.
Equations of Lines Parallel to the x-axis and y-axis
Similarly if y = – 3, y = number then the graph will be the horizontal line parallel to the x-axis.

Hindi Version
Dig Deep
Topic Level Resources
Sub – Topics
Select A Topic
Topic:
Chapters Index
Select Another Chapter
Assessments
Personalised Assessments
Assess
November 5, 2023
COORDINATE GEOMETRY | Study
Assess
Interact
Pre-Requisires
Test & Enrich
Pre – Requisite

English Version
Coordinate Geometry: Cartesian Plane | Speed Notes
Notes For Quick Recap
Cartesian System
A plane formed by two number lines, one horizontal
and the other vertical, such that they intersect each
other at their zeroes, and then they form a Cartesian
Plane.
Scroll Down To Continue …
Study Tools
Audio, Visual & Digital Content
● The horizontal line is known as the x-axis and the vertical line is known
as the y-axis.
● The point where these two lines intersect each other is called the origin.
It is represented as ‘O’.
● OX and OY are the positive directions as the positive numbers lie in the
right and upward direction.
● Similarly, the left and the downward directions are the negative directions
as all the negative numbers lie there.
Quadrants of the Cartesian Plane The Cartesian plane is divided into four quadrants namely Quadrant I, Quadrant II, Quadrant III, and Quadrant IV anticlockwise from OX.
Coordinates of a Point To write the coordinates of a point we need to follow the following rules. ● Thex – coordinate of a point is marked by drawing perpendicular from the y-axis measured a length of the x-axis .It is also called the Abscissa.
They – coordinate of a point is marked by drawing a perpendicular from the x-axis measured a length of the y-axis .It is also called the Ordinate. ● While writing the coordinates of a point in the coordinate plane, the x – coordinate comes first, and then the y – coordinate. We write the coordinates in brackets. In figure, OB = CA = x coordinate (Abscissa), and CO = AB = y coordinate (Ordinate). We write the coordinate as (x, y).
Remarks:
As the origin, O has zero distance from the x-axis and the y-axis so its abscissa and ordinate are zero. Hence the coordinate of the origin is (0, 0). The relationship between the signs of the coordinates of a point and the quadrant of a point in which it lies.
Plotting a Point in the Plane if its Coordinates are Given
Steps to plot the point (2, 3) on the Cartesian plane:
● First of all, we need to draw the Cartesian plane by drawing the coordinate axes with 1 unit = 1 cm.
● To mark the x coordinates, starting from 0 moves towards the positive x-axis and counts to 2.
● To mark the y coordinate, starting from 2 moves upwards in the positive direction and counts to 3.
● Now this point is the coordinate (2, 3). Likewise, we can plot all the other points, like (-3, 1) and (-1.5,-2.5) in the figure.
Question: Are the coordinates (x, y) = (y, x)? Let x = (-4) and y = (-2) So (x, y) = (- 4, – 2) (y, x) = (- 2, – 4)
Let’s mark these coordinates on the Cartesian plane. You can see that the positions of both the points are different in the Cartesian plane. So, If x ≠ y, then (x, y) ≠ (y, x), and (x, y) = (y, x), if x = y.
Example: Plot the points (6, 4), (- 6,- 4), (- 6, 4) and (6,- 4) on the Cartesian plane.
Solution: Since both numbers 6, 4 are positive the point (6, 4) lies in the first quadrant. For x coordinate, we will move towards the right and count to 6. Then from that point go upward and count to 4. Mark that point as the coordinate (6, 4). Similarly, we can plot all the other three points.

Hindi Version
Dig Deep
Topic Level Resources
Sub – Topics
Select A Topic
Topic:
Chapters Index
Select Another Chapter
Assessments
Personalised Assessments
Assess
November 5, 2023

POLYNOMIALS | Study

Pre-Requisires

Test & Enrich

English Version

Speed Notes

Notes For Quick Recap

Study Tools

Audio, Visual & Digital Content

Revision Notes on Polynomials

Polynomial

A polynomial is an algebraic expression that includes constants, variables, and exponents. It is the expression in which the variables have only positive integral powers.

Example

1. 4x³ + 3x² + x +3 is a polynomial in variable x.

2. 4x² + 3x^-1 – 4 is not a polynomial as it has negative power.

3. 3x^3/2+ 2x – 3 is not a polynomial. Polynomials

Polynomials are denoted by p (x), q (x), etc.
In the above polynomials, 2x², 3y, and 2 are the terms of the polynomial.
2 and 3 are the coefficients of x² and y, respectively.
x and y are the variables.
2 is the constant term, which has no variable.

Polynomials in One Variable

If there is only one variable in the expression, then this is called the polynomial in one variable.

Example

x³ + x – 4 is polynomial in variable x and is denoted by p(x).
r² + 2 is polynomial in variable r and is denoted by p(r).

Types of polynomials on the basis of the number of terms

Types of polynomials on the basis of the number of degrees

The highest value of the power of the variable in the polynomial is the degree of the polynomial.

Zeros of a Polynomial

If p(x) is a polynomial, then the number ‘a’ will be the zero of the polynomial with p(a) = 0. We can find the zero of the polynomial by equating it to zero.

Example: 1

The given polynomial is p(x) = x – 4

To find the zero of the polynomial, we will equate it to zero.

x – 4 = 0

x = 4

p(4) = x – 4 = 4 – 4 = 0

This shows that if we place 4 in place of x, we get the value of the polynomial as zero. So 4 is the zero of this polynomial. And also, we are getting the value 4 by equating the polynomial with 0.

So 4 is the zero of the polynomial or the root of the polynomial.

The root of the polynomial is basically the x-intercept of the polynomial.

If the polynomial has one root, it will intersect the x-axis at one point only, and if it has two roots, it will intersect at two points, and so on.

Example: 2

Find p (1) for the polynomial p (t) = t² – t + 1

p (1) = (1)² – 1 + 1

= 1 – 1 + 1

= 1

Remainder Theorem

We know the property of division which follows in the basic division, i.e.

Dividend = (Divisor × Quotient) + Remainder

This follows the division of polynomials.

If p(x) and g(x) are two polynomials in which the degrees of p(x) ≥ degree of g(x) and g(x) ≠ 0 are given, then we can get the q(x) and r(x) so that:

P(x) = g(x) q(x) + r(x),

where r(x) = 0 or degree of r(x) < degree of g(x).

It says that p(x) divided by g(x), gives q(x) as a quotient and r(x) as a remainder.

Let’s understand it with an example

Division of a Polynomial with a Monomial

We can see that ‘x’ is common in the above polynomial, so we can write it as

Hence, 3x²+ x + 1 and x the factors of 3x³ + x² + x.

Steps of the Division of a Polynomial with a Non –Zero Polynomial

Divide x² – 3x -10 by 2 + x

Step 1: Write the dividend and divisor in descending order, i.e., in the standard form. x² – 3x -10 and x + 2

Divide the first term of the dividend with the first term of the divisor.

x²/x = x this will be the first term of the quotient.

Step 2: Now multiply the divisor by this term of the quotient and subtract it from the dividend.

Step 3: Now the remainder is our new dividend, so we will repeat the process again by dividing the dividend by the divisor.

Step 4: – (5x/x) = – 5

Step 5:

The remainder is zero.

Hence x² – 3x – 10 = (x + 2)(x – 5) + 0

Dividend = (Divisor × Quotient) + Remainder

The Remainder Theorem says that if p(x) is any polynomial of degree greater than or equal to one and let ‘t’ be any real number and p (x) is divided by the linear polynomial x – t, then the remainder is p(t).

As we know,

P(x) = g(x) q(x) + r(x)

If p(x) is divided by (x-t) then

If x = t

P (t) = (t – t). q (t) + r = 0

To find the remainder or to check the multiple of the polynomial, we can use the remainder theorem.

Example:

What is the remainder if a⁴ + a³ – 2a² + a + 1 is divided by a – 1.

Solution:

P(x) = a⁴ + a³ – 2a² + a + 1

To find the zero of (a – 1), we need to equate it to zero.

a -1 = 0

a = 1

p (1) = (1)⁴ + (1)³ – 2(1)² + (1) + 1

= 1 + 1 – 2 + 1 + 1

= 2

So by using the remainder theorem, we can easily find the remainder after the division of the polynomial.

Factor Theorem

The factor theorem says that if p(y) is a polynomial with degree n≥1 and t is a real number, then

(y – t) is a factor of p(y), if p(t) = 0, and
P (t) = 0 if (y – t) is a factor of p (y).

Example: 1

Check whether g(x) = x – 3 is the factor of p(x) = x³– 4x²+ x + 6 using the factor theorem.

Solution:

According to the factor theorem, if x – 3 is the factor of p(x), then p(3) = 0, as the root of x – 3 is 3.

P (3) = (3)³– 4(3)² + (3) + 6

= 27 – 36 + 3 + 6 = 0

Hence, g (x) is the factor of p (x).

Example: 2

Find the value of k, if x – 1 is a factor of p(x) = kx²– √2x + 1

Solution:

As x -1 is the factor, p(1) = 0

Factorization of Polynomials

Factorization can be done by three methods

1. By taking out the common factor

If we have to factorise x² –x then we can do it by taking x common.

x(x – 1) so that x and x-1 are the factors of x² – x.

2. By grouping

ab + bc + ax + cx = (ab + bc) + (ax + cx)

= b(a + c) + x(a + c)

= (a + c)(b + x)

3. By splitting the middle term

x² + bx + c = x² + (p + q) + pq

= (x + p)(x + q)

This shows that we have to split the middle term in such a way that the sum of the two terms is equal to ‘b’ and the product is equal to ‘c’.

Example: 1

Factorize 6x² + 17x + 5 by splitting the middle term.

Solution:

If we can find two numbers p and q such that p + q = 17 and pq = 6 × 5 = 30, then we can get the factors.

Some of the factors of 30 are 1 and 30, 2 and 15, 3 and 10, 5 and 6, out of which 2 and 15 is the pair which gives p + q = 17.

6x² + 17x + 5 =6 x² + (2 + 15) x + 5

= 6 x² + 2x + 15x + 5

= 2 x (3x + 1) + 5(3x + 1)

= (3x + 1) (2x + 5)

Algebraic Identities

1. (x + y)²= x²+ 2xy + y²

2. (x – y)² = x²– 2xy + y²

3. (x + y) (x – y) = x² – y²

4. (x + a) (x + b) = x² + (a + b)x + ab

5. (x + y + z)²= x²+ y²+ z²+ 2xy + 2yz + 2zx

6. (x + y)³ = x³ + y³ + 3xy(x + y) = x³+ y³ + 3x²y + 3xy²

7. (x – y)³ = x³– y³ – 3xy(x – y) = x³– y³ – 3x²y + 3xy²

8. x³+ y³ = (x + y)(x² – xy + y²)

9. x³ – y³= (x – y)(x² + xy + y²)

10. x³+ y³ + z³– 3xyz = (x + y + z)(x² + y²+ z² – xy – yz – zx) x³ + y³ + z³ = 3xyz if x + y + z = 0

Example: 2

Factorize 8x³ + 27y³ + 36x²y + 54xy²

Solution:

The given expression can be written as

= (2x)³+ (3y)³ + 3(4x²) (3y) + 3(2x) (9y²)

= (2x)³ + (3y)³ + 3(2x)²(3y) + 3(2x)(3y)²

= (2x + 3y)³ (Using Identity VI)

= (2x + 3y) (2x + 3y) (2x + 3y) are the factors.

Example: 3

Factorize 4x² + y² + z² – 4xy – 2yz + 4xz.

Solution:

4x² + y² + z² – 4xy – 2yz + 4xz = (2x)²+ (–y)² + (z)² + 2(2x) (-y)+ 2(–y)(z) + 2(2x)(z)

= [2x + (- y) + z]² (Using Identity V)

= (2x – y + z)² = (2x – y + z) (2x – y + z)

Hindi Version

Dig Deep

Topic Level Resources

Sub – Topics

Select A Topic

Topic:

Chapters Index

Select Another Chapter

Assessments

Personalised Assessments

CIRCLES | Study
Assess
Interact
Pre-Requisires
Test & Enrich
Pre – Requisite

English Version
Circles | Speed Notes
Notes For Quick Recap
Introduction to Circles
There are many objects in our life which are round in shape. A few examples are the clock, dart board, cartwheel, ring, Vehicle wheel, Coins, etc. (Scroll down to continue …)
Study Tools
Audio, Visual & Digital Content
Circles
Any closed shape with all points connected at equidistant from the centre forms a Circle.
Any point which is equidistant from anywhere from its boundary is known as the Centre of the Circle.
Radius is a Latin word which means ‘ray’ but in the circle it is the line segment from the centre of the circle to its edge. So any line starting or ending at the centre of the circle and joining anywhere on the border of the circle is known as the Radius of Circle.
Interior and Exterior of a Circle
In a flat surface, the interior of a circle is the line whose distance from the centre is less than the radius.
The exterior of a circle is the line in the plane whose distance from the centre is larger than the radius.
Terms related to circle
Chord: Any straight line segment that’s both endpoints falls on the boundary of the circle is known as Chord. In Latin, it means ‘bowstring’.
Diameter: Any straight line segment or Chord which passes through the centre of the Circle and its endpoints connects on the boundary of the Circle is known as the Diameter of Circle. So in a circle Diameter is the longest chord possible in a circle.
Arc: Any smooth curve joining two points is known as Arc. So in Circle, we can have two possible Arcs, the bigger one is known as Major Arc and the smaller one is known as Minor Arc.
Circumference: It is the length of the circle if we open and straighten it out to make a line segment.
Segment and Sector of the Circle
A segment of the circle is the region between either of its arcs and a chord. It could be a major or minor segment.
Sector of the circle is the area covered by an arc and two radii joining the centre of the circle. It could be the major or minor sector.
Angle Subtended by a Chord at a Point
If in a circle AB is the chord and is making ∠ACB at any point of the circle then this is the angle subtended by the chord AB at a point C.
Likewise, ∠AOB is the angle subtended by chord AB at point O i.e. at the centre and ∠ADB is also the angle subtended by AB at point D on the circle.
Theorem 1: Any two equal chords of a circle subtend equal angles at the centre.
Here in the circle, the two chords are given and PQ = RS with centre O.
So OP = OS = OQ = OR (all are radii of the circle)
∆POQ ≅ ∆SOR
∠POQ = ∠SOR
This shows that the angles subtended by equal chords to the centre are also equal.
Theorem 2: If the angles made by the chords of a circle at the centre are equal, then the chords must be equal.
This theorem is the reverse of the above Theorem 1.
Perpendicular from the Centre to a Chord
Theorem 3: If we draw a perpendicular from the centre of a circle to any chord then it bisects the chord.
If we draw a perpendicular from the centre to the chord of the circle then it will bisect the chord. And the bisector will make a 90° angle to the chord.
Theorem 4: The line which is drawn from the centre of a circle to bisect a chord must be perpendicular to the chord.
If we draw a line OB from the centre of the circle O to the midpoint of the chord AC i.e. B, then OB is the perpendicular to the chord AB.
If we join OA and OC, then
In ∆OBA and ∆OBC,
AB = BC (B is the midpoint of AC)
OA = OC (Both are the radii of the same circle)
OB = OB (same side)
Hence, ΔOBA ≅ ΔOBC (both are congruent by SSS congruence rule)
⇒ ∠OBA = ∠OBC (respective angles of congruent triangles)
∠OBA + ∠OBC = ∠ABC = 180° [Linear pair]
∠OBC + ∠OBC = 180° [Since ∠OBA = ∠OBC]
2 x ∠OBC = 180°
∠OBC = 90^o
∠OBC = ∠OBA = 90°
∴ OB ⊥ AC
Circle through Three Points
Theorem 5: There is one and only one circle passing through three given non-collinear points.
In this figure, we have three non-collinear points A, B and C. Let us join AB and BC and then make the perpendicular bisector of both so that RS and PQ the perpendicular bisector of AB and BC respectively meet each other at Point O.
Now take the O as centre and OA as the radius to draw the circle which passes through the three points A, B and C.
This circle is known as Circumcircle. Its centre and radius are known as the Circumcenter and Circumradius.
Equal Chords and Their Distances from the Centre
Theorem 6: Two equal chords of a circle are at equal distance from the centre.
AB and CD are the two equal chords in the circle. If we draw the perpendicular bisector of these chords then the line segment from the centre to the chord is the distance of the chord from the centre.
If the chords are of equal size then their distance from the centre will also be equal.
Theorem 7: Chords at equal distance from the centre of a circle are also equal in length. This is the reverse of the above theorem which says that if the distance between the centre and the chords are equal then they must be of equal length.
Angle Subtended by an Arc of a Circle
The angle made by two different equal arcs to the centre of the circle will also be equal.
There are two arcs in the circle AB and CD which are equal in length.
So ∠AOB = ∠COD.
Theorem 8: The angle subtended by an arc at the centre is twice the angle subtended by the same arc at some other point on the remaining part of the circle.
In the above figure ∠POQ = 2∠PRQ.
Theorem 9: Angles from a common chord which are on the same segment of a circle are always equal.
If there are two angles subtended from a chord to any point on the circle which are on the same segment of the circle then they will be equal.
∠a = (1/2) ∠c (By theorem 8)
∠b = (1/2) ∠c
∠a = ∠b
Cyclic Quadrilaterals
If all the vertices of the quadrilateral come in a circle then it is said to be a cyclic quadrilateral.
Theorem 10: Any pair of opposite angles of a cyclic quadrilateral has the sum of 180º.
∠A + ∠B + ∠C + ∠D = 360º (angle sum property of a quadrilateral)
∠A + ∠C = 180°
∠B + ∠D = 180º
Theorem 11: If the pair of opposite angles of a quadrilateral has a sum of 180º, then the quadrilateral will be cyclic.
This is the reverse of the above theorem.
Hindi Version
Dig Deep
Topic Level Resources
Sub – Topics
Select A Topic
Topic:
Chapters Index
Select Another Chapter
Assessments
Personalised Assessments
Assess
November 5, 2023
TRIANGLES | Study
Assess
Interact
Pre-Requisires
Test & Enrich
Pre – Requisite

English Version
Triangles | Speed Notes
Notes For Quick Recap
Similar Geometric Figures:
Two geometric figures which are the same in shape, such that one is simply a copy of the other on a smaller scale or a larger scale, are called similar geometric figures.
Two geometric figures are said to be similar if and only if they have the same shape but not necessarily the same size. Two congruent geometric figures are always similar but converse may or may not be true. (Scroll down to read more …)
Study Tools
Audio, Visual & Digital Content
Similar Polygons: Two polygons of the same number of sides are similar, if
(i) their corresponding angles are equal and
(ii) their corresponding sides are in proportion or their corresponding sides are in the same ratio.
The same ratio of the corresponding sides is referred to as the representative fraction or the scale factor for the polygons.
Similar Triangles :
Two triangles are said to be similar,
if (i) their corresponding angles are equal and
ii) their corresponding sides are in proportion (are in the same ratio).
Basic Proportionality Theorem (or Thales Theorem) : 1
If a line is drawn parallel to one side of a triangle intersecting the other two sides, then it divides the two sides in the same ratio. Or If a line is drawn parallel to one side of a triangle, intersecting the other two sides in distinct points, the other two sides are divided in the same ratio i .e.. If in ∆ABC, l∥ BC, intersecting in D and E. then
Converse of Basic Proportionality Theorem :
If a line divides any two sides of a triangle in the sameratio, the line is parallel to the third side i.e.
In ∆ABC, if l intersects AB in D and AC in E, such that:
Criteria for Similarity of Triangles:
Two triangles are said to be similar, if
(i) their corresponding angles are equal and (ii) their corresponding sides are in proportion (or are in the same ratio).
2 (i) AA or AAA Similarity Criterion : If two angles of one triangle are equal to two corresponding angles of another triangle, then the triangles are similar. If two angles of one triangle are respectively equal to the two angles of another triangle, then the third angles of the two triangles are necessarily equal, because the sum of three angles of a triangle is always 180 ⁰ .
(ii) SAS Similarity Criterion : If one angle of a triangle is equal to one angle of another triangle and the sides including these angles are in the same ratio, then the two triangles are similar. Or If two sides of a triangle are proportional to two corresponding sides of another triangle and the angles included between them are equal, then the triangles are similar.
iii) SSS Similarity Criterion : If in two triangles, sides of one triangle are proportional (or are in the same ratio) to the sides of the other triangle, then the triangles are similar. If ∆ABC~ ∆PQR by any one similarity criterion, then ∠A=∠P, ∠B=∠Q, ∠C=∠R and
i.e., A and P, B and Q, C and R are the corresponding vertices, also AB and PQ. BC and QR. CA and RP are the corresponding sides. 3 Areas of Similar Triangles: The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides. – The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding medians. – The ratio of the areas of two similar triangles is equal to the ratio of the squares of their corresponding altitudes. – The ratio of the areas of two similar triangles is equal to the ratio of the squares of their corresponding angle bisectors. Pythagoras Theorem : In a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides. Converse of Pythagoras Theorem : In a triangle, if the square of one side is equal to the sum of the squares of the other two sides, then the angle opposite the first side is a right angle. If a perpendicular is drawn from the vertex of the right angle of a right triangle to the hypotenuse, the triangles on each side of the perpendicular are similar to the whole triangle and similar to each other i .e ..
If in ∆ABC, ∠B=90^0 and BD ⊥ AC, then (i) ∆ADB ~ ∆ABC (ii) ∆BDC ~ ∆ABC (iii) ∆ADB ~ ∆BDC

Hindi Version
Dig Deep
Topic Level Resources
Sub – Topics
Select A Topic
Topic:
Chapters Index
Select Another Chapter
Assessments
Personalised Assessments
Assess
November 5, 2023
STATISTICS | Study
Assess
Interact
Pre-Requisires
Test & Enrich
Pre – Requisite

English Version
Speed Notes
Notes For Quick Recap
Study Tools
Audio, Visual & Digital Content
Statistics
Statistics is the study of collection, organization, analysis and interpretation of data.
Data
Data is a distinct piece of information in the form of fact or figures collected or represented for any specific purpose. The word data is derived from the Latin word Datum.
Collection of Data
In general, data is of two types. They are:
Primary Data
Secondary Data
Primary Data
Primary data is the data collected from any firsthand experience for an explicit use or purpose.
Secondary data
Secondary data is the data collected by any third party for a different purpose other than the user.
Presentation of Data
After collecting data it is important to present it meaningfully. There are many ways to present data.
1. Raw Data or Ungrouped Data
a. Raw Data or Ungrouped Data is the collected data without any change in its form.
Example
The marks obtained by 10 students in a Mathematics test are:
55 36 95 73 60 42 25 78 75 62
Range
Range is the difference between the highest and the lowest values of data.
For Above data: Range = 95 – 36 = 59
b. Frequency Distribution Table – Frequency Distribution Table is the data of a large number of items converted into tabular form.
Frequency is the number of times the item comes to the table.
2. Grouped Data
To present the very large number of items in the data we use a grouped distribution table.
Grouped Distribution Table
a. Class Interval – The group used to classify the data is called the class interval i.e. 20 – 30, 30 – 40.
b. Upper Limit – In each class interval, the greatest number is the upper-class limit.
c. Lower Limit – In each class interval, the smallest number is the lower class limit.
d. Class Size – It is the difference between the upper limit and the lower limit i.e. 10.
Class Size = Upper Limit – Lower Limit
e. Class Mark – The midpoint of each class interval is the class mark.
Grouped data could be of two types as below:-
Inclusive or discontinuous Frequency Distribution.
Exclusive or continuous Frequency Distribution
Inclusive or discontinuous Frequency Distribution – If the upper limit of a class is different from the lower limit of its next class then it is said to be an Inclusive or discontinuous Frequency Distribution.
Example
Draw the histogram of the following frequency distribution.
Daily earnings (in Rs) 700 – 749 750 – 799 800 – 849 850 – 899 900 – 949 950 – 999
No. of stores 6 9 2 7 11 5
Exclusive or continuous Frequency Distribution – If the upper limit of a class is the same as the lower limit of its next class then it is said to be exclusive or continuous Frequency Distribution
Example
Draw the histogram of the following frequency distribution.
Daily earnings (in Rs) 700 – 750 750 – 800 800 – 850 850 – 900 900 – 950 950 – 1000
No. of stores 6 9 2 7 11 5
Graphical Representation of Data
Since a picture represents better than a thousand words, The data is presented graphically. Some of the methods of representing the data graphically are:
1. Bar Graph
2. Histogram
3. Frequency Polygon
1. Bar Graph
It is the easiest way to represent the data in the form of rectangular bars so it is called Bar graph.
The thickness of each bar should be the same.
The space between the bars should also be the same.
The height of the bar should be according to the numerical data to be represented.
Example
Represent the average monthly rainfall of Nepal for the first six months in the year 2014.
Month Jan Feb Mar Apr May Jun
Average rainfall 45 65 40 60 75 30
Solution
On the x-axis mark the name of the months.
On the y-axis mark the class interval which we have chosen.
Then mark the average rainfall respective to the name of the month by the vertical bars.
The bars could be of any width but should be the same.
This is the required bar graph.
2. Histogram
It is similar to Bar graph, but it is used in case of a continuous class interval.
The class intervals are to be taken along an x-axis.
The height represents the frequencies of the respective class intervals.
Example
Draw the histogram of the following frequency distribution.
Daily earnings (in Rs) 700 – 750 750 – 800 800 – 850 850 – 900 900 – 950 950 – 1000
No. of stores 6 9 2 7 11 5
Solution:
Mark the daily earnings on the x-axis.
Mark the no. of stores on the y-axis.
As the scale is starting from 700 so we will mark the zigzag to show the break.
Mark the daily earnings through the vertical bars.
3. Frequency Polygon
Procedure to draw the frequency polygon
First, we need to draw a histogram.
Then join the midpoint of the top of the bars to a line segment and the figure so obtained is the required frequency polygon.
The midpoint of the first bar is to be joined with the midpoint of the imaginary interval of the x-axis
The midpoint of the last bar is to be joined with the midpoint of the next interval of the x-axis.
If we need to draw the frequency polygon without drawing the histogram then first we need to calculate the class mark of each interval and these points will make the frequency polygon.
Example
Draw the frequency polygon of a city in which the following weekly observations were made in a study on the cost of living index without histogram.
Step 1: First of all we need to calculate the class mark of each class interval.
Step 2: Take the suitable scale and represent the class marks on the x-axis.
Step 3: Take the suitable scale and represent the frequency distribution on the y-axis.
Step 4: To complete the frequency polygon we will join it with the x-axis before the first class and after the last interval.
Step 5: Now plot the respective points and join to make the frequency polygon.
Measures of Central Tendency
To make all the study of data useful, we need to use measures of central tendencies. Some of the tendencies are
1. Mean
2. Median
3. Mode
1. Mean (Average)
The mean is the average of the number of observations. It is calculated by dividing the sum of the values of the observations by the total number of observations.
It is represented by x bar or.
The meanof n values x1, x2, x3, …… xn is given by
Mean of Grouped Data (Without Class Interval)
If the data is organized in such a way that the frequency is given but there is no class interval then we can calculate the mean by
where, x1, x2, x3,…… xn are the observations
f1, f2, f3, …… fn are the respective frequencies of the given observations.
Example
Here, x1, x2, x3, x4, and x5 are 20, 40, 60, 80,100 respectively.
and f1 , f2 , f3 , f4, f5 are 40, 60, 30, 50, 20 respectively.
2. Median
The median is the middle value of the given number of the observation which divides into exactly two parts.
For median of ungrouped data, we arrange it in ascending order and then calculated as follows
If the number of the observations is odd then the median will be Term
As in the above figure the no. of observations is 7 i.e. odd, so the median will beterm.
= 4^th term.
The fourth term is 44.
If the number of observations is even then the median is the average of n/2 and (n/2) +1 term.
Example
Find the median of the following data.
6, 7, 10, 12, 13, 4, 8, 12
1. First, we need to arrange it in ascending order.
4, 6, 7,8,10,12,12,13
2. The no. of observation is 8. As the no. of observation is even the median is the average of n/2 and (n/2)+1.
3.
4. 4^th term is 8 and the 5^th term is 10.
5. So the median
3. Mode
The mode is the value of the observation which shows the number that occurs frequently in data i.e. the number of observations which has the maximum frequency is known as the Mode.
Example
Find the Mode of the following data:
15, 20, 22, 25, 30, 20,15, 20,12, 20
Solution
Here the number 20 appears the maximum number of times so
Mode = 20.
Remark: The empirical relation between the three measures of central tendency is: 3 Median = Mode + 2 Mean
Hindi Version
Dig Deep
Topic Level Resources
Sub – Topics
Select A Topic
Topic:
Chapters Index
Select Another Chapter
Assessments
Personalised Assessments
Assess
November 5, 2023

SURFACE AREAS AND VOLUMES | Study

Pre-Requisires

Test & Enrich

English Version

Surface Areas and Volumes | Speed Notes

Notes For Quick Recap

Plane figure

The figures which we can be drawn on a flat surface or that lie on a plane are called Plane Figure.

Example – Circle, Square, Rectangle etc.

Solid figures

The 3D shapes which occupy some space are called Solid Figures.

Example – Cube, Cuboid, Sphere etc. (Scroll down to continue …)

Study Tools

Audio, Visual & Digital Content

Volume

Space occupied by any solid shape is the capacity or volume of that figure. The unit of volume is a cubic unit.

Surface Area

The area of all the faces of the solid shape is its total surface area. The unit of surface area is a square unit.

Lateral or Curved Surface Area

The surface area of the solid shape after leaving the top and bottom face of the figure is called the lateral surface of the shape. The unit of lateral surface area is a square unit.

Surface Area and Volume of a Cube

Cube is a solid shape having 6 equal square faces.

Lateral surface area of a cube	4s²
Total surface area of a cube	6s²
The volume of a cube	s³
Diagonal	√3 s, s = edge of the cube = side length of face of cube

Surface Area and Volume of a Cube

Example

What is the capacity of a cubical vessel having each side of 8 cm?

Solution

Given side = 8 cm So, Volume of the cubical vessel = l³ = (8)³ = 256 cm³.

Surface Area and volume of a Cuboid

Cuboid is a solid shape having 6 rectangular faces at a right angle.

Lateral surface area of a cuboid	2h(l + b)
Total surface area of a cuboid	2(lb + bh + lh)
Volume of a cuboid	lbh
Diagonal	l = length, b = breadth, h = height

Surface Area and volume of a Cuboid

Example

What is the surface area of a cereal box whose length, breadth and height is 20 cm, 8 cm and 30 cm respectively?

Solution

Given, length = 20 cm, breadth = 8 cm, Height = 30 cm

Total surface area of the cereal box = 2(lb + bh + lh)

= 2(20 × 8 + 8 × 30 + 20 × 30)

= 2(160 + 240 + 600)

= 2(1000) = 2000 cm².

Surface Area and Volume of a Right Circular Cylinder

If we fold a rectangular sheet with one side as its axis then it forms a cylinder. It is the curved surface of the cylinder. And if this curved surface is covered by two parallel circular bases then it forms a right circular cylinder.

Curved surface area of a Right circular cylinder	2πrh
Total surface area of a Right circular cylinder	2πr² + 2πrh = 2πr(r + h)
The volume of a Right circular cylinder	πr²h
	r = radius, h = height

Surface Area and Volume of a Right Circular Cylinder

Surface Area and Volume of a Hollow Right Circular Cylinder

If a right circular cylinder is hollow from inside then it has different curved surface and volume.

Curved surface area of a Right circular cylinder	2πh (R + r)
Total surface area of a Right circular cylinder	2πh (R + r) + 2π(R² – r²)
	R = outer radius, r = inner radius, h = height

Surface Area and Volume of a Hollow Right Circular Cylinder

Example

Find the Total surface area of a hollow cylinder whose length is 22 cm and the external radius is 7 cm with 1 cm thickness. (π = 22/7)

Solution

Given, h = 22 cm, R = 7 cm, r = 6 cm (thickness of the wall is 1 cm).

Total surface area of a hollow cylinder = 2πh(R + r) + 2π(R²– r²)

= 2(π) (22) (7+6) + 2(π)(7²– 6²)

= 572 π + 26 π = 598 π

= 1878.67 cm²

Surface Area and Volume of a Right Circular Cone

If we revolve a right-angled triangle about one of its sides by taking other as its axis then the solid shape formed is known as a Right Circular Cone.

Curved surface area of a Right Circular Cone	πrl = πr[√(h2 + r2)]
Total surface area of a Right Circular Cone	πr²+ πrl = πr(r + l)
The volume of Right Circular Cone	(1/3) πr²h
	r = radius, h = height, l = slant height

Surface Area and Volume of a Right Circular Cone

Surface Area and Volume of a Sphere

A sphere is a solid shape which is completely round like a ball. It has the same curved and total surface area.

Curved or Lateral surface area of a Sphere	4πr²
Total surface area of a Sphere	4πr²
Volume of a Sphere	(4/3) πr³
	R = radius

Surface Area and Volume of a Sphere

Surface Area and Volume of a Hemisphere

If we cut the sphere in two parts then is said to be a hemisphere.

Curved or Lateral surface area of a Sphere	2πr²
Total surface area of a Sphere	3πr²
Volume of a Sphere	(2/3) πr³
	r = radius

Surface Area and Volume of a Hemisphere

Example

If we have a metal piece of cone shape with volume 523.33 cm³ and we mould it in a sphere then what will be the surface area of that sphere?

Solution

Given, volume of cone = 523.33 cm³

Volume of cone = Volume of Sphere

Volume of sphere = 100 π cm³

125 = r³

r = 5

Surface area of a sphere = 4πr²

= 314.28 cm².

Hindi Version

Dig Deep

Topic Level Resources

Sub – Topics

Select A Topic

Topic:

Chapters Index

Select Another Chapter

Assessments

Personalised Assessments