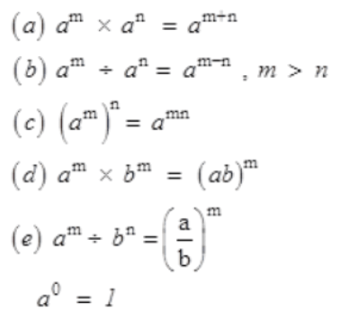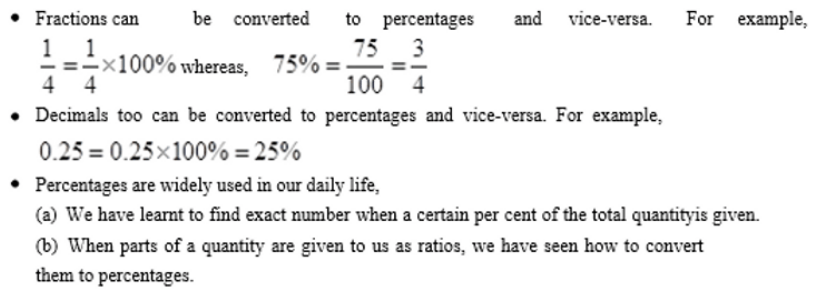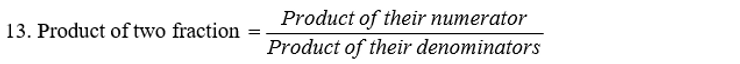RATIO AND PROPORTION | Study
Assess
Interact
Pre-Requisires
Test & Enrich
Pre – Requisite

English Version
Ratio and Proportion Comparison By Taking Difference | Speed Notes
Notes For Quick Recap
CHAPTER 12 Ratio and Proportion Comparison by taking difference: For comparing quantities of thesame type, wecommonly use themethod of taking difference between thequantities. Some times thecomparison by difference does not makebetter sense thanthe comparison by division. (Scroll down to continue)
Study Tools
Audio, Visual & Digital Content
Comparison by Division: In many situations, a more meaningful comparison between quantities is made byusing division, i.e.. by seeing how many times one quantity is to the other quantity. This method is known ascomparison by ratio. The comparison of two numbers or quantities bydivision is knownas the ratio. Symbol ‘:’is used todenote ratio. For comparison by ratio, thetwo quantities mustbe in thesame unit. Ifthey are not,they should beexpressed in thesame unit before the ratio istaken. For example, Isha’s weight is25 kg andher father’s weight is 75 kg.We say thatIsha’s father’s weight and Isha’s weight are in theratio 3 : 1

Hindi Version
Dig Deep
Topic Level Resources
Sub – Topics
Select A Topic
Topic:
Chapters Index
Select Another Chapter
Assessments
Personalised Assessments
Assess
November 5, 2023
CBSE 6 | Mathematics – Study – Free
Educational Tools | Full Course
Study Tools
Audio, Visual & Digital Content
Assessment Tools
Assign, Assess & Analyse
Connnect With Us
Enrich our growing community
[ultimatemember form_id=”26482″]
November 5, 2023
KNOWING OUR NUMBERS | Study
Assess
Interact
Pre-Requisires
Test & Enrich
Pre – Requisite

English Version
Whole Numbers | Speed Notes
Notes For Quick Recap
Whole Numbers The numbers 1,2, 3, ……which we use for counting are known as natural numbers. If you add 1 to a natural number, we get its successor. If you subtract 1 from a natural number, you get its predecessor. (Scroll down to continue …)
Study Tools
Audio, Visual & Digital Content
Every natural number has a successor. Every natural number except 1 has a predecessor.
Whole Numbers
Whole numbers are formed by adding zero to the collection of natural numbers. Hence, the set of whole numbers includes 0, 1, 2, 3, and so on.
Key Properties of Whole Numbers:
Successors and Predecessors:
Every whole number has a successor. For example:
The successor of 0 is 1.
The successor of 1 is 2.
The successor of 2 is 3.
Every whole number except zero has a predecessor. For example:
The predecessor of 1 is 0.
The predecessor of 2 is 1.
The predecessor of 3 is 2.
Relationship with Natural Numbers:
All natural numbers (1, 2, 3, …) are whole numbers, but not all whole numbers are natural numbers since whole numbers include 0.
Number Line Representation:
Whole Number Line
To visualize whole numbers, we can draw a number line starting from 0:
Mark points at equal intervals to the right: 0, 1, 2, 3, …
This number line allows us to carry out operations:
Addition: Moving to the right (e.g., 1 + 2 = 3).
Subtraction: Moving to the left (e.g., 3 – 1 = 2).
Multiplication: Making equal jumps (e.g., 2 × 3 means jumping twice the distance of 2, reaching 6).
Division: Although division can be tricky, it involves partitioning. For example, 6 ÷ 2 means splitting 6 into 2 equal parts, resulting in 3.
Closure Properties:
Adding two whole numbers always results in a whole number:
Examples:
2 + 3 = 5
0 + 4 = 4
1 + 1 = 2
Multiplying two whole numbers also results in a whole number:
Examples:
2 × 3 = 6
0 × 5 = 0
1 × 4 = 4
Whole numbers are closed under subtraction only if the result is non-negative:
Examples:
2 – 1 = 1
5 – 3 = 2
3 – 3 = 0
Yet, if the result is negative, they are not closed under subtraction:
Example: 2 – 3 = -1 (not a whole number).
So, the whole numbers are not not closed under subtraction.
Division by whole numbers is defined only when the divisor is not zero, and the result is a whole number:
Examples:
6 ÷ 2 = 3
8 ÷ 4 = 2
0 ÷ 5 = 0
Division by zero is undefined (e.g., 5 ÷ 0).
So, the whole numbers are not not closed under division.
Identity Elements:
Zero acts as the identity for addition:
Example: 5 + 0 = 5.
The whole number 1 acts as the identity for multiplication:
Example: 3 × 1 = 3.
Commutative and Associative Properties:
Addition is commutative:
Examples:
2 + 3 = 3 + 2
1 + 4 = 4 + 1
0 + 5 = 5 + 0
Multiplication is also commutative:
Examples:
2 × 3 = 3 × 2
1 × 4 = 4 × 1
0 × 5 = 5 × 0
Both addition and multiplication are associative:
Examples for addition:
(1 + 2) + 3 = 1 + (2 + 3)
(0 + 4) + 1 = 0 + (4 + 1)
(2 + 2) + 2 = 2 + (2 + 2)
Examples for multiplication:
(1 × 2) × 3 = 1 × (2 × 3)
(0 × 4) × 1 = 0 × (4 × 1)
(2 × 2) × 2 = 2 × (2 × 2)
Distributive Property:
Multiplication distributes over addition:
Example: 2 × (3 + 4) = 2 × 3 + 2 × 4.
Understanding these properties helps simplify calculations. It enhances our grasp of numerical patterns. These patterns are not only interesting but also practical for mental math.
Hindi Version
Dig Deep
Topic Level Resources
Sub – Topics
Select A Topic
Topic:
Chapters Index
Select Another Chapter
Assessments
Personalised Assessments
Assess
November 5, 2023
PLAYING WITH NUMBERS | Study
Assess
Interact
Pre-Requisires
Test & Enrich
Pre – Requisite

English Version
PLAYING WITH NUMBERS | Speed Notes
Notes For Quick Recap
We have discussed multiples, divisors, factors and have seenhow to identify factors and multiples. We have discussed and discovered thefollowing: (a) A factor of a number is an exactdivisor of thatnumber. (Scroll down to continue …)
Study Tools
Audio, Visual & Digital Content
(b) Every number is a factor of itself. 1 is a factor ofevery number.
(c) Every factor ofa number isless than or equal tothe given number.
(d) Every number isa multiple ofeach of itsfactors.
(e) Every multiple ofa given number is greater thanor equal tothat number.
(f) Every number is a multiple of itself.
We have learnt that – (a) The number otherthan 1, withonly factors namely 1 and thenumber itself, isa prime number. Numbers that have more than two factors are called composite numbers. Number 1is neither prime nor composite.
(b) The number 2is the smallest prime number andis even. Every prime number other than 2 isodd.
(c) Two numbers withonly 1 asa common factor are called co-prime numbers.
(d) If a number is divisible byanother number thenit is divisible by each of the factors of that number.
(e) A number divisible by two co-prime numbers is divisible by their product also.
We have discussed how we can find just by looking at a number, whether it is divisible by small numbers 2,3,4,5,8,9 and 11.
We have explored the relationship between digits of thenumbers and theirdivisibility by different numbers.
(a) Divisibility by 2,5and 10 canbe seen byjust the lastdigit.
(b) Divisibility by 3and 9 ischecked by finding the sum ofall digits.
(c) Divisibility by 4 and 8is checked bythe last 2and 3 digits respectively.
(d) Divisibility of11 is checked by comparing thesum of digits at odd andeven places.
We have discovered that if twonumbers are divisible by a number then their sum and difference are also divisible by that number.
We have learnt that – (a) The Highest Common Factor (HCF) of two ormore given numbers is the highest of their common factors.
(b) The Lowest Common Multiple (LCM) of two ormore given numbers is the lowest of their common multiples.

Hindi Version
Dig Deep
Topic Level Resources
Sub – Topics
Select A Topic
Topic:
Chapters Index
Select Another Chapter
Assessments
Personalised Assessments
Assess
November 5, 2023
BASIC GEOMETRICAL IDEAS | Study
Assess
Interact
Pre-Requisires
Test & Enrich
Pre – Requisite

English Version
Basic Geometrical Ideas | Speed Notes
Notes For Quick Recap
Geometry
Geometry is a branch of mathematics concerned with properties of space such as the distance, shape, size, and relative position of figures. A mathematician who works in the field of geometry is called a 🎉geometer. (Scroll down to continue …)
Study Tools
Audio, Visual & Digital Content
Basic Geometrical Ideas | Speed Notes
Notes For Quick Recap
Geometry
Geometry is a branch of mathematics concerned with properties of space such as the distance, shape, size, and relative position of figures. A mathematician who works in the field of geometry is called a 🎉geometer.
Space
Space: space refers to a set of points that form a particular type of structure.
Plane
A plane is a flat surface that extends infinitely in all directions
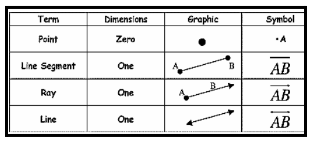
Point
Point is an exact position or location in space with no dimensions.
Mathematically, a point is defined as a circle with zero radius.
Since it is not possible its is represented by a very small dot.
A point is usually represented by a capital letter.
In mathematical terms, pont is a cirlce with no radius. It does mean that a very very small circle.
A point determines a location. It is usually denoted by a capital letter.
Lines And Its Types
Ray
A Ray is a straight path that stars at a point and extends infinitely in one direction.
Note: A ray is a portion of line starting at a point and extends in one direction endlessly. A ray has only one endpoint (Initial point).
Line or Straight Line
A line is a straight path that extends infinitely in two opposite directions. It can be treated as a combination of two rays starting from the same point but extending in the opposite directions.
Note: A line has no end points.
Line Segment:
A line segment is the part of a line between two points. (Segment means part).
The length of a line segment is the shortest length between two end points.
The line segment has two end points. Note: A line Segment has two endpoints. (both Initial and end points). (Scroll down to continue …).
Intersecting Lines and Non-intersecting Lines
Intersecting And Parallel Lines
Parallel Lines
The lines which never cross each other at any point are called Parallel lines or Non-intersecting lines.
In other words, lines that are always the same distance apart from each other and that never meet are called Parallel lines Or Non-intersecting lines.
The perpendicular length between two lines is the distance between parallel lines.
Note: Parallel lines do not have any common point.
Intersecting Lines
The lines which cross (meet) each other at a point are called Intersecting Lines or non-parallel lines.
Intersecting lines meet at only one point.
Angle
An angle is made up of two rays starting from a common end point.
An angle leads to three divisions of a region:
On the angle, the interior of the angle and the exterior of the angle.
Curve
In geometry, a curve is a line or shape that is drawn smoothly and continuously in a plane with bends or turns.
In other words, Curve is a drawing (straight or non-straight) made without lifting the pencil may be called a curve.
Mathematicians define a curve as any shape that can be drawn without lifting the pen.
In Mathematics, A curve is a continuous and smooth line that is defined by a mathematical function or parametric equations.
Note: In this sense, a line is also a curve.
Types of Curves
Simple Or Open And Closed Curves
Cureves are two types based on intersection (crossing). They are (i) Simple or Open curve (ii) Closed curve.
Simple Curve
Simple or open curve is a curve that does not cross (intersect) itself.
Closed Curve
Closed curve is a curve that crosses (intersects) itself.
Concave And Convex Curves
Curves are of two types. They are concave curve and convex curve.
Concave Curve:
A curve is concave is a curve that curves inward, resembling a cave.
Examples:
   – The interior of a circle.
   – The graph of a concave function like y = -x².
Convex Curves:
A curve is convex if it curves outward.
Examples:
   – The exterior of a circle.
   – The graph of a convex function like y = x².
Polygon
A polygon is a simple closed figure formed by the line segments.
Types of Polygons
Polygons are classified into two types on the basis of interior angles: as (i) Convex polygon (ii) Concave polygon.
(a) Concave Polygon:
A concave polygon is a simple polygon that has at least one interior angle, that is greater than 180⁰ and less than 360⁰(Reflex angle).
And at Least one diagonal lies outside of the closed figure.
Atlest one diagonal lies outside of the polygon.
b. Convex Polygon:
A convex polygon is a simple polygon that has at least no interior angle that is greater than 180⁰ and less than 360⁰(Reflex angle).
And no diagonal lies outside of the closed figure.
In this case, the angles are either acute or obtuse (angle < 180 ^o).
Regular And Irregular Polygon
On the basis of sides, there are two types of polygons as Regular Polygon and Irregular Polygon
(a) Regular Polygon:
A convex polygon is called a regular polygon, if all its sides and angles are equal as shown in the following figures.
Each angle of a regular polygon of n-sides =
Part of Polygon
(i) Sides Of The Polygon
The line segments of a polygone are called sides of the polygon.
(ii) Adjacent Sides Of Polygon
Adjacent sides of a polygon are thesides of a polygon with a common end point.
(iii) Vertex Of Polygon
Vertext of a polygon is a point at which a pair of sides meet.
(iv) Adjacent Vertices
Adjacent vertices of polygon are the end points of the same side of the polygon.
(v) diagonal
Diagonal of a polygone is a line segment that joins the non-adjacent vertices of the polygon.
Triangle
A triangle is a three-sided polygon.
In other terms triangle is a three sided closed figure.
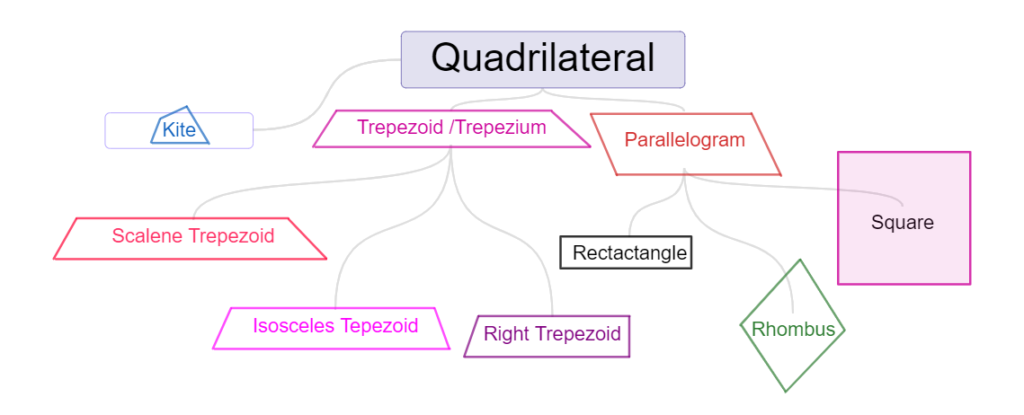
Quadrilateral
A quadrilateral is a four-sided polygon. (It shouldbe named cyclically).
In any
similar relations exist for the other three angles.
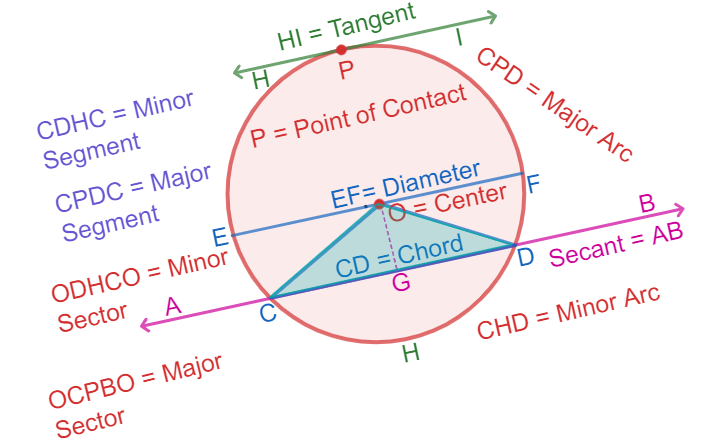
Circle And Its Parts
A circle is the path of a point moving at the same distance from a fixed point.
Centre Of Circle
Centre Of Circle is a point that is equidistant from any point on the boundary of the circle.
In other words the centre of the circles is a centre point of the circle.
Radius Of Circle
Radius of circle is the distance between the centre of the circle and any point on the boundary of the circle.
Circumference Of Circle
Circumference of circle is the length of the boundary of the circle.
Chord Of Circle
A chord of a circle is a line segment joining any two points on the circle.
A diameter is a chord passing throughthe Centre of the circle.
Sector Of Circle
A sector is the region in the interior of a circle enclosed by an arc on one side and a pair of radii on the other two sides.
Segment Of Circle
A segment of a circle is a region in the interior of the circle enclosed by an arc and a chord.
The diameter of a circle divides it into two semi-circles.
The diameter of a circle divides it into two semi-circles.

Hindi Version
Dig Deep
Topic Level Resources
Sub – Topics
Select A Topic
Topic:
Chapters Index
Select Another Chapter
Assessments
Personalised Assessments
Assess
November 5, 2023
UNDERSTANDING ELEMENTARY SHAPES | Study
Assess
Interact
Pre-Requisires
Test & Enrich
Pre – Requisite

English Version
Understanding Elementary Shapes |Speed Notes
Notes For Quick Recap
The distance betweenthe end pointsof a line segment is its length. A graduatedruler and the divider are useful to compare lengthsof line segments. When a hand of a clock moves from one position to another position we have an examplefor an angle. (Scroll down to continue …)
Study Tools
Audio, Visual & Digital Content
One full turn of the hand is 1 revolution.
A right angle is ¼ revolution and a straight angle is ½ a revolution. We use a protractor to measure the size of an angle in degrees.
The measure of a right angle is 90° and hence that of a straight angle is 180°.
An angle is acute if its measure is smaller than that of a right angle and is obtuseif its measure is greaterthan that of a right angle and less than a straightangle.
A reflex angle is largerthan a straight angle.
Two intersecting lines are perpendicular if the anglebetween them is 90°.
The perpendicular bisector of a line segmentis a perpendicular to the line segmentthat divides it into two equal parts.
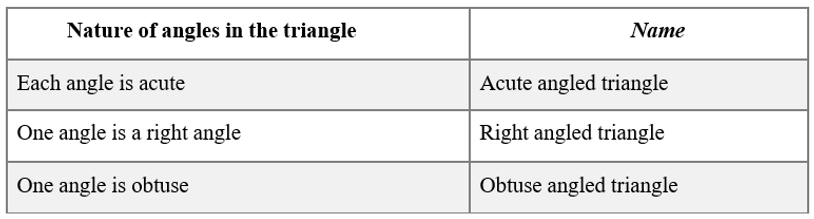
Triangles can be classified as follows based on their angles:
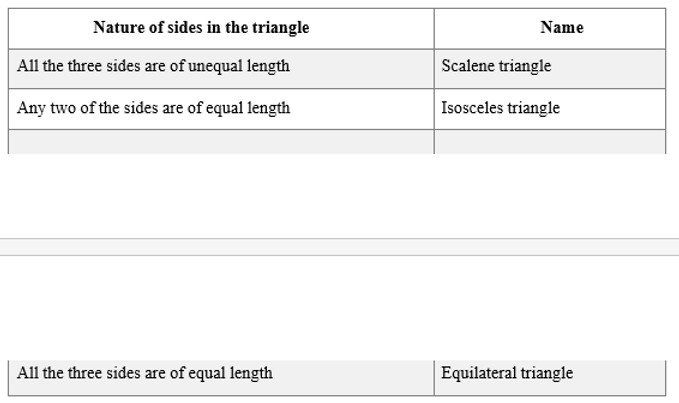
Triangles can be classified as follows based on the lengths of their sides:
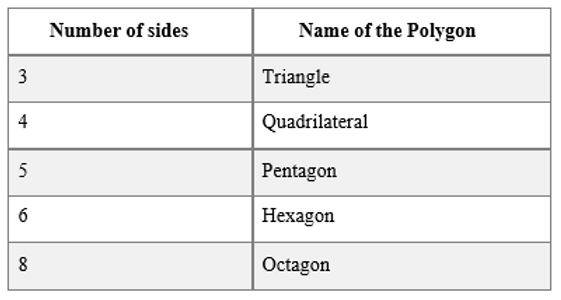
Polygons are namedbased on theirsides.
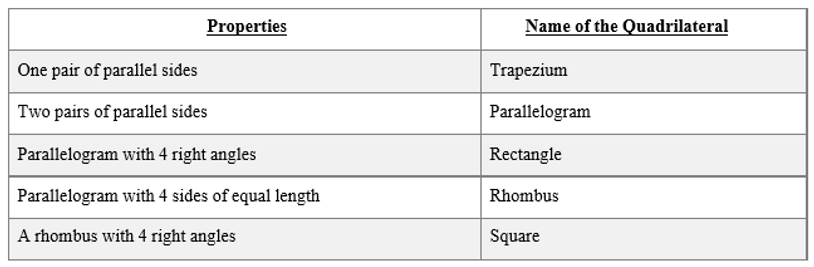
Quadrilaterals are furtherclassified with reference to their properties.
·We see aroundus many three dimensional shapes.Cubes, cuboids, spheres,
cylinders, cones,prisms and pyramidsare some of them.

Hindi Version
Dig Deep
Topic Level Resources
Sub – Topics
Select A Topic
Topic:
Chapters Index
Select Another Chapter
Assessments
Personalised Assessments
Assess
November 5, 2023
Visualising Solid Shapes | Study
Assess
Interact
Pre-Requisires
Test & Enrich
Pre – Requisite

English Version
Visualising SolidShapes | Speed Notes
Notes For Quick Recap
The circle, thesquare, the rectangle, the quadrilateral and the triangle are examples of plane figures; the cube, the cuboid, the sphere, the cylinder, the cone and the pyramid areexamples of solid shapes. (Scroll down to continue …)
Study Tools
Audio, Visual & Digital Content
Plane figures areof two-dimensions (2-D) and the solid shapes are of three- dimensions (3-D). The corners of a solid shape are called its vertices; theline segments ofits skeleton areits edges; and itsflat surfaces areits faces. A net is a skeleton-outline of a solid that can be folded to make it. The same solid can haveseveral types ofnets. Solid shapes can be drawn on a flat surface (like paper) realistically. We call this 2-D representation of a 3-Dsolid. Two types ofsketches of asolid are possible: (a) An oblique sketch does nothave proportional lengths. Still it conveys all important aspects of the appearance of the solid. (b) An isometric sketch is drawn on an isometric dot paper, a sample of which isgiven at theend of thisbook. In an isometric sketch of the solidthe measurements kept proportional. Visualising solidshapesis a veryuseful skill. Youshould be ableto see ‘hidden’ parts of thesolid shape. Different sections of a solid can be viewed in many ways: (a) One way is to viewby cutting or slicing the shape, whichwould result in the cross- section of thesolid. (b) Another way isby observing a 2-D shadow of a 3-Dshape. (c) A third wayis to lookat the shapefrom different angles; the front-view, theside- view and thetop view canprovide a lotof information aboutthe shape observed.
19. When a grouping symbol preceded by ‘ sign is removed or inserted, thenthe sign of eachterm of thecorresponding expression ischanged (from ‘ + ‘ to ‘−’ and from‘− ‘ to + ‘).

Hindi Version
Dig Deep
Topic Level Resources
Sub – Topics
Select A Topic
Topic:
Chapters Index
Select Another Chapter
Assessments
Personalised Assessments
Assess
November 5, 2023
Symmetry | Study
Assess
Interact
Pre-Requisires
Test & Enrich
Pre – Requisite

English Version
Congruence of Triangles | Speed Notes
Notes For Quick Recap
Congruence: The relation of two objects being congruent is called congruence. (Scroll down to continue …)
Study Tools
Audio, Visual & Digital Content
Chapter – 7
Congruence of Triangles
SSS Congruence of two triangles: Under a given correspondence, two triangles are congruent if the three sides of the one are equal to the three corresponding sides of the other.
SAS Congruenceof two triangles: Under a given correspondence, two triangles are
congruent if two sides and the angleincluded between them in one of the triangles are equal to the corresponding sides and the angle included between them of the other triangle.
ASA Congruence of two triangles: Under a given correspondence, two triangles are congruent if two anglesand the side included betweenthem in one of the triangles are equal to the corresponding angles and the side included between them of the other triangle.
RHS Congruence of two right-angled triangles: Under a given correspondence, two right-angled triangles are congruent if the hypotenuse and a leg of one of the triangles are equal to the hypotenuse and the corresponding leg of the other triangle.
There is no such thing as AAA Congruence of two triangles: Two triangles with equal corresponding angles need not be congruent. In such a correspondence, one of them can be an enlarged copy of the other.
(They would be congruent only if they are exact copies of one another).

Hindi Version
Dig Deep
Topic Level Resources
Sub – Topics
Select A Topic
Topic:
Chapters Index
Select Another Chapter
Assessments
Personalised Assessments
Assess
November 5, 2023
Rational Numbers | Study
Assess
Interact
Pre-Requisires
Test & Enrich
Pre – Requisite

English Version
Rational Numbers | Speed Notes
Notes For Quick Recap
Rational Number: A number that can be expressed in the form (Scroll down to continue …)
Audio, Visual & Digital Content
14. Every positive rational number is greater than zero.
15. Every negative rational number is less than zero.
16. The rational numbers can be represented on the number line.
Study Tools

Hindi Version
Dig Deep
Topic Level Resources
Sub – Topics
Select A Topic
Topic:
Chapters Index
Select Another Chapter
Assessments
Personalised Assessments
Assess
November 5, 2023
Perimeter and Area | Study
Assess
Interact
Pre-Requisires
Test & Enrich
Pre – Requisite

English Version
Perimeter and Area | Speed Notes
Notes For Quick Recap
Perimeter is the distance around a closed figure whereasarea is the part of plane occupied by the closedfigure.
Area is the measure of the part of plane or regionenclosed by it. (Scroll down to continue …)
Study Tools
Audio, Visual & Digital Content
We have learnt how to find perimeter and area of a squareand rectangle earlierclass.
They are:
(a) Perimeter of a square = 4 × side
(b) Perimeter of a rectangle = 2 × (length + breadth)
(c) Area of a square = side × side
(d) Area of a rectangle = length × breadth Areaof a parallelogram = base × height

Hindi Version
Dig Deep
Topic Level Resources
Sub – Topics
Select A Topic
Topic:
Chapters Index
Select Another Chapter
Assessments
Personalised Assessments
Assess
November 5, 2023
Exponents and Powers | Study
Assess
Interact
Pre-Requisires
Test & Enrich
Pre – Requisite

English Version
Exponents and Powers Exponents | Speed Notes
Notes For Quick Recap
Exponents are used to express large numbers in shorter form to make them easy to read, understand, compare and operate upon. (Scroll down to continue …)
Study Tools
Audio, Visual & Digital Content
Expressing Large Numbers in the Standard Form: Any number can be expressed as a decimal number between 1.0 and 10.0 (including 1.0) multiplied by a power of 10. Such form of a number is called its standard form or scientific motion. Very large numbers are difficult to read, understand, compare and operate upon. To make all these easier, we use exponents, converting many of the large numbers in a shorter form. The following are exponential forms of some numbers?
Here, 10, 3 and 2 are the bases, whereas 4, 5 and 7 are their respective exponents. We also say, 10,000 is the 4th power of 10, 243 is the 5th power of 3, etc. Numbers in exponential form obey certain laws, which are: For any non-zero integers a and b and whole numbers m and n,
(g) (–1) even number = 1 (–1) odd number = – 1

Hindi Version
Dig Deep
Topic Level Resources
Sub – Topics
Select A Topic
Topic:
Chapters Index
Select Another Chapter
Assessments
Personalised Assessments
Assess
November 5, 2023
The Triangle And Its Properties | Study
Assess
Interact
Pre-Requisires
Test & Enrich
Basics Of Geometry

English Version
Speed Notes
Notes For Quick Recap
Triangle
A closed plane figure bounded by three linesegments. The six elements of a triangle are its three angles and thethree sides. The line segment joining a vertex of a triangle to the mid point of its opposite side is called a medianof the triangle. (Scroll down to continue …)
Study Tools
Audio, Visual & Digital Content
Notes For Quick Recap
A closed plane figure bounded by three linesegments. The six elements of a triangle are its three angles and thethree sides. The line segment joining a vertex of a triangle to the mid point of its opposite side is called a medianof the triangle. (Scroll down to continue …)
Triangle:
A closed plane figure bounded by three line segments is called Triangle.
The six elements of a triangle are its three angles and the three sides. The line segment joining a vertex of a triangle to the midpoint of its
Median:
The opposite side is called the median of the triangle.
A triangle has three medians.
Altitude of the triangle:
The perpendicular line segment from vertex of a triangle to its opposite sides is called an altitude of the triangle.
A triangle has3 altitudes.
Type of triangle based onSides: Equilateral:
A triangle is said to be equilateral, if each one of its sides has the same length. In An equilateral triangle, each angle measures 60°.
Isosceles Triangle:
A triangle is said to be isosceles, if atleast any two of its sides are of same length. The non-equal side of an isosceles triangle is called its base; the base angles of an isosceles triangle have equal measure.
Scalene Triangle:
A triangle having all sides of different lengths. It has no two angles equal.
Property of the lengths of sides of a triangle:
The sum of the lengths of any two sides of a triangle is greater than the length of the third side. The difference between the lengths of any two sides is smaller than the length of the third side. This property is useful to know if it is possible to draw a triangle when the lengths of the three sides are known.
Types of Triangle based on Angles:
(i) Right Angled Triangle:
A triangle one of whose angles measures
(ii) Obtuse Angled Triangle:
A triangle one of whose angles measures more than
(iii) Acute Angled Triangle:
A triangle each of whose angles measures less than In a right angled triangle, the side opposite to the right angle is called the hypotenuse and the other two sides are called its legs.
Pythagoras property:
In a right-angled triangle, the square on the hypotenuse = the sum of the squares on its legs.If a triangle is not right-angled, this property does not hold good. Thisproperty is useful to decide whether a given triangle is right-angled
or not.
Exterior angle of a triangle:
An exterior angle of a triangle is formed, when a side of a triangle is produced. At each vertex, you have two ways of forming an exterior angle.
A property of exterior angles:
The measure of any exterior angle of a triangle is equal to the sum of the measures of its interior opposite angles.
The angle sum property of a triangle:
The total measure of the three angles of a triangle is 180°.
Property of the Lengths of Sides of a Triangle:
The sum of the lengths of any two sides of a triangle is always greater than the length of the third side. The difference of the lengths of any two sides of a triangle is always smaller than the length of the third side.
Important Formulas – TheTriangles and its Properties
1. A triangle is a figure made up by three line segments joining, in pairs, three non-collinear points. That is, if A, B, C are three non-collinear points, the figure formed by three line segments AB,BC and CA is called a triangle with vertices A, B, C.
2. The three line segments forming a triangle are called the sides of the triangle.
3. The three sides and three angles of a triangle are together called the six parts or elements of the triangle.
4. A triangle whose two sides are equal, is called an isosceles triangle.
5. A triangle whose all sides are equal, is called an equilateral triangle.
6. A triangle whose no two sides are equal, is called a scalene triangle.
7. A triangle whose all the angles are acute is called an acute triangle.
8. A triangle whose one of the angles is a right angle is called a right triangle.
9. A triangle whose one of the angles is an obtuse angle is called an obtuse triangle.
10. The interior of a triangle is made up of all such points P of the plane, as are enclosed by the triangle.
11. The exterior of a triangle is that part of the plane which consists of those points Q, which are neither on the triangle nor in its interior.
12. The interior of a triangle together with the triangle itself is called the triangular region.
13. The sum of the angles of a triangle is two right angles or 180°.
14. If a side of a triangle is produced, the exterior angle so formed is equal to the sum of the interior opposite angles.
15. In any triangle, an exterior angle is greater than either of the interior opposite angles.
16. The sum of any two sides of a triangle is greater than the third side.
17. In a right triangle, if a, b are the lengths of the sides and c that of the hypotenuse, then
18. If the sides of a triangle are of lengths a, b and c such that
then the triangle is right-angled and the side of length c is the hypotenuse.
19. Three positive numbers a, b, c in this order are said to form a Pythagorean triplet, if
Triplets (3, 4, 5) (5, 12,13), (8, 15, 17), (7,24, 25) and (12, 35,37) are somePythagorean triples.

Hindi Version
Dig Deep
Topic Level Resources
Sub – Topics
Select A Topic
Topic:
Chapters Index
Select Another Chapter
Assessments
Personalised Assessments
Assess
November 5, 2023
Comparing Quantities | Study
Assess
Interact
Pre-Requisires
Test & Enrich
Pre – Requisite

English Version
Speed Notes
Notes For Quick Recap
Comparing Quantities: Weare often requiredto compare two quantities, in our dailylife. They may be heights, weights, salaries, marks etc. To compare two quantities, their units must be the same.
We are often required to compare two quantities in our daily life. They may be heights, weights,salaries, marks etc. (Scroll down to continue …)
Study Tools
Audio, Visual & Digital Content
While comparing heights of two persons with heights150 cm and 75 cm, we write it as the ratio 150 : 75 or 2 : 1.
Ratio: A ratio compares two quantities using a particular operation.
Percentage: Percentage are numerators of fractions with denominator 100. Percent is represent by the symbol% and means hundredth too.
Two ratios can be compared by converting them to like fractions. If the two fractions are equal,we say the two given ratios are equivalent.
If two ratios are equivalent then the four quantities are said to be in proportion. For example, the ratios 8 : 2 and 16 : 4 are equivalent therefore 8, 2, 16 and 4 are in proportion.
A way of comparing quantities is percentage. Percentages are numerators of fractions with denominator 100. Per cent means per hundred. For example 82% marks means
82 marks out of hundred.
Percentages are widely used in our daily life,
(a) We have learnt to find exact number when a certain per cent of the total quantity is given.
(b) When parts of a quantityare given to us as ratios, we have seen how to convert
them to percentages.
(c) The increase or decrease in a certainquantity can also be expressed as percentage.
(d) The profit or loss incurredin a certain transaction can be expressedin terms of percentages.
(e) While computing intereston an amount borrowed, the rate of interest is given in terms of per cents. For example, ` 800 borrowed for 3 years at 12% per annum. Simple Interest:Principal means the borrowed money.
The extra money paid by borrower for using borrowedmoney for given time is called interest(I).
The period for which the money is borrowed is called ‘TimePeriod’ (T).
Rate of interestis generally given in percentper year.
Interest, I = PTR/100
Total money paid by the borrower to the lenderis called the amount.

Hindi Version
Dig Deep
Topic Level Resources
Sub – Topics
Select A Topic
Topic:
Chapters Index
Select Another Chapter
Assessments
Personalised Assessments
Assess
November 5, 2023
Integers | Study
Assess
Interact
Pre-Requisires
Test & Enrich
Pre – Requisite

English Version
Integers | Speed Notes
Notes For Quick Recap
Integers are a bigger collection of numbers which is formed by whole numbers and their negatives. You have studied inthe earlier class, about the representation of integers onthe number lineand their addition and subtraction. (Scroll down to continue …)
Study Tools
Audio, Visual & Digital Content
We now study theproperties satisfied by addition andsubtraction.
(a) Integers are closed for addition and subtraction both. That is, a + b and a – b are again integers, where a andb are anyintegers.
(b) Addition is commutative forintegers, i.e., a + b = b + a for allintegers a andb.
(c) Addition is associative for integers, i.e., (a + b) + c = a + (b + c) for all integers a, b and c.
(d) Integer 0 is the identity under addition. That is, a + 0 = 0 + a = a for every integer a. We studied, how integers could be multiplied, andfound that product of a positive and a negative integer is a negative integer, whereas the product of two negative integers isa positive integer. For example, –2 × 7 = –14 and –3 × – 8 =24.
Product of even number of negative integers is positive, whereas the product of odd number of negative integers is negative. Integers showsome properties under multiplication.
(a) Integers are closed under multiplication. Thatis, a × b isan integer forany two integers a and b.
(b) Multiplication is commutative for integers. Thatis, a × b = b × a forany integers a and b.
(c) The integer 1 is theidentity under multiplication, i.e., 1 × a = a × 1 = a forany integer a.
(d) Multiplication is associative for integers, i.e.,(a × b) × c = a × (b × c) for anythree integers a,b and c.
Under addition and multiplication, integers show a property called distributive property.
That is, a× (b +c) = a × b+ a × c forany three integers a, b andc.
The properties of commutativity, associativity under addition and multiplication, and the distributive property help us to make our calculations easier. We alsolearn how to divide integers. We found that,
(a) When a positive integer is divided by a negative integer, the quotient obtained is a negative integer and vice-versa. (b) Division of a negative integer by another negative integer gives a positive integer as quotient. For any integer a,we have
1) The numbers. . . , —4,—3, —1, 0, 1, 2,3, 4, etc.are integers.
2) 1, 2, 3, 4, 5. . . . are positive integers and —1,-2, —3,.. are negative integers.
3) 0 isan integer which is neither positive nornegative.
4). On an integer number line, all numbers to the right of 0 arepositive integers andall numbers tothe left of0 are negative integers.
5) 0 is less than everypositive integer and greater than everynegative integer.
6) Every positive integer is greater than every negative integer.
7) Two integers thatare at thesame distance from 0, but onopposite sides of it are called opposite numbers.
8. The greater the number, the lesser is its opposite.
9. The sumof an integer and its opposite is zero.
10. The absolute valueof an integer is the numerical value of theinteger without regard to its sign.
The absolute value of an integer a isdenoted by |a| and is given by a,if a is positive or 0 a = -a,if a is negative
11. The sum oftwo integers of the same sign is an integer of the same sign whose absolute value is equal to the sum of the absolute values of the given integers.
12. The sum of two integers of opposite signs is an integer whose absolute value is the difference of the absolute values of addend and whose sign isthe sign ofthe addend having greater absolute value.
13. To subtract an integer b from another integer a, we change the sign ofb and addit to a. Thus, a − b = a + (−b)
14. All properties of operations onwhole numbers aresatisfied by theseoperations on integers.
15. If aand b are two integers, then(a − b) is alsoan integer.
16. −a and aare negative oradditive inverses of each other.
17. To find theproduct of twointegers, we multiply theirabsolute values andgive the result a plus signif both thenumbers have the same sign or a minussign otherwise.
18. To find thequotient of oneinteger divided by another non-zero integer, we divide their absolute values and give the result a plus sign if both the numbers have the same sign or a minus signotherwise.
19. All the properties applicable to wholenumbers are applicable to integers in addition, the subtraction operation has the closure property.
20. Any integer whenmultiplied or divided by 1 gives itself and whenmultiplied or divided by-1 gives its opposite.
21. When expression hasdifferent types ofoperations, some operations haveto be performed before the others. That is, each operation has its own precedence. The order in which operations are performed is division, multiplication, addition and finally subtraction (DMAS).
22. Brackets are usedin an expression when we wanta set of operations to be performed before the others.
23. While simplifying anexpression containing brackets, the operations within the innermost set of brackets are performed first and then those brackets are removed followed by the ones immediately after them tillall the brackets are removed.
24. While simplifying arithmetic expressions involving various brackets and operations, we use BODMAS rule.

Hindi Version
Dig Deep
Topic Level Resources
Sub – Topics
Select A Topic
Topic:
Chapters Index
Select Another Chapter
Assessments
Personalised Assessments
Assess
November 5, 2023
Fractions and Decimals | Study
Assess
Interact
Pre-Requisires
Test & Enrich
Pre – Requisite

English Version
Speed Notes
Notes For Quick Recap
(Scroll down to continue …)
Study Tools
Audio, Visual & Digital Content
Fractions:
4. A fraction whose numerator is less than the denominator is called a proper fraction.
5. A fraction whose numerator is more than or equal to the denominator is called animproper fraction.
6. A combination of a whole number and a proper fraction is called a mixed fraction.
7. To get a fractionequivalent to a given fraction,we multiply (or divide) its numerator and denominator by the same non-zero number.
8. Fractions having the same denominators are called like fractions. Otherwise, they are calledunlike fractions.
9. A fraction is said to be in its lowest termsif its numerator and denominator have no commonfactor other than 1.
10. To compare fractions, we use the followingsteps:
Step I Find the LCMof the denominators of the given fractions.
Step II Converteach fraction to itsequivalent fraction with denominator equal to the LCM obtained in step I.
Step Ill Arrangethe fractions in ascending or descending order byarranging numerators in ascending or descending order.
11. To convert unlike fractions into like fractions, we use the following steps:Step I Find the LCM of the denominators of the given fractions.
Step II Convert each of the given fractions into an equivalent fraction having denominator equal to the LCM obtained in step I.
12. To add (or subtract)fractions, we may use the following steps:Step I Obtain the fractionsand their denominators.
Step II Find the LCMof the denominators.
Step III Convert each fraction into an equivalent fraction having its denominator equal to the LCM obtainedin step II.
Step IV Add (or subtract) like fractions obtained in Step Ill.
Step III Convert each fraction into an equivalent fraction having its denominator equal to the LCM obtainedin step II.
Step IV Add (or subtract) like fractions obtained in Step Ill.
14. Two fractions are said to be reciprocal of each other, if their product is 1. The reciprocal of a non zero fraction a/b is b/a.
15. The divisionof a fraction a/b by a non-zero fraction c/d is the product of a/b with the
reciprocal of c/d.
Decimals:
1. Decimals are an extension of our number system.
2. Decimals are fractionswhose denominators are 10, 100, 1000 etc.
3. A decimal has two parts, namely, the whole numberpart and decimal part.
4. The number of digits containedin the decimal part of a decimal number is known as the numberof decimal places.
5. Decimals having the same number of places are called like decimals, otherwise they are knownas unlike decimals.
6. We have, 0.1 = 0.10 = 0.100 etc, 0.5 = 0.50 = 0.500 etc and so on. That is by annexing zeros on the right side of the extreme right digit of the decimalpart of a number does not alterthe value of the number.
7. Unlike decimals may be converted into like decimals by annexing the requisite numberof zeros on the right side of the extreme right digit in the decimal part.
8. Decimal numbers may be convertedby using the following steps.Step I Obtain the decimalnumbers
Step II Compare the whole partsof the numbers. The number with greater whole part will be greater. If the whole parts are equal, go to next step.
Step Ill Compare the extreme left digits of the decimal parts of two numbers. The number with greater extreme left digit will be greater. If the extreme left digits of decimal parts are equal,then compare the next digits and so on.
9. A decimal can be converted into a fractionby using the following steps:Step I: Obtain the decimal.
Step II: Take the numerator as the number obtained by removing the decimal point from the given decimal.
Step III: Take the denominator as the number obtainedby inserting as many zeros with 1 (e.g.10, 100 or 1000 etc.)as there are number of places in the decimal part.
10. Fractions can be converted into decimals by using the following steps:
Step I: Obtain the fractionand convert it into an equivalent fraction with denominator 10 or 100 or 1000 if it is not so.
Step II: Write its numeratorand mark decimal point after one place or two places or threeplaces from right towards left if the denominator is 10 or 100 or 1000 respectively. If the numerator is short of digits, insert zeros at the left of the numerator.
11. Decimals can be added or subtracted by using the following steps:Step I: Convert the given decimals to like decimals.
Step II: Write the decimals in columns with their decimal pointsdirectly below each other so that tenthscome under tenths, hundredths come and hundredths and so on.
Step III: Addor subtract as we add or subtract whole numbers.
Step IV: Place the decimal point, in the answer, directly below the other decimal points.
12. In order to multiply a decimal by 10, 100, 1000 etc., we use the following rules:
Rule I: On multiplying a decimal by 10, the decimalpoint is shiftedto the right by one place.
Rule II: On multiplying a decimal by 100, the decimal point is shiftedto the right by two places.
Rule III: On multiplying a decimal by 1000, the decimal point is shiftedto the right by threeplaces, and so on.
13. A decimal can be multiplied by a whole number by using following steps:
Step I: Multiply the decimal without the decimalpoint by the given whole number.
Step II: Mark the decimal point in the product to have as many placesof decimal as are there in the given decimal.
14. To multiply a decimal by another decimal, we follow following steps:
Step I: Multiply the two decimalswithout decimal point just like whole numbers.
Step II: Insert the decimal point in the product by countingas many places from the right to left as the sum of the number of decimalplaces of the given decimals.
15. A decimal can be dividedby 10, 100, 1000 etc by using the followingrules:
Rule I When a decimal is divided by 10, the decimal point is shifted to the left by one place.
Rule II When a decimal is divided by 100, the decimal point is shifted to the left by two places.
Rule III When a decimal is divided by 1000, the decimal point is shiftedto the left by threeplaces.
16. A decimal can be divided by a whole number by using the following steps:Step I: Check the whole number part of the dividend.
Step II: If the wholenumber part of the dividend is less than the divisor,then place a 0 in the onesplace in the quotient. Otherwise, go to step Ill.
Step III: Divide the whole number part of the dividend.
Step IV: Place the decimal point to the right of ones place in the quotient obtained in step I.
Step V: Divide the decimal part of the dividend by the divisor. If the digits of the dividend are exhausted, then place zeros to the right of dividendand remainder each time and continue the process.
17. A decimal can be divided by a decimal by using the following steps:
Step 1 Multiple the dividend and divisor by 10 or 100 or 1000 etc. to convert the divisor into a whole number.
Step II Divide the new dividendby the whole number obtainedin step I.
Extra:

Hindi Version
Dig Deep
Topic Level Resources
Sub – Topics
Select A Topic
Topic:
Chapters Index
Select Another Chapter
Assessments
Personalised Assessments
Assess
November 5, 2023
Data Handling | Study
Assess
Interact
Pre-Requisires
Test & Enrich
Pre – Requisite

English Version
Data Handling | Speed Notes
Notes For Quick Recap
The collection, recording and presentation of data help us organiseour experiences and draw inferences from them.
Before collecting data we need to know what we would use it for.
The data that is collected needs to be organised in a propertable, so that it becomeseasy to understand and interpret. (Scroll down to continue …).
Study Tools
Audio, Visual & Digital Content
Average is a numberthat represents or shows the central tendencyof a group of observations or data.
Arithmetic mean is one of the representative values of data.
Mean = sum of all observations/ Number of observations.
Mode is another form of central tendency or representative value.
The mode of a set of observations is the observation that occurs most often.
If each of the value in a data is occurring one time, then all are mode.
Sometimes we also say that this data has no mode since none of them is occurring frequently.
Median is also a form of representative value.
It refers to the value which lies in the middle of the data with half of the observations above it and the other half below it.
.
A bar graph is a representation of numbers using bars of uniform widths.
Double bar graphshelp to comparetwo collections of data at a glance.
Double bar graphshelp to comparetwo collections of data at a glance.
There are situations in our life, that are certain to happen, some that are impossible and some that may or may not happen.
The situation that may or may not happen has a chanceof happening.
Probability: A branch of mathematics that is capable of calculating the chance or likelihood of an event taking place (in percentage terms).
If you have 10 likelihoods and you want to calculate the probability of 1 event taking place,it is said that its probability is 1/10 or event has a 10% probability of taking place.
Events that have many possibilities can have probability between 0 and 1.
Important Formulae – Data Handling
1. A trial is anaction which results in one or several outcomes. 2. An experiment in whichthe result ofa trial cannot be predicted inadvance is called a random experiment.
3. An event associated to a random experiment is thecollection of someoutcomes of theexperiment.
4. An event associated witha random experiment is said tohappen if anyone of theoutcomes satisfying thedefinition of theevent is anoutcome of theexperiment when it is performed.
5. The Empirical probability ofhappening of an event E is defined as: P(E)= Number of trials in which the event happened/ Total number of trials.

Hindi Version
Dig Deep
Topic Level Resources
Sub – Topics
Select A Topic
Topic:
Chapters Index
Select Another Chapter
Assessments
Personalised Assessments
Assess
November 5, 2023
Simple Equations | Study
Assess
Interact
Pre-Requisires
Test & Enrich
Pre – Requisite

English Version
Simple Equations | Speed Notes
Notes For Quick Recap
An equation isa condition ona variable suchthat two expressions in the variable should have equalvalue.
Thevalue of thevariable for whichthe equation issatisfied is called the solution ofthe equation.
An equation remains the same if the LHSand the RHSare interchanged. (Scroll down to continue …)
Study Tools
Audio, Visual & Digital Content
In case ofthe balanced equation, if we add the same number to both thesides, or subtract the same number from both the sides,
or
multiply both sidesby the same number, or divide both sidesby the samenumber, the balance remains un disturbed,
i.e.,the value of the LHS remains equal to the value of the RHS The above property gives a systematic method of solving an equation.
We carry out a series of identical mathematical operations on the two sides of the equation in such a waythat on oneof the sides we get justthe variable. Thelast step isthe solution of the equation.
Transposing means moving to the other side.
Transposition of a number has the same effect as adding same number to (or subtracting the same number from) both sides of the equation.
Whenyou transpose a number fromone side ofthe equation tothe other side, you change itssign.
For example, transposing +3 fromthe LHS tothe RHS in equation x + 3 = 8 gives x = 8 – 3 (= 5).
We can carry out the transposition of an expression in thesame way as the transposition of a number.
We havelearnt how to construct simple algebraic expressions corresponding to practical situations.
Wealso learnt how,using the technique of doing thesame mathematical operation (for example adding the samenumber) on bothsides, we could build an equation starting fromits solution.
Further, we also learnt that we could relate a given equation tosome appropriate problem/puzzlefrom the equation. practical situation and build a practical word.

Hindi Version
Dig Deep
Topic Level Resources
Sub – Topics
Select A Topic
Topic:
Chapters Index
Select Another Chapter
Assessments
Personalised Assessments
Assess
November 5, 2023
Lines and Angles | Study
Assess
Interact
Pre-Requisires
Test & Enrich
Pre – Requisite

English Version
Speed Notes
Notes For Quick Recap
We recall that
(i) A line-segment has two end points.
(ii) A ray has only one end point (its vertex);and
(III) A line has no end points on either side.
An angle is formed when two lines (or rays or line-segments) meet.
Study Tools
Audio, Visual & Digital Content
Important Formulas | Lines and Angles
When two lines l and m meet, we say they intersect; the meeting point is calledthe point of intersection.
When lines drawnon a sheet of paper do not meet, howeverfar produced, we call them to be parallel lines.
Point: A point name a location.
Line: A line is perfectlystraight and extends forever in both direction.
Line segment: A line segmentis the part of a line betweentwo points.
Ray: A ray is part of a line that starts at one point and extendsforever in one direction.
Intersecting lines: Two or more lines that have one and only one point in common.
The common point where all the intersecting lines meet is called the point of
intersection.
Transversal: A line intersects two or more lines that lie in the same plane in distinct points.
Parallel lines: Two lineson a plane that nevermeet. They distance apart.
Complementary Angles: Two angles whose measures add to 90^O Supplementary Angles: Two angles whose measures add to 180 ^o
Adjacent Angles: Two angles have a common vertex and a
common interiorpoints.
Linear pairs: A pair of adjacentangles whose non-common sides are oppositerays. Vertically Opposite Angles: Two angles formed by two intersecting lines have common arm.
Angles made by Transversal: When two lines are intersecting by a transversal, eight anglesare formed.
Transversal of Parallel Lines: If two parallel lines are intersected by a transversal, each pair of:
Corresponding angles are congruent. Alternateinterior angles are congruent. Alternateexterior angles are congruent.
If the transversal is perpendicular to the parallellines, all of the angles formed are congruent to 90 o angles.
1. A linewhich intersects two or more given lines at distinct points is called a transversal to the given lines.
2. Lines in a plane areparallel if theydo not intersect when produced indefinitely in either direction.
3. The distance between two intersecting lines is zero.
4. The distance between two parallel lines is thesame everywhere andis equal tothe perpendicular distance between them.
5. If two parallel lines are intersected by a transversal then (i) pairs ofalternate (interior orexterior) angles are equal. (ii) pairs of corresponding angles are equal. (iii) interior angles onthe same sideof the transversal are supplementary. 6. If twonon-parallel lines areintersected by transversal then none of (i), (ii) and (iii) hold true in 5. 7. If twolines are intersected by a transversal, thenthey are parallel ifany one of thefollowing is true: (i) The angles of a pair of corresponding angles are equal. (ii) The angles of a pairof alternate interior angles are equal. (iii) The angles of a pairof interior angles on the sameside of the transversal are supplementary.

Hindi Version
Dig Deep
Topic Level Resources
Sub – Topics
Select A Topic
Topic:
Chapters Index
Select Another Chapter
Assessments
Personalised Assessments
Assess
November 5, 2023
Introduction to Graphs | Study
Assess
Interact
Pre-Requisires
Test & Enrich
Pre – Requisite

English Version
Speed Notes
Notes For Quick Recap
Graphical presentation of data is easier to understand.
A bar graph is used to show comparison among categories.
A pie graph is used to compare parts of a whole.
A Histogram is a bar graph that shows data in intervals. (Scrol down to continue …)
Study Tools
Audio, Visual & Digital Content
Introduction to Graphs
A line graph displays data that changes continuously over periods of time. A line graph which is a whole unbroken line is called a linear graph.
For fixing a point on the graph sheet we need, x-coordinate and y-coordinate.
The relation between dependent variable and
through a graph.
independent variable is shown
A Bar Graph: A pictorial representation of numerical data in the form of bars (rectangles) of uniform width with equal spacing. The length (or height) of each bar
represents the given number.
A Pie Graph: A pie graph is used to compare parts of a whole. The various
observations or components are represented by the sectors of the circle.
A Histogram: Histogram is a type of bar diagram, where the class intervals are shown on the horizontal axis and the heights of the bars (rectangles) show the frequency of the class interval, but there is no gap between the bars as there is no gap between the
class intervals.
Linear Graph: A line graph in which all the line segments form a part of a single line. Coordinates: A point in Cartesian plane is represented by an ordered pair of numbers.
Ordered Pair: A pair of numbers written in specified order.
Hindi Version
Dig Deep
Topic Level Resources
Sub – Topics
Select A Topic
Topic:
Chapters Index
Select Another Chapter
Assessments
Personalised Assessments
Assess
November 5, 2023
NUMBER SYSTEMS | Study
Assess
Interact
Pre – Requisites
Test & Enrich
Pre – Requisite

English Version
Speed Notes
Notes For Quick Coverage
Introduction to Natural Numbers
Non-negative counting numbers excluding zero are called Natural Numbers.
N = 1, 2, 3, 4, 5, ……….
Whole Numbers
All natural numbers including zero are called Whole Numbers.
W = 0, 1, 2, 3, 4, 5, ……………. (Scroll down to continue …)
Study Tools
Audio, Visual & Digital Content
Integers
All natural numbers, negative numbers and 0, together are called Integers.
Z = – 3, – 2, – 1, 0, 1, 2, 3, 4, …………..
Rational Numbers
The number ‘a’ is called Rational if it can be written in the form of r/s where ‘r’ and ‘s’ are integers and s ≠ 0,
Q = 2/3, 3/5, etc. all are rational numbers.
How to find a rational number between two given numbers?
To find the rational number between two given numbers ‘a’ and ‘b’.
Example:
Find 2 rational numbers between 4 and 5.
Solution:
To find the rational number between 4 and 5
To find another number we will follow the same process again.
Hence the two rational numbers between 4 and 5 are 9/2 and 17/4.
Remark: There could be unlimited rational numbers between any two rational numbers.
Irrational Numbers
The number ‘a’ which can’t be written in the form of p/q is called irrational. Here, p and q are integers and q ≠ 0. You can say that the numbers which are not rational are called Irrational Numbers.
Example – √7, √11 etc.
Real Numbers
All numbers including both rational and irrational numbers are called Real Numbers.
R = – 2, – (2/3), 0, 3 and √2
Real Numbers And Their Decimal Expansions
1. Rational Numbers
If the rational number is in the form of a/b, then we can get two situations by dividing a by b.
a. If the remainder becomes zero
While dividing if we get zero as the remainder after some steps then the decimal expansion of such a number is called terminating.
Example:
7/8 = 0.875
b. If the remainder does not become zero
While dividing if the decimal expansion continues and not becomes zero then it is called non-terminating or repeating expansion.
Example:
1/3 = 0.3333….
Hence, the decimal expansion of rational numbers could be terminating or non-terminating recurring and vice-versa.
2. Irrational Numbers
If we do the decimal expansion of an irrational number then it would be non –terminating non-recurring and vice-versa. i. e. the remainder does not become zero and also not repeated.
Example:
π = 3.141592653589793238……
Representing Real Numbers on the Number Line
To represent the real numbers on the number line, we use the process of successive magnification. We visualise the numbers through a magnifying glass on the number line.
Example:
Step 1: The number lies between 4 and 5, so we divide it into 10 equal parts. Now for the first decimal place, we will mark the number between 4.2 and 4.3.
Step 2: Now we will divide it into 10 equal parts again. The second decimal place will be between 4.26 and 4.27.
Step 3: Now we will again divide it into 10 equal parts. The third decimal place will be between 4.262 and 4.263.
Step 4: By doing the same process again we will mark the point at 4.2626.
Operations on Real Numbers
1. The sum, difference, product and quotient of two rational numbers will be rational.
Example:
2. If we add or subtract a rational number with an irrational number then the outcome will be irrational.
Example:
If 5 is a rational number. √7 is an irrational number. Then, 5 + √7 and 5 – √7 are irrational numbers.
3. If we multiply a non-zero rational number with an irrational number, the outcome will be irrational. If we divide a non-zero rational number with an irrational number, the outcome will also be irrational.
Example:
If 7 is a rational number and √5 is an irrational number then 7√7 and 7/√5 are irrational numbers.
4. The sum, difference, product and quotient of two irrational numbers could be rational or irrational.
Example:
Finding Roots of a Positive Real Number ‘x’ geometrically and mark it on the Number Line
To find √x geometrically
1. First, mark the distance x unit from point A on the line. This ensures that AB equals x unit.
2. From B mark a point C with the distance of 1 unit, so that BC = 1 unit.
3. Take the midpoint of AC and mark it as O. Then take OC as the radius and draw a semicircle.
4. From the point B draw a perpendicular BD which intersects the semicircle at point D.
The length of BD = √x.
To mark the position of √x on the number line, we will take AC as the number line. B will be zero. So C is point 1 on the number line.
Now we will take B as the centre and BD as the radius. We will draw the arc on the number line at point E.
Now E is √x on the number line.
Identities Related to Square Roots
If p and q are two positive real numbers
Examples:
1. Simplify
We will use the identity
2. Simplify
We will use the identity
Rationalising the Denominator
Rationalising the denominator means to convert the denominator containing a square root term into a rational number. This is done by finding the equivalent fraction of the given fraction.
For which we can use the identities of the real numbers.
Example:
Rationalise the denominator of 7/(7- √3).
Solution:
We will use the identityhere.
Laws of Exponents for Real Numbers
If we have a and b as the base and m and n as the exponents, then
1. a^m × aⁿ =a^m+n
2. (a^m)ⁿ = a^mn
4. a^mb^m = (ab)^m
5.a⁰ = 1
6. a¹ = a
7. 1/aⁿ = a^-n
Let a > 0 be a real number and n a positive integer.
Let a > 0 be a real number. Let m and n be integers. They have no common factors other than 1. Also, n > 0. Then,
Example:
Simplify the expression (2x³y⁴) (3xy⁵)².
Solution:
Here we will use the law of exponents
a^m × aⁿ =a^m+n and (a^m)ⁿ = a^mn
(2x³y⁴)(3xy⁵)²
(2x³y⁴)(3 ² x ² y¹⁰)
18. x³. x². y⁴. y¹⁰
18. x³⁺². y⁴⁺¹⁰
18x⁵y¹⁴
Here’s a simple outline for an eBook on Real Numbers:
Title: Understanding Real Numbers: A Comprehensive Guide
Table of Contents
Introduction to Real Numbers
What are Numbers?
Introduction to Real Numbers
Why Are Real Numbers Important?
Classification of Numbers
Natural Numbers
Whole Numbers
Integers
Rational Numbers
Irrational Numbers
Properties of Real Numbers
Closure Property
Commutative Property
Associative Property
Distributive Property
Identity and Inverse Elements
The Real Number Line
Concept of Number Line
Plotting Real Numbers on the Number Line
Understanding Density of Real Numbers
Rational and Irrational Numbers
Definition of Rational Numbers
Properties of Rational Numbers
Definition of Irrational Numbers
Examples of Irrational Numbers (like √2, π, e)
Proving √2 is Irrational
Decimals and Real Numbers
Finite and Infinite Decimals
Terminating and Non-Terminating Decimals
Relationship between Decimals and Fractions
Operations on Real Numbers
Addition and Subtraction
Multiplication and Division
Operations with Decimals
Operations with Irrational Numbers
Absolute Value and Real Numbers
Definition of Absolute Value
Geometric Representation on the Number Line
Properties of Absolute Value
The Concept of Infinity
Understanding Infinite Sets
Limits and Real Numbers
Approaching Infinity on the Number Line
Applications of Real Numbers
In Geometry (Pythagorean Theorem)
In Calculus (Limits, Derivatives, and Integrals)
In Daily Life (Measurements, Finance, etc.)
Advanced Topics on Real Numbers
Real Numbers in Algebra
Real Numbers and Functions
Real Numbers and Continuity
Conclusion
Summary of Key Concepts
Importance of Mastering Real Numbers
How Real Numbers Apply to Higher Mathematics
Chapter 1: Introduction to Real Numbers
What Are Numbers?
Numbers are abstract symbols used to represent quantities. Throughout history, different types of numbers have been developed to address various mathematical problems.
Introduction to Real Numbers
Real numbers are all the numbers that can be found on the number line. This includes rational numbers (such as 5, -3, and 0.75) and irrational numbers (such as √2 and π). Together, they form the building blocks of modern mathematics.
Real numbers are used to measure continuous quantities like distance, time, and weight. They are integral to the concepts of calculus, physics, engineering, and many other fields.
Why Are Real Numbers Important?
Real numbers play a critical role in mathematics. They allow us to describe the size of objects, calculate areas and volumes, and express very large or very small values. Without real numbers, much of modern science and technology would not exist.
Chapter 2: Classification of Numbers
Natural Numbers
The set of natural numbers consists of counting numbers, such as 1, 2, 3, and so on. These are the simplest type of numbers and do not include zero.
Whole Numbers
Whole numbers are like natural numbers but also include zero. Thus, the set is {0, 1, 2, 3,…}.
Integers
Integers expand on whole numbers by including negative numbers. The set of integers is {…, -3, -2, -1, 0, 1, 2, 3,…}.
Rational Numbers
Rational numbers are numbers that can be expressed as a fraction of two integers (a/b), where b ≠ 0. Examples of rational numbers include 1/2, -4, and 0.75.
Irrational Numbers
Irrational numbers cannot be expressed as a fraction of two integers. Examples include √2, π, and e. These numbers have non-repeating, non-terminating decimal expansions.
Chapter 3: Properties of Real Numbers
Closure Property
The set of real numbers is closed under addition, subtraction, multiplication, and division (except division by zero). This means that the result of any of these operations on two real numbers will always yield another real number.
Commutative Property
For any two real numbers a and b:
Addition: a + b = b + a
Multiplication: a × b = b × a
Associative Property
For any three real numbers a, b, and c:
Addition: (a + b) + c = a + (b + c)
Multiplication: (a × b) × c = a × (b × c)
Distributive Property
The distributive property connects addition and multiplication:
a × (b + c) = (a × b) + (a × c)
Hindi Version
Dig Deep
Topic Level Resources
Sub – Topics
Select A Topic
Topic:
Chapters Index
Select Another Chapter
Assessments
Personalised Assessments
Assess
November 5, 2023
LINEAR EQUATIONS IN TWO VARIABLES | Study
Assess
Interact
Pre-Requisires
Test & Enrich
Pre – Requisite

English Version
Linear Equations in Two Variables | Speed Notes
Notes For Quick Recap
Linear Equations
The equation of a straight line is the linear equation. It could be in one variable or two variables.
Linear Equation in One Variable
The equation with one variable in it is known as a Linear Equation in One Variable. (Scroll down to continue …)
Study Tools
Audio, Visual & Digital Content
The general form for Linear Equation in One Variable is px + q = s, where p, q and s are real numbers and p ≠ 0.
Example:
x + 5 = 10
y – 3 = 19
These are called Linear Equations in One Variable because the highest degree of the variable is one.
Graph of the Linear Equation in One Variable
We can mark the point of the linear equation in one variable on the number line.
x = 2 can be marked on the number line as follows –
Graph of the Linear Equation in One Variable
Linear Equation in Two Variables
An equation with two variables is known as a Linear Equation in Two Variables. The general form of the linear equation in two variables is
ax + by + c = 0
where a and b are coefficients and c is the constant. a ≠ 0 and b ≠ 0.
Example
6x + 2y + 5 = 0, etc.
Slope Intercept form
Generally, the linear equation in two variables is written in the slope-intercept form as this is the easiest way to find the slope of the straight line while drawing the graph of it.
The slope-intercept form is y = mx+c
Where m represents the slope of the line.
and c tells the point of intersection of the line with the y-axis.
Remark: If b = 0 i.e. if the equation is y = mx then the line will pass through the origin as the y-intercept is zero.
Solution of a Linear Equation
There is only one solution in the linear equation in one variable but there are infinitely many solutions in the linear equation in two variables.
As there are two variables, the solution will be in the form of an ordered pair, i.e. (x, y).
The pair which satisfies the equation is the solution to that particular equation.
Example:
Find the solution for the equation 2x + y = 7.
Solution:
To calculate the solution of the given equation we will take x = 0
2(0) + y = 7
y = 7
Hence, one solution is (0, 7).
To find another solution we will take y = 0
2x + 0 = 7
x = 3.5
So another solution is (3.5, 0).
Graph of a Linear Equation in Two Variables
To draw the graph of a linear equation in two variables, we need to draw a table to write the solutions of the given equation, and then plot them on the Cartesian plane.
By joining these coordinates, we get the line of that equation.
The coordinates which satisfy the given Equation lie on the line of the equation.
Every point (x, y) on the line is the solution x = a, y = b of the given Equation.
Any point, which does not lie on the line AB, is not a solution of Equation.
Example:
Draw the graph of the equation 3x + 4y = 12.
Solution:
To draw the graph of the equation 3x + 4y = 12, we need to find the solutions of the equation.
Let x = 0
3(0) + 4y = 12
y = 3
Let y = 0
3x + 4(0) = 12
x = 4
Now draw a table to write the solutions.
x 0 4
y 3 0
Now we can draw the graph easily by plotting these points on the Cartesian plane.
Linear Equation in Two Variables
Equations of Lines Parallel to the x-axis and y-axis
When we draw the graph of the linear equation in one variable then it will be a point on the number line.
x – 5 = 0
x = 5
This shows that it has only one solution i.e. x = 5, so it can be plotted on the number line.
But if we treat this equation as the linear equation in two variables then it will have infinitely many solutions and the graph will be a straight line.
x – 5 = 0 or x + (0) y – 5 = 0
This shows that this is the linear equation in two variables where the value of y is always zero. So the line will not touch the y-axis at any point.
x = 5, x = number, then the graph will be the vertical line parallel to the y-axis.
All the points on the line will be the solution of the given equation.
Equations of Lines Parallel to the x-axis and y-axis
Similarly if y = – 3, y = number then the graph will be the horizontal line parallel to the x-axis.

Hindi Version
Dig Deep
Topic Level Resources
Sub – Topics
Select A Topic
Topic:
Chapters Index
Select Another Chapter
Assessments
Personalised Assessments
Assess
November 5, 2023
COORDINATE GEOMETRY | Study
Assess
Interact
Pre-Requisires
Test & Enrich
Pre – Requisite

English Version
Coordinate Geometry: Cartesian Plane | Speed Notes
Notes For Quick Recap
Cartesian System
A plane formed by two number lines, one horizontal
and the other vertical, such that they intersect each
other at their zeroes, and then they form a Cartesian
Plane.
Scroll Down To Continue …
Study Tools
Audio, Visual & Digital Content
● The horizontal line is known as the x-axis and the vertical line is known
as the y-axis.
● The point where these two lines intersect each other is called the origin.
It is represented as ‘O’.
● OX and OY are the positive directions as the positive numbers lie in the
right and upward direction.
● Similarly, the left and the downward directions are the negative directions
as all the negative numbers lie there.
Quadrants of the Cartesian Plane The Cartesian plane is divided into four quadrants namely Quadrant I, Quadrant II, Quadrant III, and Quadrant IV anticlockwise from OX.
Coordinates of a Point To write the coordinates of a point we need to follow the following rules. ● Thex – coordinate of a point is marked by drawing perpendicular from the y-axis measured a length of the x-axis .It is also called the Abscissa.
They – coordinate of a point is marked by drawing a perpendicular from the x-axis measured a length of the y-axis .It is also called the Ordinate. ● While writing the coordinates of a point in the coordinate plane, the x – coordinate comes first, and then the y – coordinate. We write the coordinates in brackets. In figure, OB = CA = x coordinate (Abscissa), and CO = AB = y coordinate (Ordinate). We write the coordinate as (x, y).
Remarks:
As the origin, O has zero distance from the x-axis and the y-axis so its abscissa and ordinate are zero. Hence the coordinate of the origin is (0, 0). The relationship between the signs of the coordinates of a point and the quadrant of a point in which it lies.
Plotting a Point in the Plane if its Coordinates are Given
Steps to plot the point (2, 3) on the Cartesian plane:
● First of all, we need to draw the Cartesian plane by drawing the coordinate axes with 1 unit = 1 cm.
● To mark the x coordinates, starting from 0 moves towards the positive x-axis and counts to 2.
● To mark the y coordinate, starting from 2 moves upwards in the positive direction and counts to 3.
● Now this point is the coordinate (2, 3). Likewise, we can plot all the other points, like (-3, 1) and (-1.5,-2.5) in the figure.
Question: Are the coordinates (x, y) = (y, x)? Let x = (-4) and y = (-2) So (x, y) = (- 4, – 2) (y, x) = (- 2, – 4)
Let’s mark these coordinates on the Cartesian plane. You can see that the positions of both the points are different in the Cartesian plane. So, If x ≠ y, then (x, y) ≠ (y, x), and (x, y) = (y, x), if x = y.
Example: Plot the points (6, 4), (- 6,- 4), (- 6, 4) and (6,- 4) on the Cartesian plane.
Solution: Since both numbers 6, 4 are positive the point (6, 4) lies in the first quadrant. For x coordinate, we will move towards the right and count to 6. Then from that point go upward and count to 4. Mark that point as the coordinate (6, 4). Similarly, we can plot all the other three points.

Hindi Version
Dig Deep
Topic Level Resources
Sub – Topics
Select A Topic
Topic:
Chapters Index
Select Another Chapter
Assessments
Personalised Assessments
Assess
November 5, 2023

POLYNOMIALS | Study

Assess

Interact

Pre-Requisires

Test & Enrich

Pre – Requisite

English Version

Speed Notes

Notes For Quick Recap

Study Tools

Audio, Visual & Digital Content

Revision Notes on Polynomials

Polynomial

A polynomial is an algebraic expression that includes constants, variables, and exponents. It is the expression in which the variables have only positive integral powers.

Example

1. 4x³ + 3x² + x +3 is a polynomial in variable x.

2. 4x² + 3x^-1 – 4 is not a polynomial as it has negative power.

3. 3x^3/2+ 2x – 3 is not a polynomial. Polynomials

Polynomials are denoted by p (x), q (x), etc.
In the above polynomials, 2x², 3y, and 2 are the terms of the polynomial.
2 and 3 are the coefficients of x² and y, respectively.
x and y are the variables.
2 is the constant term, which has no variable.

Polynomials in One Variable

If there is only one variable in the expression, then this is called the polynomial in one variable.

Example

x³ + x – 4 is polynomial in variable x and is denoted by p(x).
r² + 2 is polynomial in variable r and is denoted by p(r).

Types of polynomials on the basis of the number of terms

Types of polynomials on the basis of the number of degrees

The highest value of the power of the variable in the polynomial is the degree of the polynomial.

Zeros of a Polynomial

If p(x) is a polynomial, then the number ‘a’ will be the zero of the polynomial with p(a) = 0. We can find the zero of the polynomial by equating it to zero.

Example: 1

The given polynomial is p(x) = x – 4

To find the zero of the polynomial, we will equate it to zero.

x – 4 = 0

x = 4

p(4) = x – 4 = 4 – 4 = 0

This shows that if we place 4 in place of x, we get the value of the polynomial as zero. So 4 is the zero of this polynomial. And also, we are getting the value 4 by equating the polynomial with 0.

So 4 is the zero of the polynomial or the root of the polynomial.

The root of the polynomial is basically the x-intercept of the polynomial.

If the polynomial has one root, it will intersect the x-axis at one point only, and if it has two roots, it will intersect at two points, and so on.

Example: 2

Find p (1) for the polynomial p (t) = t² – t + 1

p (1) = (1)² – 1 + 1

= 1 – 1 + 1

= 1

Remainder Theorem

We know the property of division which follows in the basic division, i.e.

Dividend = (Divisor × Quotient) + Remainder

This follows the division of polynomials.

If p(x) and g(x) are two polynomials in which the degrees of p(x) ≥ degree of g(x) and g(x) ≠ 0 are given, then we can get the q(x) and r(x) so that:

P(x) = g(x) q(x) + r(x),

where r(x) = 0 or degree of r(x) < degree of g(x).

It says that p(x) divided by g(x), gives q(x) as a quotient and r(x) as a remainder.

Let’s understand it with an example

Division of a Polynomial with a Monomial

We can see that ‘x’ is common in the above polynomial, so we can write it as

Hence, 3x²+ x + 1 and x the factors of 3x³ + x² + x.

Steps of the Division of a Polynomial with a Non –Zero Polynomial

Divide x² – 3x -10 by 2 + x

Step 1: Write the dividend and divisor in descending order, i.e., in the standard form. x² – 3x -10 and x + 2

Divide the first term of the dividend with the first term of the divisor.

x²/x = x this will be the first term of the quotient.

Step 2: Now multiply the divisor by this term of the quotient and subtract it from the dividend.

Step 3: Now the remainder is our new dividend, so we will repeat the process again by dividing the dividend by the divisor.

Step 4: – (5x/x) = – 5

Step 5:

The remainder is zero.

Hence x² – 3x – 10 = (x + 2)(x – 5) + 0

Dividend = (Divisor × Quotient) + Remainder

The Remainder Theorem says that if p(x) is any polynomial of degree greater than or equal to one and let ‘t’ be any real number and p (x) is divided by the linear polynomial x – t, then the remainder is p(t).

As we know,

P(x) = g(x) q(x) + r(x)

If p(x) is divided by (x-t) then

If x = t

P (t) = (t – t). q (t) + r = 0

To find the remainder or to check the multiple of the polynomial, we can use the remainder theorem.

Example:

What is the remainder if a⁴ + a³ – 2a² + a + 1 is divided by a – 1.

Solution:

P(x) = a⁴ + a³ – 2a² + a + 1

To find the zero of (a – 1), we need to equate it to zero.

a -1 = 0

a = 1

p (1) = (1)⁴ + (1)³ – 2(1)² + (1) + 1

= 1 + 1 – 2 + 1 + 1

= 2

So by using the remainder theorem, we can easily find the remainder after the division of the polynomial.