Your cart is currently empty!
Tag: Geometry
Cuboid And Cube
Geometry Axioms & Theorems
Cuboid And Cube
Cuboid
What is a cuboid?
Introduction To Cuboid
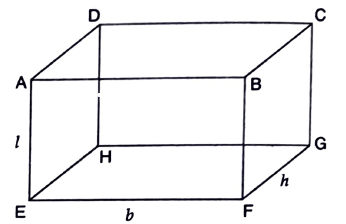
A cuboid is a three-dimensional geometric shape that resembles a rectangular box or a rectangular prism. A cuboid has 3 Pairs of opposite, congruent and parallel rectangular faces, 12 edges, and 8 vertices.
Note 1: All squares are rectangles, But All rectangles need not to be squares.
Note 2: Cuboid may have one, or three equal pairs of squares. (Square is a special type of Rectangle.
Note 3: If All one pair of opposite faces of a cuboid are squares then it it becomes an Equilateral Cuboid.
Note 3: If All three pairs of faces of a cuboid are squares then it it becomes a Cube.
Note 4: A Equilateral Cuboid and Cube is a special types of cuboid.

Parts And Their Alignment Of A Cuboid
Faces
The flat surfaces of a cuboid are known as its faces.
A cuboid has six faces, and each face is a rectangle.
These faces are arranged such that three pairs of opposite faces are parallel to each other.
The adjacent faces are perpendicular to each other (i.e., the angle between any two touching faces of a cube is right angle, 90°.
- Note 1: All squares are rectangles.
- Note 2: Rectangle may have one or two pairs of squares.
- Note 3: If All three pairs of faces of a rectangle are squares then it it becomes a Cube.
- Note 4: A cube is a special case of cuboid.
Edges
An edge is a line segment where the two surfaces of a cuboid meet.
There are 12 edges in a cuboid, where three edges meet at each vertex.
All edges form right angles with the adjacent edges and faces.
Vertices
A vertex is a point where the three edges meet. Vertices is the plural of vertex.
Cuboid has eight vertices.
Diagonals
Diagonal of a cuboid is a line segment that joins two opposite vertices.
The cuboid has four space diagonals.
Length of the diagonal of cuboid = √(length2 + breadth2 + height2) units.
Symmetry
Cuboids exhibit high symmetry.
They have rotational symmetry of order 4, meaning that you can rotate them by 90 degrees about their centre and they will look the same.
Features of a Cuboid
It is a three-dimensional, Rectangular figure.
It has 6 faces, 12 edges, and 8 vertices.
All 6 faces are rectangles.
Each vertex meets three faces and three edges.
The edges run parallel to those parallel to it.
All angles of a cuboid are right angles.
Mensuration of Cuboid
What Is Diagonal Of A Cuboid?
The diagonal of a cuboid is the line segment that connects two opposite vertices of the cuboid. In other words, it is the longest line that can be drawn inside the cuboid.
Clculating The Length Of Diagonal Of A Cuboid?
To calculate the length of the diagonal, we need to know the lengths of all three edges of the cuboid. Let’s call these edges l, w and h. The length of the diagonal is then given by the following formula:
d = √(l² + w² + h²)
For example, let’s say that we have a cuboid with edges that are all equal to two meters. In this case, the length of the diagonal would be:
d = √(l² + w² + h²)
Example: if l = 3 cm, b = 2cm, h = 1cm, Find is longest diagonal
The longest diagonal of a cuboid = d = √(l² + w² + h²)
On substituting the values we get
d = √(3² + 2² + 1²) = √(9 + 4 +1) = √14 cm
Therefore, the length of the diagonal is fourteen meters.
Surface Area of a Cuboid
The total surface area of a cuboid is defined as the area of its surface (Appearing face).
The Lateral Surface Area of a Cube.
Imagine yourself sitting in a cuboid shaped room. You can then see the four walls around you. This denotes the lateral surface area of that room.
That is, the lateral surface area of a cuboid shaped room is the area of its four walls, excluding the ceiling and the floor.
The lateral surface area of the cuboid is the sum of areas of its square faces, excluding the area of the top and the bottom face.
So the lateral surface area of a cube = sum of areas of 4 faces = (Length ✕ Height) + (Length ✕ Height) + (Length ✕ Height) + (Breadth ✕ Height) + (Breadth✕ Height)
Derivation of Total Surface Area of a Cuboid
Since the total surface area of a cuboid (TSA) is the area of its surface.
Total surface area of a cuboid = Lateral Surface Area + Area Of Bottom Surface + Area Of Top Surface
Total surface area of a cuboid = Area Of Front Surface + Area Of Back Surface + Area Of Left Srface + Area Of Right Surface + Area Of Bottom Surface + Area Of Top Surface
Total surface area of a cuboid = Lateral Surface Area 2[Area Of Bottom Surface]
Since Area Of Top Surface = + Area Of Bottom Surface We get, Total surface area of a cuboid = Lateral Surface Area + 2[Area Of Top Surface]
TSA = (Length ✕ Height) + (Length ✕ Height) + (Length ✕ Height) + (Breadth ✕ Height) + (Breadth✕ Height) + (Length ✕ Breadth) + (Length ✕ Breadth)
TSA = 2(Length ✕ Height) + 2(Breadth ✕ Height) + 2(Length ✕ Breadth)
TSA = 2[(Length ✕ Height) + (Breadth ✕ Height) + (Length ✕ Breadth)]
The Volume of a Cube
Volume
The volume of a three-dimensional object can be defined as the space required for it.
Similarly, Volume of a cuboid is defined as the space required for the cuboid or the Space occupied by the cuboid.
The volume of a cuboid can be calculated using the formula, V = lbh, where,
l = length, b = breadth or width, h = height
This formula shows that the volume of a cuboid is directly proportional to its length, breadth and height.
The volume is calculated by multiplying the object’s length, breadth, and height.
Hence the volume of the cube = lbh = lenth ✕ breadth ✕ height
Cuboids in Our Daily Life
- Cuboids are commonly used in everyday objects, such as boxes, books, and building blocks.
- They are used in architectural and engineering designs for modeling rooms, buildings, and structures.
- In mathematics and geometry, cuboids serve as fundamental examples for teaching and understanding concepts related to three-dimensional shapes.
Similar Shapes:
- A cube is a special type of cuboid where all sides are equal in length, making it a regular hexahedron.
Real-world Examples:
- A shoebox is an example of a cuboid.
- Most refrigerators, ovens, and TV screens have cuboidal shapes.
- Buildings and houses often have cuboidal rooms.
Fun Fact:
- Cuboids are among the simplest and most familiar three-dimensional shapes, making them a fundamental concept in geometry.
Remember that these notes provide an overview of cuboids, and there are more advanced topics and applications related to this shape in various fields of study.
What is a cube?
A cube is a three-dimensional regular polyhedron characterised by its 6 Identical (Congruent) Squares in which 3 Pairs of them parallel.
Parts And Their Alignment Of In A Cube
Faces
The flat surfaces of a cube are known as its faces.
A cube has six faces, and each face is a perfect square. These faces are arranged such that three pairs of faces are parallel to each other.
The adjacent faces are perpendicular to each other (the angle between any two touching faces of a cube is right angle, 90°.
All the edges have the same length.
A cube also has 8 vertices and 12 edges.
Edges
An edge is a line segment where the two surfaces of a cube meet.
There are twelve edges in a cube, where three edges meet at each vertex.
All edges have equal length and form right angles with the adjacent edges and faces.
Vertices
A vertex is a point where the three edges meet. Vertices is the plural of vertex.
Cube has eight vertices.
Diagonals
The cube has four space diagonals that connect opposite vertices, each of which has a length of √3 times the length of an edge.
Symmetry
Cubes exhibit high symmetry.
They have rotational symmetry of order 4, meaning that you can rotate them by 90 degrees about their centre and they will look the same.
Features of a Cube
It is a three-dimensional, square-shaped figure.
It has 6 faces, 12 edges, and 8 vertices.
All 6 faces are squares with equal area.
All sides have the same length.
Each vertex meets three faces and three edges.
The edges run parallel to those parallel to it.
All angles of a cube are right angles.
Mensuration of Cube
Surface Area of a Cube
The total surface area of a cube is defined as the area of its outer surface.
Derivation of Total Surface Area of a Cube
Since the total surface area of a cube is the area of its outer surface.
total surface area of a cube = 6 ✕ area of one face.
We know that the cube has six square faces and each of the square faces is of the same size, the total surface area of a cube = 6 ✕ area of one face.
Let the length of each edge is “s”.
Area of one square face = length of edge ✕ length of edge
Area of one square face == s ✕ s = s²
Therefore, the total surface area of the cube = 6s²
The total surface area of the cube will be equal to the sum of all six faces of the cube.
The Lateral Surface Area of a Cube.
Imagine yourself sitting in a cube shaped room. You can then see the four walls around you. This denotes the lateral surface area of that room.
That is, the lateral surface area of a cube shaped room is the area of its four walls, excluding the ceiling and the floor.
The lateral surface area of the cube is the sum of areas of its square faces, excluding the area of the top and the bottom face.
So the lateral surface area of a cube = sum of areas of 4 faces = 4a²
The Volume of a Cube
Volume
The volume of a three-dimensional object can be defined as the space required for it.
Similarly, Volume of a cube is defined as the space required for the cube or the Space occupied by the cube.
The volume of a cube can be calculated using the formula V = s3, where “s” represents the length of one side of the cube.
This formula shows that the volume of a cube is directly proportional to the cube of its side length.
The volume is calculated by multiplying the object’s length, breadth, and height. In the case of a cube shape, the length, width, and height are all of the same length. Let us refer to it as “s”.
Hence the volume of the cube is s ✕ s ✕ s = s³
Cubes in Our Daily Life
We encounter many cubes in our daily life such as Ice cubes, sugar cubes, dice and the building blocks used in games.
Cubes play a fundamental role in the study of geometry and serve as a basis for understanding three-dimensional space and concepts such as volume and surface area.
Also, Cubes have many applications in mathematics, engineering, architecture and art etc.
Geometry Axioms & Theorems
Class 9
LINES AND ANGLES
Axiom 1: If a rays stands on a line , then the sum of two adjacent angles so formed is 180 0
Axiom 6.2 : If the sum of two adjacent angles is 180°, then the non-common arms of the angles form a line.
Theorem 6.1 : If two lines intersect each other, then the vertically opposite angles are equal.
Axiom 6.3 : If a transversal intersects two parallel lines, then each pair of corresponding angles is equal.
Axiom 6.4 : If a transversal intersects two lines such that a pair of corresponding angles is equal, then the two lines are parallel to each other.
Theorem 6.2 : If a transversal intersects two parallel lines, then each pair of alternate interior angles is equal
Theorem 6.3 : If a transversal intersects two lines such that a pair of alternate interior angles is equal, then the two lines are parallel.
Theorem 6.4 : If a transversal intersects two parallel lines, then each pair of interior angles on the same side of the transversal is supplementary.
Theorem 6.5 : If a transversal intersects two lines such that a pair of interior angles on the same side of the transversal is supplementary, then the two lines are parallel.
Theorem 6.6 : Lines which are parallel to the same line are parallel to each other.
Theorem 6.7 : The sum of the angles of a triangle is 180º
Theorem 6.8 : If a side of a triangle is produced, then the exterior angle so formed is equal to the sum of the two interior opposite angles.
TRIANGLES:
Axiom 7.1 (SAS congruence rule) : Two triangles are congruent if two sides and the included angle of one triangle are equal to the two sides and the included angle of the other triangle
Theorem 7.1 (ASA congruence rule) : Two triangles are congruent if two angles and the included side of one triangle are equal to two angles and the included side of other triangle
Theorem 7.2 : Angles opposite to equal sides of an isosceles triangle are equal.
Theorem 7.3 : The sides opposite to equal angles of a triangle are equal
Theorem 7.4 (SSS congruence rule) : If three sides of one triangle are equal to the three sides of another triangle, then the two triangles are congruent.
Theorem 7.5 (RHS congruence rule) : If in two right triangles the hypotenuse and one side of one triangle are equal to the hypotenuse and one side of the other triangle, then the two triangles are congruent.
Theorem 7.6 : If two sides of a triangle are unequal, the angle opposite to the longer side is larger (or greater).
Theorem 7.7 : In any triangle, the side opposite to the larger (greater) angle is longer.
Theorem 7.8 : The sum of any two sides of a triangle is greater than the third side
QUADRILATERALS
Theorem 8.1 : A diagonal of a parallelogram divides it into two congruent triangles.
Theorem 8.2 : In a parallelogram, opposite sides are equal.
Theorem 8.3 : If each pair of opposite sides of a quadrilateral is equal, then it is a parallelogram.
Theorem 8.4 : In a parallelogram, opposite angles are equal.
Theorem 8.5 : If in a quadrilateral, each pair of opposite angles is equal, then it is a parallelogram.
Theorem 8.6 : The diagonals of a parallelogram bisect each other
Theorem 8.7 : If the diagonals of a quadrilateral bisect each other, then it is a parallelogram
Theorem 8.8 : A quadrilateral is a parallelogram if a pair of opposite sides is equal and parallel.
Theorem 8.9 : The line segment joining the mid-points of two sides of a triangle is parallel to the third side.
Theorem 8.10 : The line drawn through the mid-point of one side of a triangle, parallel to another side bisects the third side.
AREAS OF PARALLELOGRAMS AND TRIANGLES
Theorem 9.1 : Parallelograms on the same base and between the same parallels are equal in area.
Theorem 9.2 : Two triangles on the same base (or equal bases) and between the same parallels are
equal in area
Theorem 9.3 : Two triangles having the same base (or equal bases) and equal areas lie between the same parallels
CIRCLES
Theorem 10.1 : Equal chords of a circle subtend equal angles at the centre.
Theorem 10.2 : If the angles subtended by the chords of a circle at the centre are equal, then the chords are equal.
Theorem 10.3 : The perpendicular from the centre of a circle to a chord bisects the chord.
Theorem 10.4 : The line drawn through the centre of a circle to bisect a chord is perpendicular to the chord.
Theorem 10.5 : There is one and only one circle passing through three given non-collinear points.
Theorem 10.6 : Equal chords of a circle (or of congruent circles) are equidistant from the centre (or centres).
Theorem 10.7 : Chords equidistant from the centre of a circle are equal in length.
Theorem 10.8 : The angle subtended by an arc at the centre is double the angle subtended by it at any point on the remaining part of the circle.
Theorem 10.9 : Angles in the same segment of a circle are equal
Theorem 10.10 : If a line segment joining two points subtends equal angles at two other points lying on the same side of the line containing the line segment, the four points lie on a circle (i.e. they are concyclic).
Theorem 10.11 : The sum of either pair of opposite angles of a cyclic quadrilateral is 180º.
Theorem 10.12 : If the sum of a pair of opposite angles of a quadrilateral is 180º, the quadrilateral is cyclic.
SURFACE AREAS AND VOLUMES
Surface Area of a Cuboid = 2(lb + bh + hl) where l, b and h are respectively the three edges of the cuboid
Surface Area of a Cube = 6a2
Curved Surface Area of a Cylinder = 2πrh
Total Surface Area of a Cylinder = 2πr(r + h)
Curved Surface Area of a Cone
= 1/2 × l × 2πr = πrl
L2= r2 + h2
Total Surface Area of a Cone
= πrl + πr22 = πr(l + r)
Surface Area of a Sphere = 4 π r2
Curved Surface Area of a Hemisphere = 2πr2
Total Surface Area of a Hemisphere = 3πr2
Volume of a Cuboid = base area × height = length × breadth × height
Volume of a Cube = edge × edge × edge = a3
Volume of a Cylinder = πr22
Volume of a Cone = 1/3 πr2h
Volume of a Sphere = 4/3 3 πr3
Volume of a Hemisphere = 2/3πr3
ALGEBRA :
am × an = am+n
(am)×(an) = am+n (am)/(an) = am-n (am)n = amn (am)×(bm) = (ab)m (a0)= am-m = am/am = 1 (am)×(bn) = (ab)m+n am/bm = (a/b)m
Class 8
UNDERSTANDING QUADRILATERALS
Sum of the measures of the external angles of any polygon is 360°.
The sum of the measures of the three angles of a triangle is 180°.
A parallelogram is a quadrilateral whose opposite sides are parallel
Property: The opposite sides of a parallelogram are of equal length
Property: The opposite angles of a parallelogram are of equal measure.
Property: The adjacent angles in a parallelogram are supplementary
Property: The diagonals of a parallelogram bisect each other (at the point of their intersection, of course!)
Property: The diagonals of a rhombus are perpendicular bisectors of one another
Property: The diagonals of a rectangle are of equal length.
Property: The diagonals of a square are perpendicular bisectors of each other


MENSURATION
1. Area of (i) a trapezium = half of the sum of
the lengths of parallel sides × perpendicular distance between them.
(ii) a rhombus = half the product of its diagonals.
2. Surface area of a solid is the sum of the areas of its faces.
3. Surface area of a cuboid = 2(lb + bh + hl) a cube = 6l 2 a cylinder = 2πr(r + h)
4. Amount of region occupied by a solid is called its volume.
5. Volume of a cuboid = l × b × h a cube = l3 a cylinder = πr 2h 6.
(i) 1 cm3 = 1 mL
(ii) 1L = 1000 cm3
(iii) 1 m3 = 1000000 cm3 = 1000L
EXPONENTS AND POWERS
am × an = am+n
am / an = am-n (am)n = amn (am)×(bn) = (ab)m+n (a0)= am / am = 1 am/am = (a/b)m
Class 7
LINES AND ANGLES
sum of the measures of two angles is 90°, the angles are called complementary angles.
the sum of the measures of two angles is 180°, the angles are called supplementary angles.
These angles are such that:
(i) they have a common vertex;
(ii) they have a common arm;
(iii) the non-common arms are on either side of the common arm.
Such pairs of angles are called adjacent angles. Adjacent angles have a common vertex and a common arm but no common interior points.
A linear pair is a pair of adjacent angles whose non-common sides are opposite rays.
TRIANGLES
An exterior angle of a triangle is equal to the sum of its interior opposite angles.
Statement The total measure of the three angles of a triangle is 1800
A triangle in which all the three sides are of equal lengths is called an equilateral triangle.
A triangle in which two sides are of equal lengths is called an isosceles triangle.
1.The six elements of a triangle are its three angles and the three sides.
2.The line segment joining a vertex of a triangle to the mid point of its opposite side is called a median of the triangle. A triangle has 3 medians.
3.The perpendicular line segment from a vertex of a triangle to its opposite side is called an altitude of the triangle. A triangle has 3 altitudes.
4.An exterior angle of a triangle is formed, when a side of a triangle is produced. At each vertex, you have two ways of forming an exterior angle.
5.A property of exterior angles: The measure of any exterior angle of a triangle is equal to the sum of the measures of its interior opposite angles.
6.The angle sum property of a triangle: The total measure of the three angles of a triangle is 180°.
7. A triangle is said to be equilateral, if each one of its sides has the same length. In an equilateral triangle, each angle has measure 60°
8. A triangle is said to be isosceles, if atleast any two of its sides are of same length. The non-equal side of an isosceles triangle is called its base; the base angles of an isosceles triangle have equal measure.
9. Property of the lengths of sides of a triangle: The sum of the lengths of any two sides of a triangle is greater than the length of the third side. The difference between the lengths of any two sides is smaller than the length of the third side.
CONGRUENCE OF TRIANGLES
If two line segments have the same (i.e., equal) length, they are congruent. Also, if two line segments are congruent, they have the same length.
If two angles have the same measure, they are congruent. Also, if two angles are congruent, their measures are same.
SSS Congruence Criterion:
If under a given correspondence, the three sides of one triangle are equal to the three corresponding sides of another triangle, then the triangles are congruent.
SAS Congruence Criterion:
If under a correspondence, two sides and the angle included between them of a triangle are equal to two corresponding sides and the angle included between them of another triangle, then the triangles are congruent.
ASA Congruence Criterion:
If under a correspondence, two angles and the included side of a triangle are equal to two corresponding angles and the included side of another triangle, then the triangles are congruent.
RHS Congruence Criterion:
If under a correspondence, the hypotenuse and one side of a right-angled triangle are respectively equal to the hypotenuse and one side of another right-angled triangle, then the triangles are congruent.
1 cm2 = 100 mm2
1 m2 = 10000 cm2
1 hectare = 10000 m2