Tag: Introduction to Trigonometry y

Speed Notes

Notes For Quick Recap

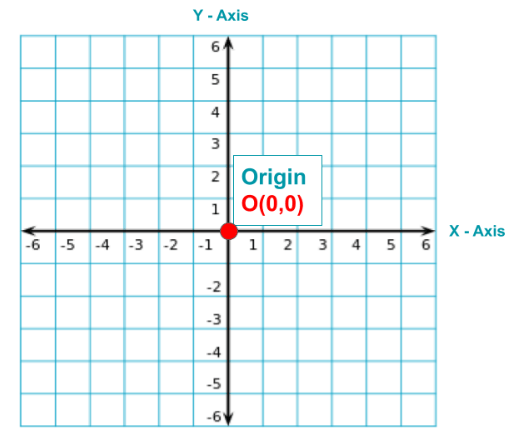
Cartesian System

A plane formed by two number lines, one horizontal

and the other vertical, such that they intersect each

other at their zeroes, and then they form a Cartesian

Plane.

Scroll Down To Continue …

Study Tools

Audio, Visual & Digital Content

Coordinate Axes:

The position of a point in a plane is fixed by selecting the axes of reference which are formed by two number lines intersecting each other at right angles, so that their zeroes coincide.

The horizontal number line is called x-axis and vertical number line is called y axis.

A point that lies on X Axis is (x,0)

A point that lies on Y Axis is (0,y)

Equation of Y Axis is x = 0

Equation of X Axis is y = 0

Equation of a lne parallel to Y Axis is x = a

Equation of a lne parallel to X Axis is y = a

Equation of a lne perpendicular to X Axis is X = a

Equation of a lne perpendicular to X Axis is X = a

The point of intersection of the two lines is called origin.

is the x-axis and Y1OY is the y-axis. These coordinate axes are also called rectangular axes as they are perpendicular to each other.

Rectangular coordinates are ordered pairs in which the first element is called the abscissa and the second element is called the ordinate.

● In the first quadrant, x is + ve and y is + ve

● In the second quadrant, x is – ve and y is + ve

● In the third quadrant, x is – ve and y is – ve

● In the fourth quadrant, x is + ve and y is -ve.

Distance Formula:

Example:

Example:

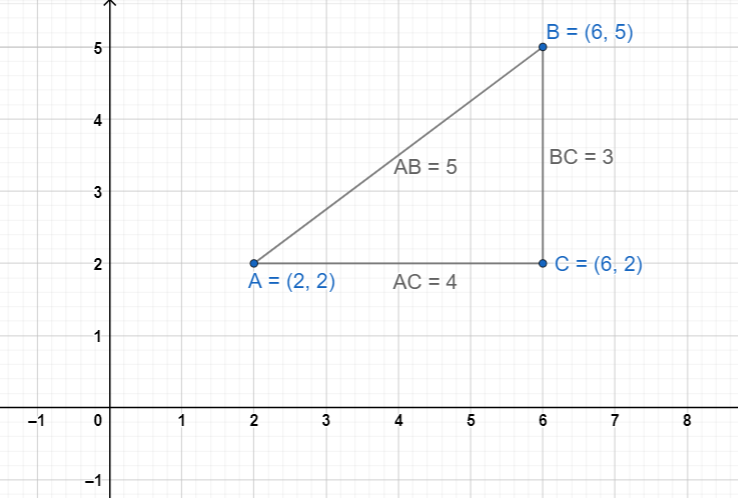
Collinearity of three points:

Three points P, Q and R are said to be collinear, if they lie in the same straight line.

i.e., PR = PQ + QR

i.e., PQ = PR + RQ

i.e., QR = QP + PR

If three points are not collinear, they always form a triangle.

Special Polygons:

(i) In Case of Triangle

(a) a right-angled triangle, if sum of squares of any two sides is equal to square of third side.

(b) an equilateral triangle, if all the three sides are equal.

(c) an isosceles triangle, if any two sides are equal.

(ii) In Case of Quadrilateral

(a) parallelogram, if opposite sides are equal and diagonals are not equal.

(b) rectangle, if opposite sides are equal and diagonals are equal.

(c) square, if all the four sides are equal and diagonals are equal.

(d) rhombus, if all the four sides are equal and diagonals are not equal.

Section Formula (Internal division only)

Midpoint Formula:

Point Dividing Two points in K : 1 Ratio:

Note:

If k is positive, the point divides the given points internally.

If k is Negative, the point divides the given points externally

Coordinates of the centroid of a triangle:

Points of Trisection:

If a line segment is divided into three equal parts by two points, the points are said to be the points of trisection.

In the given figure, the points R and S divide the line segment PQ into three equal parts i.e., PR=RS=SQ. The points R and S are said to be points of trisection.

Area of a Triangle:

The area of the triangle formed by the points

is calculated by the following expression.

Area of ∆PQR =

Area of Quadrilateral:

Area of a quadrilateral can be found by splitting up the quadrilateral into two triangles and sum up their areas.

Thus, area of quadrilateral PQRS = area of ∆PQR+ area of ∆PRS

Condition for collinearity of three points :

Three given points will be collinear, if the area of the triangle formed by these points is zero.

Rule to prove that three given points are collinear:

Step 1. Find the area of the triangle formed by the given points.

Step 2. Show that the area of the triangle formed by the given points is zero.

* The coordinates of the origin are O(0,0)

* The coordinates of any point on x-axis are (x, 0)

i.e., y=0 or ordinate is zero.

* The coordinates of any point on y – axis are (0, y) i.e., x=0 or abscissa is zero.