Your cart is currently empty!
Tag: Mensuration
MENSURATION | Study
Mensuration | Study
MENSURATION | Study
Mensuration | Study

MENSURATION | Study
Pre-Requisires
Test & Enrich
English Version Mensuration | Speed Notes
Notes For Quick Recap
Perimeter is the length of the boundary of the geometric shape.
In other words the distance covered along theboundary forming aclosed figure whenyou go round the figure once.
(a) Perimeter of arectangle = 2 × (length + breadth) (b) Perimeter of a square = 4 × length ofits side. (Scroll down to continue …)
Study Tools
Audio, Visual & Digital Content
Mensuration
Perimeter is the length of the boundary of the geometric shape.
In other words the distance covered along theboundary forming aclosed figure whenyou go round the figure once.
(a) Perimeter of arectangle = 2 × (length + breadth)
(b) Perimeter of a square = 4 × length ofits side
(c) Perimeter of anequilateral triangle =3 × length of a side
(d) Perimeter of a regular pentagon has five equal sides = 5 × length of a sides Figures in which all sides and angles are equal are called regular closed figures.
The amount of surface enclosed by a closed figure is called its area. To calculate the area of a figure using a squared paper, the following conventions are adopted :
(a) Ignore portions ofthe area thatare less thanhalf a square.
(b) If more than half a square is in a region. Count it as one square
(c) If exactly half the square is counted, take its area as
Area of a rectangle = length × breadth Area of a square = side × side
Hindi Version Dig Deep
Topic Level Resources
Sub – Topics
Select A Topic
Topic:
Chapters Index
Select Another Chapter
[display-posts category=”CBSE 6 – Mathematics – Study – Premium” posts_per_page=”25″]Assessments
Personalised Assessments

Mensuration | Study
Pre-Requisires
Test & Enrich
English Version Mensuration | Speed Notes
Notes For Quick Recap
Perimeter: Length of boundary of a simple closed figure.
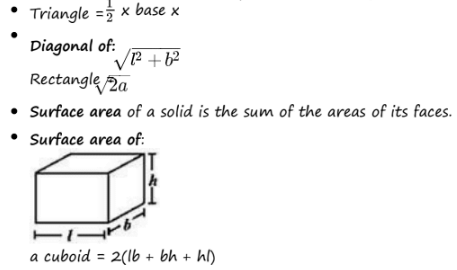
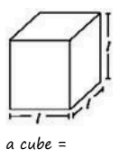
Perimeter of Rectangle = 2(l +b)
Perimeter of Square = 4a
Perimeter of Parallelogram = 2(sum of two adjacent sides)
Area: The measure of region enclosed in a simple closed figure.Area of a trapezium = half of the sum of the lengths of parallel sides × perpendiculardistance between them.
Area of a rhombus = half the product of its diagonals. (Scroll down to continue …)
Study Tools
Audio, Visual & Digital Content



Hindi Version Dig Deep
Topic Level Resources
Sub – Topics
Select A Topic
Topic:
Chapters Index
Select Another Chapter
[display-posts category=”CBSE 8 – Mathematics – Study – Premium” posts_per_page=”25″]Assessments
Personalised Assessments

MENSURATION | Study
Pre-Requisires
Test & Enrich
English Version Mensuration | Speed Notes
Notes For Quick Recap
Perimeter is the length of the boundary of the geometric shape.
In other words the distance covered along theboundary forming aclosed figure whenyou go round the figure once.
(a) Perimeter of arectangle = 2 × (length + breadth) (b) Perimeter of a square = 4 × length ofits side. (Scroll down to continue …)
Study Tools
Audio, Visual & Digital Content
Mensuration
Perimeter is the length of the boundary of the geometric shape.
In other words the distance covered along theboundary forming aclosed figure whenyou go round the figure once.
(a) Perimeter of arectangle = 2 × (length + breadth)
(b) Perimeter of a square = 4 × length ofits side
(c) Perimeter of anequilateral triangle =3 × length of a side
(d) Perimeter of a regular pentagon has five equal sides = 5 × length of a sides Figures in which all sides and angles are equal are called regular closed figures.
The amount of surface enclosed by a closed figure is called its area. To calculate the area of a figure using a squared paper, the following conventions are adopted :
(a) Ignore portions ofthe area thatare less thanhalf a square.
(b) If more than half a square is in a region. Count it as one square
(c) If exactly half the square is counted, take its area as
Area of a rectangle = length × breadth Area of a square = side × side
Hindi Version Dig Deep
Topic Level Resources
Sub – Topics
Select A Topic
Topic:
Chapters Index
Select Another Chapter
[display-posts category=”CBSE 6 – Mathematics – Study – Premium” posts_per_page=”25″]Assessments
Personalised Assessments

Mensuration | Study
Pre-Requisires
Test & Enrich
English Version Mensuration | Speed Notes
Notes For Quick Recap
Perimeter: Length of boundary of a simple closed figure.
Perimeter of Rectangle = 2(l +b)
Perimeter of Square = 4a
Perimeter of Parallelogram = 2(sum of two adjacent sides)
Area: The measure of region enclosed in a simple closed figure.Area of a trapezium = half of the sum of the lengths of parallel sides × perpendiculardistance between them.
Area of a rhombus = half the product of its diagonals. (Scroll down to continue …)
Study Tools
Audio, Visual & Digital Content



Hindi Version Dig Deep
Topic Level Resources
Sub – Topics
Select A Topic
Topic:
Chapters Index
Select Another Chapter
[display-posts category=”CBSE 8 – Mathematics – Study – Premium” posts_per_page=”25″]Assessments
Personalised Assessments