Your cart is currently empty!
Tag: Quadrilaterals
BASICS OF QUADRILATERALS | Study
QUADRILATERALS | Study

BASICS OF QUADRILATERALS | Study
Pre-Requisires
Test & Enrich
English Version Quadrilaterals | Speed Notes
Notes For Quick Recap
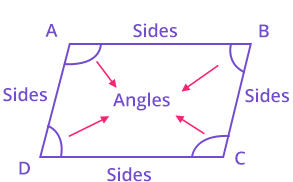
Quadrilateral
Any closed polygon with four sides, four angles and four vertices are called Quadrilateral. It could be regular or irregular. (Sroll down to continute …)

Study Tools
Audio, Visual & Digital Content
Revision Notes – CBSE 09 Math – Quadrilaterals
Quadrilaterals
A simple closed figure bounded by four line segments is called a quadrilateral, it has four sides i.e., AB, BC, CD and AD and four vertices as A, B, Can d D and the sum of all angles of a quadrilateral is 360.
Characteristics of a quadrilateral
Angle Sum Property of a Quadrilateral:
Quadrilateral is a four sided closed figure.
Sum of all angles of a quadrilateral is 360°.
Parts Of Quadrilaterals
Types Of Quadrilaterals
Classification of quadrilaterals
Quadrilaterals are broadly classified into three categories as:
(i) Kite
(ii) Trapezium
(ii) Parallelogram
Kite:
A kite is a quadrilateral with two distinct pairs of adjacent sides that are equal in length. It resembles a flying kite in shape.
🪁 Types of Kites:
There are several types of kites based on their properties:
Square Kites:
All four sides are equal in length, making it both a kite and a square.
Rhombus Kites:
All four sides are equal in length, and opposite angles are equal, making it both a kite and a rhombus.
Right Kites:
One pair of opposite angles is a right angle (90 degrees).
Equilateral Kites:
Two pairs of adjacent sides are equal, and the diagonals are perpendicular bisectors of each other.
(i) Kite has no parallel sides
(ii) Kite has a pair of equal adjacent sides.
(ii) It is not a parallelogram
Characteristics Of Kite:
Perimeter Of Kite
Area Of Kite
Trapezium:
Trapezium is a quadrilateral with the following characteristics:
(i) One pair of opposite sides is parallel to each other.
(ii) The other pair of opposite sides may not be parallel to each other.
Characteristics Of Trapezium
(i) Sum of all angles of a quadrilateral is 360°.
(ii) One pair of opposite sides is parallel to each other.
(iii) The other pair of opposite sides need not be parallel to each other.
Types Of Trapezium:
Quadrilaterals are broadly classified into two categories as:
(i) Isosceles Trapezium.
(ii) Scalene Trapezium.
(i) Right Trapezium.
Isosceles Trapezium:
Isosceles Trapezium is a quadrilateral with the following characteristics:
(i) One pair of opposite sides is parallel to each other.
(ii) The other pair of opposite sides are equal.
(iii) The other pair of opposite sides need not be parallel to each other.
Isosceles Trapezium is a trapezium with the following characteristics:
(i) One pair of opposite sides is parallel to each other.
(ii) The other pair of opposite sides are equal.
(iii) The other pair of opposite sides need not be parallel to each other.
Characteristics Of Isosceles Trapezium
(i) Sum of all angles of a quadrilateral is 360°.
(ii) One pair of opposite sides is parallel to each other.
(iii) The other pair of opposite sides are equal.
(iv) The other pair of opposite sides need not be parallel to each other.
Scalene Trapezium:
- Scalene trapezium: Classified by the length of the legs or the measurement of their angles.
Characteristics Of Scalene Trapezium
Right Trapezium:
- Right trapezium: Has one pair of parallel sides and one pair of right angles.
Characteristics Of Right Trapezium
Perimeter Of Trapezium
Area Of Trapezium
Parallelogram:
A parallelogram is a quadrilateral (a four-sided polygon) in which both pairs of opposite sides are parallel and equal in length.
In other words, Parallelogram is a quadrilateral with the following characteristics:
Characteristics of a parallelogram
Parallelogram is a quadrilateral with the following characteristics:
(i) Two pairs of opposite sides are parallel to each other.
(ii) Two pairs of opposite sides are equal in length.
(iii) Sum of all angles of a Parallelogram is 360°.
(iv) Two pairs of opposite sides are parallel to each other.
(v) Two pairs of opposite sides are equal in length.
(vi) Two pairs of opposite angles are equal.
(vii) Diagonals bisect each other.
(viii) Diagonals need not be equal to each other.
(ix) Diagonals divide it into two congruent triangles.
Types Of Parallelogram
Parallelograms are broadly classified into three categories as:
(i) Rectangle (ii) Rhombus (iii) Square
Perimeter Of Parallelogram:
Perimeter of a Parallelogram is the length of the boundary of the Parallelogram.
Perimeter of a Parallelogram = 2(length + width)
Area Of Parallelogram
Measure of the space enclosed by the boundary of a Parallelogram is called its area.
Area of a Parallelogram = Base x Height
Rectangle:
A rectangle is a Parallelogram with four right angles.
In other words, A rectangle is a quadrilateral (a four-sided polygon) in which both pairs of opposite sides are parallel and equal in length.and has four right angles.
Characteristics Of Rectangle
Rectangle is a quadrilateral with the following characteristics:
(i) Two pairs of opposite sides are parallel to each other.
(ii) Two pairs of opposite sides are equal in length.
(iii) All four angles are right angles. (each angle is 90 o).Sum of all angles of a quadrilateral is 360°.
(iv) Two pairs of opposite sides are parallel to each other.
(v) Two pairs of opposite sides are equal in length.
(vi) All four angles are right angles. (each angle is 90 o).
(vii) Diagonals bisect each other.
(viii) Diagonals are equal to each other.
(ix) Diagonals of a rectangle divide it into two congruent triangles.
Conclusions:
Every Rectangle is a Parallelogram. But Every Parallelogram need not be a Rectangle.
Condition for a rhombus to be a square:
If all four angles of a parallelogram are right angles. (each angle is 90 o), the parallelogram becomes a Rectangle.
Perimeter Of Rectangle
Perimeter of a rectangle is the length of the boundary of the rectangle.
Perimeter of a rectangle = 2(length + width)
Area Of Rectangle
Measure of the space enclosed by the boundary of a rectangle is called its area.
Area of a rectangle = length x width
Rhombus:
Rhombus is a Parallelogram with four equal sides.
In other words, A rectangle is a quadrilateral (a four-sided polygon) in which both pairs of opposite sides are parallel and equal in length.and also has four equal sides.
Characteristics Of Rhombus
Rhombus is a quadrilateral with the following characteristics:
(i) Two pairs of opposite sides are parallel to each other.
(ii) All four sides are equal in length.
(iii) Sum of all angles of a quadrilateral is 360°.
(iv) Two pairs of opposite sides are parallel to each other.
(v) All four sides are equal in length.
(vi) Two pairs of opposite angles are equal.
(vii) Diagonals bisect each other.
(viii) Diagonals need not be equal to each other.
(ix) Diagonals divide a Rhombus into two congruent triangles.
Conclusions:
Every Rhombus is a Parallelogram. But Every Parallelogram need not be a Rhombus.
Condition for a rhombus to be a square:
If all four angles of the Rhombus are right angles, the Rhombus becomes a square.
If all the sides of a parallelogram are equal, the parallelogram becomes a Rhombus.
Perimeter Of Rhombus
Perimeter of a Rhombus is the length of the boundary of the Rhombus.
Perimeter of Rhombus = 2(length + width)
Area Of Rhombus
Measure of the space enclosed by the boundary of a rhombus is called its area.
Area of Rhombus = ½(Diagonal 1 + Diagonal 2 x height)
Area of Rhombus = Base x Height
Square:
Characteristics Of Square
Square is a quadrilateral with the following characteristics:
(i) Two pairs of opposite sides are parallel to each other.
(ii) All four sides are equal in length.
(iii) All four angles are right angles. (each angle is 90 o).
(iv) Sum of all angles of a quadrilateral is 360°.
(v) Diagonals bisect each other.
(vi) Diagonals need not be equal to each other.
(vii) Diagonals divide a Rhombus into two congruent triangles.
Conclusions:
- Every square is a Rhombus. But Every Rhombus need not be a square.
Condition for a rhombus to be a square:
If all the angles of a rhombus are right angles (equal to 90o), the rhombus becomes a square.
Condition for a parallelogram to be a square:
(i) If all the angles of a parallelogram are right angles (equal to 90o), and all the sides of a parallelogram are equal in length, the parallelogram becomes a square.
Note: Every Square is a rectangle. But Every Rectangle need not be a square.
Condition for a Rectangle to be a square:
If all the sides of a Rectangle are equal in length, the Rectangle becomes a square.
Perimeter Of Square
Perimeter of a Square is the length of the boundary of the square.
Perimeter of square = 4(side)
Area Of Square
Measure of the space enclosed by the boundary of a Square is called its area.
Area of square = side2
Practical Geometry Of Quadrilaterals:
Angle Sum Property of a Quadrilateral
The sum of the four angles of a quadrilateral is 360°

If we draw a diagonal in the quadrilateral, it divides it into two triangles.
And we know the angle sum property of a triangle i.e. the sum of all the three angles of a triangle is 180°.
The sum of angles of ∆ADC = 180°.
The sum of angles of ∆ABC = 180°.
By adding both we get ∠A + ∠B + ∠C + ∠D = 360°
Hence, the sum of the four angles of a quadrilateral is 360°.
Example
Find ∠A and ∠D, if BC∥ AD and ∠B = 52° and ∠C = 60° in the quadrilateral ABCD.

Solution:
Given BC ∥ AD, so ∠A and ∠B are consecutive interior angles.
So ∠A + ∠B = 180° (Sum of consecutive interior angles is 180°).
∠B = 52°
∠A = 180°- 52° = 128°
∠A + ∠B + ∠C + ∠D = 360° (Sum of the four angles of a quadrilateral is 360°).
∠C = 60°
128° + 52° + 60° + ∠D = 360°
∠D = 120°
∴ ∠A = 128° and ∠D = 120 °.
Types of Quadrilaterals
S No. Quadrilateral Property Image 1. Trapezium One pair of opposite sides is parallel. 2. Parallelogram Both pairs of opposite sides are parallel. 3. Rectangle a. Both the pair of opposite sides is parallel.b. Opposite sides are equal.c. All the four angles are 90°. 4. Square a. All four sides are equal.b. Opposite sides are parallel.c. All the four angles are 90°. 5. Rhombus a. All four sides are equal.b. Opposite sides are parallel.c. Opposite angles are equal.d. Diagonals intersect each other at the centre and at 90°. 6. Kite Two pairs of adjacent sides are equal. Remark: A square, Rectangle and Rhombus are also a parallelogram.
Properties of a Parallelogram
Theorem 1: When we divide a parallelogram into two parts diagonally then it divides it into two congruent triangles.

∆ABD ≅ ∆CDB
Theorem 2: In a parallelogram, opposite sides will always be equal.

Theorem 3: A quadrilateral will be a parallelogram if each pair of its opposite sides will be equal.

Here, AD = BC and AB = DC
Then ABCD is a parallelogram.
Theorem 4: In a parallelogram, opposite angles are equal.

In ABCD, ∠A = ∠C and ∠B = ∠D
Theorem 5: In a quadrilateral, if each pair of opposite angles is equal, then it is said to be a parallelogram. This is the reverse of Theorem 4.
Theorem 6: The diagonals of a parallelogram bisect each other.

Here, AC and BD are the diagonals of the parallelogram ABCD.
So the bisect each other at the centre.
DE = EB and AE = EC
Theorem 7: When the diagonals of the given quadrilateral bisect each other, then it is a parallelogram.
This is the reverse of the theorem 6.
The Mid-point Theorem
1. If a line segment joins the midpoints of the two sides of the triangle then it will be parallel to the third side of the triangle.

If AB = BC and CD = DE then BD ∥ AE.
2. If a line starts from the midpoint of one line and that line is parallel to the third line then it will intersect the midpoint of the third line.

If D is the midpoint of AB and DE∥ BC then E is the midpoint of AC.
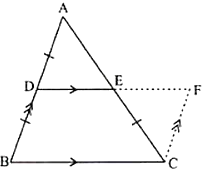
Example
Prove that C is the midpoint of BF if ABFE is a trapezium and AB ∥ EF.D is the midpoint of AE and EF∥ DC.

Solution:
Let BE cut DC at a point G.
Now in ∆AEB, D is the midpoint of AE and DG ∥ AB.
By midpoint theorem, G is the midpoint of EB.
Again in ∆BEF, G is the midpoint of BE and GC∥ EF.
So, by midpoint theorem C is the midpoint of BF.
Hence proved.
Hindi Version Dig Deep
Topic Level Resources
Sub – Topics
Select A Topic
Topic:
Chapters Index
Select Another Chapter
Assessments
Personalised Assessments

QUADRILATERALS | Study
Pre-Requisires
Test & Enrich
English Version Quadrilaterals | Speed Notes
Notes For Quick Recap
Quadrilateral
Any closed polygon with four sides, four angles and four vertices are called Quadrilateral. It could be regular or irregular. (Sroll down to continute …)
Study Tools
Audio, Visual & Digital Content
Revision Notes – CBSE 09 Math – Quadrilaterals
Angle Sum Property of a Quadrilateral
The sum of the four angles of a quadrilateral is 360°
If we draw a diagonal in the quadrilateral, it divides it into two triangles.
And we know the angle sum property of a triangle i.e. the sum of all the three angles of a triangle is 180°.
The sum of angles of ∆ADC = 180°.
The sum of angles of ∆ABC = 180°.
By adding both we get ∠A + ∠B + ∠C + ∠D = 360°
Hence, the sum of the four angles of a quadrilateral is 360°.
Example
Find ∠A and ∠D, if BC∥ AD and ∠B = 52° and ∠C = 60° in the quadrilateral ABCD.
Solution:
Given BC ∥ AD, so ∠A and ∠B are consecutive interior angles.
So ∠A + ∠B = 180° (Sum of consecutive interior angles is 180°).
∠B = 52°
∠A = 180°- 52° = 128°
∠A + ∠B + ∠C + ∠D = 360° (Sum of the four angles of a quadrilateral is 360°).
∠C = 60°
128° + 52° + 60° + ∠D = 360°
∠D = 120°
∴ ∠A = 128° and ∠D = 120 °.
Types of Quadrilaterals
S No. Quadrilateral Property Image 1. Trapezium One pair of opposite sides is parallel. 2. Parallelogram Both pairs of opposite sides are parallel. 3. Rectangle a. Both the pair of opposite sides is parallel.b. Opposite sides are equal.c. All the four angles are 90°. 4. Square a. All four sides are equal.b. Opposite sides are parallel.c. All the four angles are 90°. 5. Rhombus a. All four sides are equal.b. Opposite sides are parallel.c. Opposite angles are equal.d. Diagonals intersect each other at the centre and at 90°. 6. Kite Two pairs of adjacent sides are equal. Remark: A square, Rectangle and Rhombus are also a parallelogram.
Properties of a Parallelogram
Theorem 1: When we divide a parallelogram into two parts diagonally then it divides it into two congruent triangles.
∆ABD ≅ ∆CDB
Theorem 2: In a parallelogram, opposite sides will always be equal.
Theorem 3: A quadrilateral will be a parallelogram if each pair of its opposite sides will be equal.
Here, AD = BC and AB = DC
Then ABCD is a parallelogram.
Theorem 4: In a parallelogram, opposite angles are equal.
In ABCD, ∠A = ∠C and ∠B = ∠D
Theorem 5: In a quadrilateral, if each pair of opposite angles is equal, then it is said to be a parallelogram. This is the reverse of Theorem 4.
Theorem 6: The diagonals of a parallelogram bisect each other.
Here, AC and BD are the diagonals of the parallelogram ABCD.
So the bisect each other at the centre.
DE = EB and AE = EC
Theorem 7: When the diagonals of the given quadrilateral bisect each other, then it is a parallelogram.
This is the reverse of the theorem 6.
The Mid-point Theorem
1. If a line segment joins the midpoints of the two sides of the triangle then it will be parallel to the third side of the triangle.
If AB = BC and CD = DE then BD ∥ AE.
2. If a line starts from the midpoint of one line and that line is parallel to the third line then it will intersect the midpoint of the third line.
If D is the midpoint of AB and DE∥ BC then E is the midpoint of AC.
Example
Prove that C is the midpoint of BF if ABFE is a trapezium and AB ∥ EF.D is the midpoint of AE and EF∥ DC.
Solution:
Let BE cut DC at a point G.
Now in ∆AEB, D is the midpoint of AE and DG ∥ AB.
By midpoint theorem, G is the midpoint of EB.
Again in ∆BEF, G is the midpoint of BE and GC∥ EF.
So, by midpoint theorem C is the midpoint of BF.
Hence proved.
Hindi Version Dig Deep
Topic Level Resources
Sub – Topics
Select A Topic
Topic:
Chapters Index
Select Another Chapter
Assessments
Personalised Assessments