Your cart is currently empty!

21st Century Pedagogy | Tools & Tuitions For Learners And Educators.
Share/AssignMind Map Overal Idea Content Speed Notes Quick Coverage Content : (Scroll down till end of the page) Study Tools Audio, Visual & Digital Content Speed Notes Quick Coverage Introduction To Trigonometry | Speed Notes Notes For Quick Recap An angle is positive if its rotation is in the anticlockwise and negative if its rotation…
Personalised Teaching & Learning.
Study | Assess | Interact
Select Your Choice Of Educational Tool .
Share/AssignMind Map Overal Idea Content Speed Notes Quick Coverage Content : (Scroll down till end of the page) Study Tools Audio, Visual & Digital Content Speed Notes Quick Coverage Introduction To Trigonometry | Speed Notes Notes For Quick Recap An angle is positive if its rotation is in the anticlockwise and negative if its rotation… readmore
Mind Map
Overal Idea
Content
Speed Notes
Quick Coverage
Content : (Scroll down till end of the page)
Study Tools
Audio, Visual & Digital Content
Speed Notes
Quick Coverage
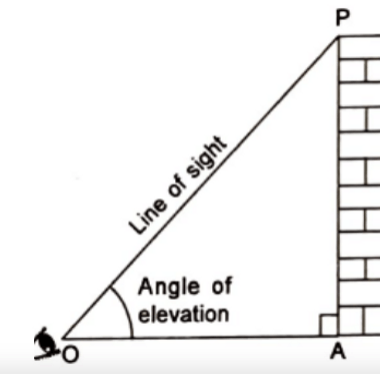
Introduction To Trigonometry | Speed Notes
Notes For Quick Recap
An angle is positive if its rotation is in the anticlockwise and negative if its rotation is in the clockwise direction.

(Scroll down to continue …)
Study Tools
Audio, Visual & Digital Content


Trigonometric Ratios

If one of the trigonometric ratios of an acute angle is known, the remaining trigonometric ration of the angle can be determined.
Two angles are said to be complementary, if their sum is 900 and each one of them is called the complement of the other.
sin (900 – θ) = Cos θ
Cos (900– θ)= Sin θ
tan (900– θ) = Cot θ
Cot(900– θ) = tan θ
sec (900– θ)= cosec θ
cosec (900– θ) = sec θ
Trigonometric Identities
An equation with trigonometric ratios of an angle θ, which is true for all values of ‘ θ ‘, for which the given trigonometric ratios are defined, is called an identity.
The three fundamental trigonometric identities are

- sin2 θ +cos2 θ = 1
⇒ sin2 θ =1-cos2 θ
⇒ sin2 θ =(1-cos θ)(1+cos θ)
⇒ (1- cos θ) = (sin2 θ) /(1+ cos θ)
⇒ (1+ cos θ) = (sin2 θ) /(1- cos θ)
⇒ cos2 θ + sin2 θ = 1
cos2 θ =1- sin2 θ
⇒ cos2 θ =(1- sin θ)(1+ sin θ)
⇒ (1+ sin θ) = (cos2 θ) /(1- sin θ)
⇒ (1- sin θ) = cos2 θ /(1+sin θ)
(b) sec2 θ = 1 + tan2 θ
⇒ sec2 θ – tan2 θ =1
⇒ (sec θ – tan θ)(sec θ + tan θ) = 1
⇒ (sec θ – tan θ) = 1/ (sec θ + tan θ)
⇒ (sec θ + tan θ) = 1/ (sec θ – tan θ)
⇒ sec2 θ – 1 = tan2 θ
⇒ (sec θ – 1)( sec θ – 1) = tan2 θ
(c) cosec2 θ = 1+cot2θ
⇒ cosec2 θ – cot2 θ = 1
⇒ (cosec θ – cot θ)(cosec θ + cot θ)=1
(cosec θ+ cot θ) =1cosec θ – cot θ
(cosec θ- cot θ) = 1cosec θ + cot θ
⇒ Cosec2 θ – 1 = cot2 θ
⇒ (Cosec θ – 1)( Cosec θ – 1) = Cot2 θ
Supportive Formulae:
(a+b)2=+a2+b2+2ab
(a-b)2 = a2+b2-2ab
(a+b)2+(a-b)2= 2 (a2+b2)
(a+b)2– (a-b)2= 4ab
(a-b)2– (a+b)2= – 4ab
(a+b)2 = (a-b)2+ 4ab
(a-b)2 = (a+b)2– 4ab
(a2-b2)=(a+b)(a-b)
a+b=(a2-b2) /(a-b)
a-b=(a2-b2) /(a-b)
(a+b)2= (a-b)2+ 4ab
Key Terms
Topic Terminology
Term
Important Tables
Table:
.
Dig Deep
Deep Learning And Testing
Here you can switch between educational tools ( Study & Assess) By Filtering Or Search for Title.





Leave a Reply
You must be logged in to post a comment.