Your cart is currently empty!
Share/AssignMind Map Overal Idea Content Speed Notes Quick Coverage Basic terms and Definitions 1. Point – A Point is that which has no component. It is represented by a dot. 2. Line – When we join two distinct points then we get a line. A line has no endpoints; it can be extended on both… readmore
Mind Map
Overal Idea
Content
Speed Notes
Quick Coverage
Basic terms and Definitions
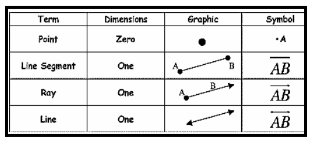
1. Point – A Point is that which has no component. It is represented by a dot.
2. Line – When we join two distinct points then we get a line. A line has no endpoints; it can be extended on both sides infinitely.
3. Line Segment Line – Segment is the part of the line which has two endpoints.
4. Ray – Ray is also a part of the line that has only one endpoint and has no end on the other side.
5. Collinear points: Points lying on the same line are called Collinear Points.
6. Non-collinear points: Points which do not lie on the same line are called Non-Collinear Points. (Scroll to continue …)
(Scroll down till end of the page)
Study Tools
Audio, Visual & Digital Content
Angles
When two rays begin from the same endpoint then they form an Angle. The two rays are the arms of the angle and the endpoint is the vertex of the angle.
Types of Angles
| Angle | Notation | Image |
| Acute | An angle which is between 0° and 90°. | |
| Right | An angle which is exactly equal to 90°. | |
| Obtuse | An angle which is between 90° and 180°. | |
| Reflex | An angle which is between 180° and 360° | |
| Straight | An angle which is exactly equal to 180°. | |
| Complete | An angle which is exactly equal to 360°. |
Complementary and Supplementary Angles
Complementary Angles are the different angles whose sum is 90°.
Complementary Angles are the different angles whose sum is 180°.

Intersecting Lines and Non-intersecting Lines
There are two ways to draw two lines-
1. The lines which cross each other from a particular point are called Intersecting Lines.
2. The lines which never cross each other at any point are called Non-intersecting Lines. These lines are called Parallel Lines and the common length between two lines is the distance between parallel lines.
Pairs of Angles Axioms
1. If a ray stands on a line, then the sum of two adjacent angles formed by that ray is 180°.
This shows that the common arm of the two angles is the ray which is standing on a line and the two adjacent angles are the linear pair of the angles. As the sum of two angles is 180° so these are supplementary angles too.
2. If the sum of two adjacent angles is 180°, then the arms which are not common of the angles form a line.
This is the reverse of the first axiom which says that the opposite is also true.
Vertically opposite Angles Theorem
When two lines intersect each other, then the vertically opposite angles so formed will be equal.
AC and BD are intersecting each other so ∠AOD = ∠BOC and ∠AOB = DOC.
Parallel Lines and a Transversal
If a line passes through two distinct lines and intersects them at distant points then this line is called Transversal Line.
Here line “l” is transversal of line m and n.
Exterior Angles – ∠1, ∠2, ∠7 and ∠8
Interior Angles – ∠3, ∠4, ∠5 and ∠6
Pairs of angles formed when a transversal intersects two lines-
1. Corresponding Angles:
- ∠ 1 and ∠ 5
- ∠ 2 and ∠ 6
- ∠ 4 and ∠ 8
- ∠ 3 and ∠ 7
2. Alternate Interior Angles:
- ∠ 4 and ∠ 6
- ∠ 3 and ∠ 5
3. Alternate Exterior Angles:
- ∠ 1 and ∠ 7
- ∠ 2 and ∠ 8
4. Interior Angles on the same side of the transversal:
- ∠ 4 and ∠ 5
- ∠ 3 and ∠ 6
Transversal Axioms
1. If a transversal intersects two parallel lines, then
- Each pair of corresponding angles will be equal.
- Each pair of alternate interior angles will be equal.
- Each pair of interior angles on the same side of the transversal will be supplementary.
2. If a transversal intersects two lines in such a way that
- Corresponding angles are equal then these two lines will be parallel to each other.
- Alternate interior angles are equal then the two lines will be parallel.
- Interior angles on the same side of the transversal are supplementary then the two lines will be parallel.
Lines Parallel to the Same Line
If two lines are parallel with a common line then these two lines will also be parallel to each other.
As in the above figure if AB ∥ CD and EF ∥ CD then AB ∥ EF.
Angle Sum Property of a Triangle
1. The sum of the angles of a triangle is 180º.
∠A + ∠B + ∠C = 180°
2. If we produce any side of a triangle, then the exterior angle formed is equal to the sum of the two interior opposite angles.
∠BCD = ∠BAC + ∠ABC.
Key Terms
Topic Terminology
Term
Important Tables
Table:
.
Dig Deep
Deep Learning And Testing
Here you can switch between educational tools ( Study & Assess) By Filtering Or Search for Title.






Leave a Reply
You must be logged in to post a comment.