Your cart is currently empty!
Tag: CBSE 10
Some Applications of Trigonometry | Material
Circles | Material
Surface Areas and Volumes | Material
Statistics | Material
Probability | Material

Some Applications of Trigonometry | Material
Pre-Requisires
Test & Enrich
English Version Some Applications Of Trigonometry | Speed Notes
Notes For Quick Recap
Introduction :
One of the main applications of trigonometry is to find the distance between two or more than two places or to find the height of the object or the angle subtended by any object at a given point without actually measuring the distance or heights or angles.
Study Tools
Audio, Visual & Digital Content
Trigonometry is useful to astronomers, navigators, architects and surveyors etc. in solving problems related to heights and distances.
The directions of the objects can be described by measuring :
(i) angle of elevation and (ii) angle of depression
Angles of elevation or angles of depression of the objects are measured by an instrument called The odolite.
The odolite is based on the principles of trigonometry, which is used for measuring angles with a rotating telescope.
In 1856, Sir George Everest first used the giant theodolite, which is now on display in the Museum of the survey of India in Dehradun.
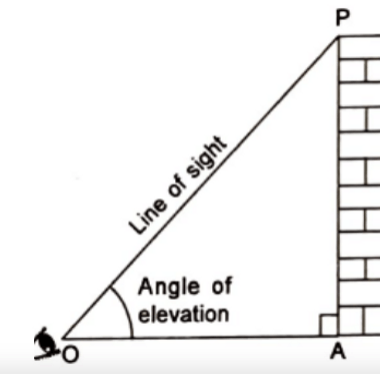
Angle of Elevation:

Let P be the position of the object above the horizontal line OA and O be the eye of the observer, then angle AOP is called angle of elevation. It is called the angle of elevation, because the observer has to elevate (raise) his line of sight from the horizontal OA to see the object P. [ When the eye turns upwards above the horizontal line.]
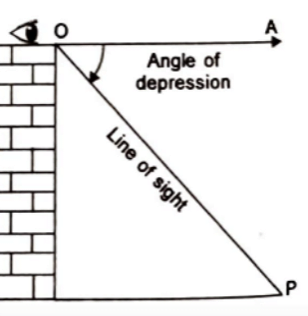
Angle of Depression:

Let P be the position of the object below the horizontal line OA and O be the eye of the observer, then angle AOP is called angle of depression.
It is called the angle of depression because the observer has to depress (lower) his line of sight from the horizontal OA to see the object P.
[When the eye turns downwards below the horizontal line].
Hindi Version Dig Deep
Topic Level Resources
Sub – Topics
Select A Topic
Topic:
Chapters Index
Select Another Chapter
Assessments
Personalised Assessments

Circles | Material
Pre-Requisires
Test & Enrich
English Version Speed Notes
Notes For Quick Recap
Study Tools
Audio, Visual & Digital Content

Circle:
Circle is a round shaped figure has no corners or edges.
A circle is the locus of all points in a plane which are at constant distance
(called radius) from a fixed point (called centre). A circle with centre O and radius r is denoted by C (O, r).
Radius:
A line segement that joins the centre and circumference or boundary of the circles is called the radius of the circles.
A line segement that divides the circle into two halves is called he diameter of the circle.
Diameter = 2x radius
Radius = Diameter/2
Chord:
A line segment joining any two points on a circle. The largest chord of a circle is a diameter.
Position of A point With Respect To a Circle:
In a plane a point P can lie either inside, or on the circle or outside the given circle.
Position of A Line With Respect to A Circle
If a circle C(O, r) and a straight line ‘l’ are in the same plane, then only three possibilities are there. These are :
Outside The Circle:
(i) The line ‘l’ does not intersect the circle at all. The line ‘l’ is called a non-intersecting line with respect to the circle.
Inside of the Circle – Secant To A Circle:
The line ‘ l ‘ intersects the circle in two distinct points say A and B. The line which intersects the circle in two distinct points is called a secant line.
Touching The Circle – Tangent To Circle:
A tangent to a circle is a special case of the secant when the two end points of the corresponding chord are coincide.
That is the line ‘ l ‘ touches the circle in only one point. Such a line which touches the circle only in one point is called a tangent line.
Tangent To Circle :
Etimology of Tangent:
The word ‘tangent’ comes from the Latin word ‘tangere’, which means to touch and was introduced by the Danish mathematician Thomas Fincke in 1583.
Tangent is a line that intersects the circle in exactly one point.
A tangent to a circle is the limiting position of a secant when its two points of intersection with the circle coincide.
The common point of the circle and the tangent is called the point of contact.
In other words the point, at which the tangent touches the circle is called
the point of contact.
Number of Tangents From A Point To Circle:
Number of tangents to a circle from a point (say P) depends upon the position of the point P.
(a)
When point ‘P’ lies outside the circle: There are only two lines, which touch the circle in one point only, all the remaining lines either intersect in two points or do not intersect the, circle. Hence, there are only two tangents from point P to the circle.
(b)
When point ‘ P ‘ lies on the circle : There is only one line which touches the circle in one point, all other lines meet the circle in more than one point. Hence, there is one and only one tangent to the circle through the point P lies on the circle.
(c)
When point ‘ P ‘ lies inside the circle: Every line passing through the point P (lies inside the circle) intersect the circle in two points. Hence, there is no tangent through the point P lies inside the circle
There is only one tangent at a point on the circumference of the circle.
Point of contact is the common point of the tangent and the circle.
The tangent at any point of a circle is perpendicular to the radius through the point of
contact.
Theorems :
(i) Tangent-Radius Theorem
The line perpendicular to the tangent and passing through the point of contact, is known as the normal.
Statement: The tangent at any point of a circle is perpendicular to the radius through the point of contact.
The converse of above theorem is also true.
Theorem :
The tangents at any point of a circle is perpendicular to the radius through the point of contact. Or At the point of contact the angle between radius and tangents to a circle is 90^0 .
Theorem :
The length of tangents drawn from an external point to a circle are equal.
Important Results:
If two circles touch internally or externally, the point of contact lies on the straight line through the two centres.
The tangent at any point of a circle is perpendicular to the radius through the point of contact.
The length of the tangents drawn from an external point to a circle are equal.
- Length of the tangent from a point P’ lies outside the circle is given by
PT =PT’ =
The distances between two parallel tangents drawn to a circle is equal to the diameter of the circle.
Facts:
In two concentric circles, the chord of the larger circle, which touches the smaller circle, is bisected at the point of contact.
More Points To Remember !
There is no tangent to a circle passing through a point lying inside the circle.
At any point on the circle there can be one and only one tangent.
The tangent at any point of a circle is perpendicular to the radius through the point of contact.
There are exactly two tangents to a circle through a point outside the circle.
The length of the segment of the tangent from the external point P and the point of contact with the circle is called the length of the tangent.
The lengths of the tangents drawn from an external point to a circle are equal.
The line containing the radius through the point of contact of tangent is called the normal to the circle at the point.
There is no tangent to the circle passing through a point lying inside the cirele.
There are exactly two tangents to a cirele through a point lying outside the circle
The length of the segment of the tangent from the external point and the point of contact
with the circle is called the length of the tangent.
The length of tangents drawn from an external point to a circle are equal.
Hindi Version Dig Deep
Topic Level Resources
Sub – Topics
Select A Topic
Topic:
Chapters Index
Select Another Chapter
Assessments
Personalised Assessments

Surface Areas and Volumes | Material
Pre-Requisires
Test & Enrich
English Version Speed Notes
Notes For Quick Recap
Cuboid
What is a cuboid?
- A cuboid is a three-dimensional geometric shape that resembles a rectangular box or a rectangular prism. A cuboid has 3 Pairs of opposite, congruent and parallel rectangular faces, 12 edges, and 8 vertices.
- Note 1: All squares are rectangles.
- Note 2: Cuboid may have one, or Three equal pairs of squares. (Square is a special type of Rectangle.
- Note 3: If All three pairs of faces of a cuboid are squares then it it becomes a Cube.
- Note 4: A cube is a special case of cuboid.
Parts And Their Alignment Of A Cuboid
Faces
The flat surfaces of a cuboid are known as its faces.
A cuboid has six faces, and each face is a rectangle.
These faces are arranged such that three pairs of opposite faces are parallel to each other.
The adjacent faces are perpendicular to each other (i.e., the angle between any two touching faces of a cube is right angle, 90°.
- Note 1: All squares are rectangles.
- Note 2: Rectangle may have one or two pairs of squares.
- Note 3: If All three pairs of faces of a rectangle are squares then it it becomes a Cube.
- Note 4: A cube is a special case of cuboid.
Edges
An edge is a line segment where the two surfaces of a cuboid meet.
There are 12 edges in a cuboid, where three edges meet at each vertex.
All edges form right angles with the adjacent edges and faces.
Vertices
A vertex is a point where the three edges meet. Vertices is the plural of vertex.
Cuboid has eight vertices.
Diagonals
Diagonal of a cuboid is a line segment that joins two opposite vertices.
The cuboid has four space diagonals.
Length of the diagonal of cuboid = √(length2 + breadth2 + height2) units.
Symmetry
Cuboids exhibit high symmetry.
They have rotational symmetry of order 4, meaning that you can rotate them by 90 degrees about their centre and they will look the same.
Features of a Cuboid
It is a three-dimensional, Rectangular figure.
It has 6 faces, 12 edges, and 8 vertices.
All 6 faces are rectangles.
Each vertex meets three faces and three edges.
The edges run parallel to those parallel to it.
All angles of a cuboid are right angles.
Mensuration of Cuboid
Surface Area of a Cuboid
The total surface area of a cuboid is defined as the area of its surface (Appearing face).
The Lateral Surface Area of a Cube.
Imagine yourself sitting in a cuboid shaped room. You can then see the four walls around you. This denotes the lateral surface area of that room.
That is, the lateral surface area of a cuboid shaped room is the area of its four walls, excluding the ceiling and the floor.
The lateral surface area of the cuboid is the sum of areas of its square faces, excluding the area of the top and the bottom face.
So the lateral surface area of a cube = sum of areas of 4 faces = (Length ✕ Height) + (Length ✕ Height) + (Length ✕ Height) + (Breadth ✕ Height) + (Breadth✕ Height)
Derivation of Total Surface Area of a Cuboid
Since the total surface area of a cuboid (TSA) is the area of its surface.
Total surface area of a cuboid = Lateral Surface Area + Area Of Bottom Surface + Area Of Top Surface
Total surface area of a cuboid = Area Of Front Surface + Area Of Back Surface + Area Of Left Srface + Area Of Right Surface + Area Of Bottom Surface + Area Of Top Surface
Total surface area of a cuboid = Lateral Surface Area 2[Area Of Bottom Surface]
Since Area Of Top Surface = + Area Of Bottom Surface We get, Total surface area of a cuboid = Lateral Surface Area + 2[Area Of Top Surface]
TSA = (Length ✕ Height) + (Length ✕ Height) + (Length ✕ Height) + (Breadth ✕ Height) + (Breadth✕ Height) + (Length ✕ Breadth) + (Length ✕ Breadth)
TSA = 2(Length ✕ Height) + 2(Breadth ✕ Height) + 2(Length ✕ Breadth)
TSA = 2[(Length ✕ Height) + (Breadth ✕ Height) + (Length ✕ Breadth)]
The Volume of a Cube
Volume
The volume of a three-dimensional object can be defined as the space required for it.
Similarly, Volume of a cuboid is defined as the space required for the cuboid or the Space occupied by the cuboid.
The volume of a cuboid can be calculated using the formula, V = lbh, where,
l = length, b = breadth or width, h = height
This formula shows that the volume of a cuboid is directly proportional to its length, breadth and height.
The volume is calculated by multiplying the object’s length, breadth, and height.
Hence the volume of the cube = lbh = lenth ✕ breadth ✕ height
Cuboids in Our Daily Life
- Cuboids are commonly used in everyday objects, such as boxes, books, and building blocks.
- They are used in architectural and engineering designs for modeling rooms, buildings, and structures.
- In mathematics and geometry, cuboids serve as fundamental examples for teaching and understanding concepts related to three-dimensional shapes.
Similar Shapes:
- A cube is a special type of cuboid where all sides are equal in length, making it a regular hexahedron.
Real-world Examples:
- A shoebox is an example of a cuboid.
- Most refrigerators, ovens, and TV screens have cuboidal shapes.
- Buildings and houses often have cuboidal rooms.
Fun Fact:
- Cuboids are among the simplest and most familiar three-dimensional shapes, making them a fundamental concept in geometry.
Remember that these notes provide an overview of cuboids, and there are more advanced topics and applications related to this shape in various fields of study.
What is a cube?
A cube is a three-dimensional regular polyhedron characterised by its 6 Identical (Congruent) Squares in which 3 Pairs of them parallel.
Parts And Their Alignment Of In A Cube
Faces
The flat surfaces of a cube are known as its faces.
A cube has six faces, and each face is a perfect square. These faces are arranged such that three pairs of faces are parallel to each other.
The adjacent faces are perpendicular to each other (the angle between any two touching faces of a cube is right angle, 90°.
All the edges have the same length.
A cube also has 8 vertices and 12 edges.
Edges
An edge is a line segment where the two surfaces of a cube meet.
There are twelve edges in a cube, where three edges meet at each vertex.
All edges have equal length and form right angles with the adjacent edges and faces.
Vertices
A vertex is a point where the three edges meet. Vertices is the plural of vertex.
Cube has eight vertices.
Diagonals
The cube has four space diagonals that connect opposite vertices, each of which has a length of √3 times the length of an edge.
Symmetry
Cubes exhibit high symmetry.
They have rotational symmetry of order 4, meaning that you can rotate them by 90 degrees about their centre and they will look the same.
Features of a Cube
It is a three-dimensional, square-shaped figure.
It has 6 faces, 12 edges, and 8 vertices.
All 6 faces are squares with equal area.
All sides have the same length.
Each vertex meets three faces and three edges.
The edges run parallel to those parallel to it.
All angles of a cube are right angles.
Mensuration of Cube
Surface Area of a Cube
The total surface area of a cube is defined as the area of its outer surface.
Derivation of Total Surface Area of a Cube
Since the total surface area of a cube is the area of its outer surface.
total surface area of a cube = 6 ✕ area of one face.
We know that the cube has six square faces and each of the square faces is of the same size, the total surface area of a cube = 6 ✕ area of one face.
Let the length of each edge is “s”.
Area of one square face = length of edge ✕ length of edge
Area of one square face == s ✕ s = s²
Therefore, the total surface area of the cube = 6s²
The total surface area of the cube will be equal to the sum of all six faces of the cube.
The Lateral Surface Area of a Cube.
Imagine yourself sitting in a cube shaped room. You can then see the four walls around you. This denotes the lateral surface area of that room.
That is, the lateral surface area of a cube shaped room is the area of its four walls, excluding the ceiling and the floor.
The lateral surface area of the cube is the sum of areas of its square faces, excluding the area of the top and the bottom face.
So the lateral surface area of a cube = sum of areas of 4 faces = 4a²
The Volume of a Cube
Volume
The volume of a three-dimensional object can be defined as the space required for it.
Similarly, Volume of a cube is defined as the space required for the cube or the Space occupied by the cube.
The volume of a cube can be calculated using the formula V = s3, where “s” represents the length of one side of the cube.
This formula shows that the volume of a cube is directly proportional to the cube of its side length.
The volume is calculated by multiplying the object’s length, breadth, and height. In the case of a cube shape, the length, width, and height are all of the same length. Let us refer to it as “s”.
Hence the volume of the cube is s ✕ s ✕ s = s³
Cubes in Our Daily Life
We encounter many cubes in our daily life such as Ice cubes, sugar cubes, dice and the building blocks used in games.
Cubes play a fundamental role in the study of geometry and serve as a basis for understanding three-dimensional space and concepts such as volume and surface area.
Also, Cubes have many applications in mathematics, engineering, architecture and art etc.
Study Tools
Audio, Visual & Digital Content
Cylinder is an important topic in Mathematics. It is a three-dimensional solid shape that has two parallel circular bases connected by a curved surface.
In this post, we will explore the properties of a cylinder and how to calculate its volume and surface area.
Let’s start with the basic definition of a right circular cylinder.
A cylinder is a solid shape that has two parallel circular bases of equal size and shape.
The curved surface that connects the two bases is called the lateral surface.
The axis of the cylinder is a line passing through the center of both bases.
Types Of Cylinders
(i). Solid Cylinder
(ii). Hollow Cylinder
Area Of A Solid Cylinder
Total Surface Area of Right Circular Cylinder = Curved Surface Area + Cicular Base Area + Circular Top Surface Area.
Since the Cicular Base Area And The Circular Top Surface Area of a cylinder are equal
Total Surface Area of Right Circular Cylinder = Curved Surface Area + 2(Cicular Top Surface Area)
Or
Total Surface Area of Right Circular Cylinder = Curved Surface Area + 2(Cicular Base Surface Area)
Therefore the formula to calculate the surface area of a cylinder is expressed as the following:
$$SA = 2\pi r h + 2\pi r^2$$
where SA is the surface area, r is the radius of the base, and h is the height of the cylinder.
Here, Curved Surface Area, $$CSA = 2\pi r h$$ and
Cicular Base Area = Top Surface Area = $$\pi r^2$$
Volume Of A Solid Cylinder
The formula to calculate the volume of a cylinder is given by:
$$V = \pi r^2 h$$
where V is the volume, r is the radius of the base, and h is the height of the cylinder.
Now let’s take an example to understand how to use these formulas. Suppose we have a cylinder with a radius of 4 cm and a height of 10 cm. To calculate its volume, we can use the formula:
$$V = \pi (4)^2 (10) = 160\pi$$
Therefore, the volume of the cylinder is 160π cubic cm.
To calculate its surface area, we can use the formula:
$$SA = 2\pi (4) (10) + 2\pi (4)^2 = 120\pi$$
Therefore, the surface area of the cylinder is 120π square cm.
In conclusion, understanding the properties of a cylinder and how to calculate its volume and surface area is important in CBSE Class 10 Mathematics. By using the formulas mentioned above, you can easily solve problems related to cylinders.
Hollow Cylinder
A hollow cylinder is a three-dimensional object with a circular base and a cylindrical shape. It is also known as a cylindrical shell. The cylinder has two circular faces and a curved surface. The thickness of the cylinder is uniform and it is hollow from inside.
Volume Of A Hollow Cylinder
The volume of a hollow cylinder can be calculated using the formula V = πh(R2-r2), where h is the height of the cylinder, R is the radius of the outer circle, and r is the radius of the inner circle.
Surface Area Of A Hollow Cylinder
The surface area of a hollow cylinder can be calculated using the formula A = 2πh(R+r), where h is the height of the cylinder, R is the radius of the outer circle, and r is the radius of the inner circle.
Hollow cylinders are used in various applications such as pipes, drums, and containers. They are also used in engineering structures such as bridges and towers.
In conclusion, a hollow cylinder is a useful shape in various fields and can be easily calculated using mathematical equations.
Cone
A cone is a three-dimensional geometric shape that has a circular base and a single vertex. It can be visualized as a pyramid with a circular base. In this note, we will cover the basic concepts and formulas related to cones.
Surface Area of a Cone
The surface area of a cone is the sum of the areas of its base and lateral surface. The formula to calculate the surface area of a cone is:
$$A = \pi r (r + l)$$
Where:
- ( A ) is the surface area of the cone
- $$\pi = 3.14159$$
- ( r ) is the radius of the base of the cone
- ( l ) is the slant height of the cone
Volume of a Cone
The volume of a cone is the amount of space enclosed by it. The formula to calculate the volume of a cone is:
$$V = \frac{1}{3} \pi r^2 h$$
Where:
- ( V ) is the volume of the cone
- ( \pi ) is a mathematical constant approximately equal to 3.14159
- ( r ) is the radius of the base of the cone
- ( h ) is the height of the cone
Example Equations
Here are a few example equations related to cones:
- Equation for calculating the slant height of a cone: $$l = \sqrt{r^2 + h^2}$$
- Equation for calculating the radius of a cone given its slant height and height: $$r = \sqrt{l^2 – h^2}$$
- Equation for calculating the height of a cone given its volume and radius: $$h = \frac{3V}{\pi r^2}$$
Sphere
Solid Sphere
Introduction – A solid sphere is a three-dimensional geometric figure in which all points inside the sphere are at the same distance from its center. – It is a type of 3D shape known as a “sphere” with a uniform density throughout.
Characteristics – The solid sphere has a well-defined volume, surface area, and mass. – It is completely filled with matter.
Volume of Solid Sphere The formula to calculate the volume (\(V_s\)) of a solid sphere is given by: \[ V_s = \frac{4}{3} \pi r^3 \] Where: \(V_s\) = Volume of the solid sphere, \(\pi\) (\(\pi\)) ≈ 3.14159, \(r\) = Radius of the sphere.
Surface Area of Solid Sphere The formula to calculate the surface area (\(A_s\)) of a solid sphere is given by: \[ A_s = 4 \pi r^2 \]
Where: \(A_s\) = Surface area of the solid sphere, \(\pi\) (\(\pi\)) ≈ 3.14159, \(r\) = Radius of the sphere
Mass of Solid Sphere The mass (\(m_s\)) of a solid sphere can be calculated using the formula: \[ m_s = \text{Density} \times V_s \] Where: \(m_s\) = Mass of the solid sphere, \(\text{Density}\) = Density of the material making up the sphere (usually in \(kg/m^3\)), \(V_s\) = Volume of the solid sphere (calculated using the previous formula)
Hollow Sphere
Introduction – A hollow sphere is also a three-dimensional geometric figure, but unlike a solid sphere, it has an empty space inside. – It consists of an outer shell or surface with a certain thickness and an inner empty region.
Characteristics – The hollow sphere has a well-defined outer radius (\(R\)), inner radius (\(r\)), volume, surface area, and mass. – It is partially filled with matter, mainly in the form of the outer shell.
Volume of Hollow Sphere The formula to calculate the volume (\(V_h\)) of a hollow sphere is given by: \[ V_h = \frac{4}{3} \pi (R^3 – r^3) \] Where: – \(V_h\) = Volume of the hollow sphere, \(\pi\) (\(\pi\)) ≈ 3.14159, \(R\) = Outer radius of the sphere, \(r\) = Inner radius of the sphere
Surface Area of Hollow Sphere The formula to calculate the surface area (\(A_h\)) of a hollow sphere is given by: \[ A_h = 4 \pi (R^2 – r^2) \] Where: \(A_h\) = Surface area of the hollow sphere, \(\pi\) (\(\pi\)) ≈ 3.14159, \(R\) = Outer radius of the sphere, \(r\) = Inner radius of the sphere
Mass of Hollow Sphere The mass (\(m_h\)) of a hollow sphere can be calculated using the formula: \[ m_h = \text{Density} \times V_h \] Where: \(m_h\) = Mass of the hollow sphere, \(\text{Density}\) = Density of the material making up the sphere (usually in \(kg/m^3\)), \(V_h\) = Volume of the hollow sphere (calculated using the previous formula)
Hindi Version Dig Deep
Topic Level Resources
Sub – Topics
Select A Topic
Topic:
Chapters Index
Select Another Chapter
Assessments
Personalised Assessments

Statistics | Material
Pre-Requisires
Test & Enrich
English Version Speed Notes
Notes For Quick Recap
Study Tools
Audio, Visual & Digital Content
Hindi Version Dig Deep
Topic Level Resources
Sub – Topics
Select A Topic
Topic:
Chapters Index
Select Another Chapter
Assessments
Personalised Assessments

Probability | Material
Pre-Requisires
Test & Enrich
English Version Probability | Speed Notes
Notes For Quick Recap
Study Tools
Audio, Visual & Digital Content
Probability:
Probability is a measure of uncertainity (an event may happen or may not happen).
Probability is classified into the following two types.
(i) Empirical probability
(ii) theoretical probability.
Empirical Probability Or Experimental Probability
Theoretical probability Or Classical Probability:
Theoretical probability Or Classical Probability is the probability of events based on the results obtained from theoretical approach.
Theoretical Approach
Here, we try to predict the outcomes without performing an actual experiment.
We assume that the outcomes of an experiment are equally likely.
We find that the experimental probability of an event approaches its theoretical probability if the number of trials of an experiment is very large.
Key Terms
Experiment:
Experiment is An activity that causes some well defined outcomes.
Random Experiment
Random experiment is an experiment that
may not give the same result on repitition
under identical conditions,
Trial: Each repition of the activity is called A Trial.
Outcome
Each possible result of a random experiment or a Trial is called its outcome.
Sample Space
The collection of all possible outcomes in a random experiment is called Sample space.
Or
The total number of possible outcomes of a random experiment.
As the number of trials in an experiment increases we may expect the empirical and theoretical probabilities to be nearly the same.
Event:
Any subset of smaple space is called an Event.
Types of Events
Compound Event An event connected to a random experiment is a compound event if it is obtained by combining two or more elementary events connected to the random experiment.
Occurrence of an event An event corresponding to a random experiment is said to occur if any one of the elementary events corresponding to the event is the outcome.
Impossible Events The event which never occurs is an impossible event.
So the probability ofan impossible eventis always zero.
Sure Event The event which certainly occurs is a sure event.In general, it is truethat for anevent E, ( ̅) ( ) Here theevent E is representing “not E”. This is called the compound ofthe event ‘E’.So ‘E’ and E are complementary events.
Theoretical Probability of An Event:
If there are n events associated with a random experiment and m of them are favorable to an event E, then the probability of the event E is denoted by P(E) and is calculated using the follwoing formula.
i.e.,
- Probability of an event E lies between 0 and 1.
- If P (E) =1, then event E is called a certain event or sure event.
- If P (E) =0, then E is called an impossible event.
- Number of non-occurrence of event E = n – m
Where the event
representing non-occurrence of event E, is called the complement of the event E.
Hence, E and
are complementary events.
Sum of the probabilities of all the elementary events of an experiment is
i.e.,
P (E1) + P (E2) + P (E3) … + P (En) = 1
Playing Cards:
A pack of cards consists of four suits. They are
Each suit consists of 13 cards, nine cards numbered 2, 3, 4 ….10, an Ace (B) a Jack (J), a Queen (Q), and a King (K).
Spades and Clubs are black in colour.
Hearts and Diamonds are red in colour.
So there are 26 black cards and 26 red cards.
King, queen and jack are called face cards.
There are totally 12 (4 x3) face cardsin a packof 52 cards.
I.e. in eachsuit we have3 face cards.
Coins:
A coin has two sides namely head and tail.
In the experiment of tossing a coin for once, there are 2 possible outcomes. They are 1 head, 1 tail.
P (Head) = 1/2 = P (Tail)
Dice:
A die is a well-balanced cubewith six facesnumbered from 1 to 6.
Dice is the pluralform. There are six equally likely outcomes 1, 2,3, 4, 5,6 in a single throw. Geometric Probability:
If the total number of outcomes of a trial in a random experiment is infinite, then the above definition is not sufficient to find the probability of an event.
In such cases, the definition of probability is modified and probability so obtained is called Geometric Probability.
The geometric probability p of an event is given by
Hindi Version Dig Deep
Topic Level Resources
Sub – Topics
Select A Topic
Topic:
Chapters Index
Select Another Chapter
Assessments
Personalised Assessments