Pre-Requisires
Test & Enrich
Some Applications Of Trigonometry | Speed Notes
Notes For Quick Recap
Introduction :
One of the main applications of trigonometry is to find the distance between two or more than two places or to find the height of the object or the angle subtended by any object at a given point without actually measuring the distance or heights or angles.
Study Tools
Audio, Visual & Digital Content
Trigonometry is useful to astronomers, navigators, architects and surveyors etc. in solving problems related to heights and distances.
The directions of the objects can be described by measuring :
(i) angle of elevation and (ii) angle of depression
Angles of elevation or angles of depression of the objects are measured by an instrument called The odolite.
The odolite is based on the principles of trigonometry, which is used for measuring angles with a rotating telescope.
In 1856, Sir George Everest first used the giant theodolite, which is now on display in the Museum of the survey of India in Dehradun.
Angle of Elevation:
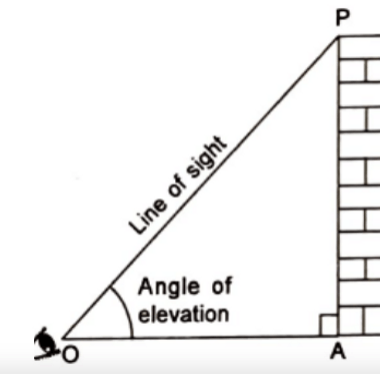
Let P be the position of the object above the horizontal line OA and O be the eye of the observer, then angle AOP is called angle of elevation. It is called the angle of elevation, because the observer has to elevate (raise) his line of sight from the horizontal OA to see the object P. [ When the eye turns upwards above the horizontal line.]
Angle of Depression:
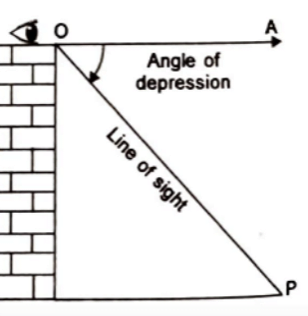
Let P be the position of the object below the horizontal line OA and O be the eye of the observer, then angle AOP is called angle of depression.
It is called the angle of depression because the observer has to depress (lower) his line of sight from the horizontal OA to see the object P.
[When the eye turns downwards below the horizontal line].
Dig Deep
Topic Level Resources
Sub – Topics
Select A Topic
Topic:
Chapters Index
Select Another Chapter
Assessments
Personalised Assessments



Leave a Reply
You must be logged in to post a comment.