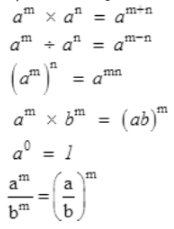Data Handling | Study
Assess
Interact
Pre-Requisires
Test & Enrich
Pre – Requisite

English Version
Data Handling | Speed Notes
Notes For Quick Recap
The collection, recording and presentation of data help us organiseour experiences and draw inferences from them.
Before collecting data we need to know what we would use it for.
The data that is collected needs to be organised in a propertable, so that it becomeseasy to understand and interpret. (Scroll down to continue …).
Study Tools
Audio, Visual & Digital Content
Average is a numberthat represents or shows the central tendencyof a group of observations or data.
Arithmetic mean is one of the representative values of data.
Mean = sum of all observations/ Number of observations.
Mode is another form of central tendency or representative value.
The mode of a set of observations is the observation that occurs most often.
If each of the value in a data is occurring one time, then all are mode.
Sometimes we also say that this data has no mode since none of them is occurring frequently.
Median is also a form of representative value.
It refers to the value which lies in the middle of the data with half of the observations above it and the other half below it.
.
A bar graph is a representation of numbers using bars of uniform widths.
Double bar graphshelp to comparetwo collections of data at a glance.
Double bar graphshelp to comparetwo collections of data at a glance.
There are situations in our life, that are certain to happen, some that are impossible and some that may or may not happen.
The situation that may or may not happen has a chanceof happening.
Probability: A branch of mathematics that is capable of calculating the chance or likelihood of an event taking place (in percentage terms).
If you have 10 likelihoods and you want to calculate the probability of 1 event taking place,it is said that its probability is 1/10 or event has a 10% probability of taking place.
Events that have many possibilities can have probability between 0 and 1.
Important Formulae – Data Handling
1. A trial is anaction which results in one or several outcomes. 2. An experiment in whichthe result ofa trial cannot be predicted inadvance is called a random experiment.
3. An event associated to a random experiment is thecollection of someoutcomes of theexperiment.
4. An event associated witha random experiment is said tohappen if anyone of theoutcomes satisfying thedefinition of theevent is anoutcome of theexperiment when it is performed.
5. The Empirical probability ofhappening of an event E is defined as: P(E)= Number of trials in which the event happened/ Total number of trials.

Hindi Version
Dig Deep
Topic Level Resources
Sub – Topics
Select A Topic
Topic:
Chapters Index
Select Another Chapter
Assessments
Personalised Assessments
Assess
November 5, 2023
Simple Equations | Study
Assess
Interact
Pre-Requisires
Test & Enrich
Pre – Requisite

English Version
Simple Equations | Speed Notes
Notes For Quick Recap
An equation isa condition ona variable suchthat two expressions in the variable should have equalvalue.
Thevalue of thevariable for whichthe equation issatisfied is called the solution ofthe equation.
An equation remains the same if the LHSand the RHSare interchanged. (Scroll down to continue …)
Study Tools
Audio, Visual & Digital Content
In case ofthe balanced equation, if we add the same number to both thesides, or subtract the same number from both the sides,
or
multiply both sidesby the same number, or divide both sidesby the samenumber, the balance remains un disturbed,
i.e.,the value of the LHS remains equal to the value of the RHS The above property gives a systematic method of solving an equation.
We carry out a series of identical mathematical operations on the two sides of the equation in such a waythat on oneof the sides we get justthe variable. Thelast step isthe solution of the equation.
Transposing means moving to the other side.
Transposition of a number has the same effect as adding same number to (or subtracting the same number from) both sides of the equation.
Whenyou transpose a number fromone side ofthe equation tothe other side, you change itssign.
For example, transposing +3 fromthe LHS tothe RHS in equation x + 3 = 8 gives x = 8 – 3 (= 5).
We can carry out the transposition of an expression in thesame way as the transposition of a number.
We havelearnt how to construct simple algebraic expressions corresponding to practical situations.
Wealso learnt how,using the technique of doing thesame mathematical operation (for example adding the samenumber) on bothsides, we could build an equation starting fromits solution.
Further, we also learnt that we could relate a given equation tosome appropriate problem/puzzlefrom the equation. practical situation and build a practical word.

Hindi Version
Dig Deep
Topic Level Resources
Sub – Topics
Select A Topic
Topic:
Chapters Index
Select Another Chapter
Assessments
Personalised Assessments
Assess
November 5, 2023
Lines and Angles | Study
Assess
Interact
Pre-Requisires
Test & Enrich
Pre – Requisite

English Version
Speed Notes
Notes For Quick Recap
We recall that
(i) A line-segment has two end points.
(ii) A ray has only one end point (its vertex);and
(III) A line has no end points on either side.
An angle is formed when two lines (or rays or line-segments) meet.
Study Tools
Audio, Visual & Digital Content
Important Formulas | Lines and Angles
When two lines l and m meet, we say they intersect; the meeting point is calledthe point of intersection.
When lines drawnon a sheet of paper do not meet, howeverfar produced, we call them to be parallel lines.
Point: A point name a location.
Line: A line is perfectlystraight and extends forever in both direction.
Line segment: A line segmentis the part of a line betweentwo points.
Ray: A ray is part of a line that starts at one point and extendsforever in one direction.
Intersecting lines: Two or more lines that have one and only one point in common.
The common point where all the intersecting lines meet is called the point of
intersection.
Transversal: A line intersects two or more lines that lie in the same plane in distinct points.
Parallel lines: Two lineson a plane that nevermeet. They distance apart.
Complementary Angles: Two angles whose measures add to 90^O Supplementary Angles: Two angles whose measures add to 180 ^o
Adjacent Angles: Two angles have a common vertex and a
common interiorpoints.
Linear pairs: A pair of adjacentangles whose non-common sides are oppositerays. Vertically Opposite Angles: Two angles formed by two intersecting lines have common arm.
Angles made by Transversal: When two lines are intersecting by a transversal, eight anglesare formed.
Transversal of Parallel Lines: If two parallel lines are intersected by a transversal, each pair of:
Corresponding angles are congruent. Alternateinterior angles are congruent. Alternateexterior angles are congruent.
If the transversal is perpendicular to the parallellines, all of the angles formed are congruent to 90 o angles.
1. A linewhich intersects two or more given lines at distinct points is called a transversal to the given lines.
2. Lines in a plane areparallel if theydo not intersect when produced indefinitely in either direction.
3. The distance between two intersecting lines is zero.
4. The distance between two parallel lines is thesame everywhere andis equal tothe perpendicular distance between them.
5. If two parallel lines are intersected by a transversal then (i) pairs ofalternate (interior orexterior) angles are equal. (ii) pairs of corresponding angles are equal. (iii) interior angles onthe same sideof the transversal are supplementary. 6. If twonon-parallel lines areintersected by transversal then none of (i), (ii) and (iii) hold true in 5. 7. If twolines are intersected by a transversal, thenthey are parallel ifany one of thefollowing is true: (i) The angles of a pair of corresponding angles are equal. (ii) The angles of a pairof alternate interior angles are equal. (iii) The angles of a pairof interior angles on the sameside of the transversal are supplementary.

Hindi Version
Dig Deep
Topic Level Resources
Sub – Topics
Select A Topic
Topic:
Chapters Index
Select Another Chapter
Assessments
Personalised Assessments
Assess
November 5, 2023

Understanding Quadrilaterals | Study

Assess

Interact

Pre-Requisires

Test & Enrich

Pre – Requisite

https://www.youtube.com/watch?v=5Wi9JTYOblw&list=PLEuUy4TjqFeAD5Xcp85qBGE8VHxrYIu7F&pp=gAQBiAQB

English Version

Speed Notes

Notes For Quick Recap

A quadrilateral has 10 parts – 4 sides, 4 angles and 2 diagonals. Five measurements can determine a quadrilateral uniquely. (Scroll down to continue …)

Study Tools

Audio, Visual & Digital Content

Curve: Curve is a figure formed on a plane surface by joining a number of non linear points without lifting a pencil.

Open Curve: An open curve is a curve which does not end at the same starting point or which does not intersect itself.

Closed Curve: Closed curve is a curve which intersects itself or which starts and ends at the same point.

Simple Closed Curve: A simple closed curve is a closed curve that does not intersect itself.

Polygon: Polygon is a closed figure bounded by three or more line segments such that each line segment intersects the other two line segements at exactly two other points (vertices) as shown in the following figures.

Polygons are classified into two types on the basis of interior angles: as (i) Convex polygon (ii) Concave polygon

(a) Convex Polygon: In this case, each angle is either acute or obtuse (angle < 180 ^o) as shown in the following figures.

Concave Polygon: In this case, any one angle is reflex (angle > 180°) and one diagonal is outside the polygon as shown in the following figures.

On the basis of sides, there are two types of polygons :

(a) Regular Polygon: A convex polygon is called a regular polygon, if all its sides and angles are equal as shown in the following figures.

Each angle of a regular polygon of n-sides =

Important results on polygon :

For a regular polygon of n sides (n > 2).

(b) Irregular Polygon: A polygon in which all the sides are unequal as shown in the following figures,

Triangle :

A simple closed figure bounded by three line segments is called a triangle, it has three sides as AB, BC and AC; three vertices as A, B and C and three interior angles A, ZB and ZCand the sum of all angles is 180°.

i.e., <A + <B + <C = 180°

Quadrilateral:

A simple closed figure bounded by four line segments is called a quadrilateral, it has four sides i.e.,

AB, BC, CD and AD and four vertices as A, B, Can d D and the sum of all angles of a quadrilateral is 360.

Practical Geometry

Five measurements can determine a quadrilateral uniquely.

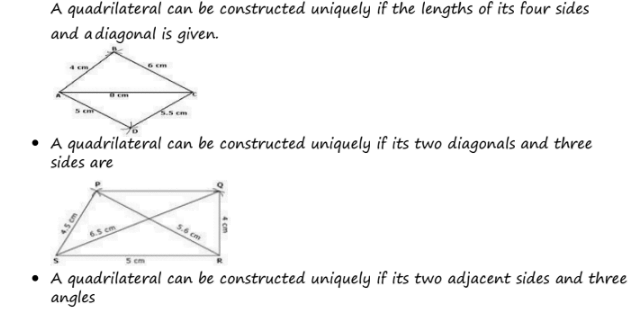
A quadrilateral can be constructed uniquely if the lengths of its four sides and a diagonal is given.

A quadrilateral can be constructed uniquely if its two diagonals and three sides are

known.

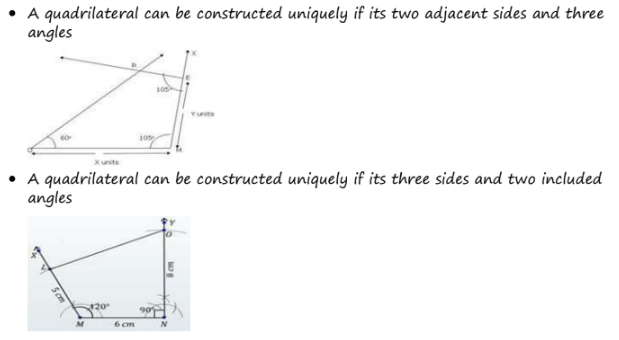
A quadrilateral can be constructed uniquely if its two adjacent sides and three angles

are known.

A quadrilateral can be constructed uniquely if its three sides and two included angles

are given.

Quadrilateral

Quadrilateral is a closed figure with four sides.

Characteristics of a quadrilateral

Angle Sum Property of a Quadrilateral:

Qudrilateral is a four sided closed figure.

Sum of all angles of a quadrilateral is 360°.

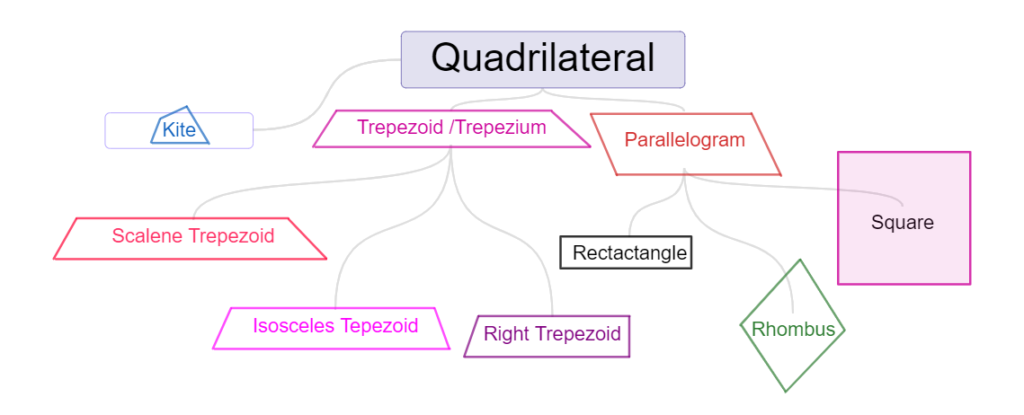
Types Of Quadrilaterals

Quadrilaterals are broadly classified into three categories as:

(i) Kite

(ii) Trapezium

(ii) Parallelogram

Kite:

Kite

(i) Kite has no parallel sides

(ii) Kite has a pair of equal adjacent sides.

(ii) It is not a parallelogram

Characteristics Of Kite:

Perimeter Of Square

Area Of Kite

Trapezium:

Trapezium is a quadrilateral with the following characteristics:

(i) One pair of opposite sides is parallel to each other.

(ii) The other pair of opposite sides may not be parallel to each other.

Characteristics Of Trapezium

(i) Sum of all angles of a quadrilateral is 360°.

(ii) One pair of opposite sides is parallel to each other.

(iii) The other pair of opposite sides need not be parallel to each other.

Types Of Trapezium:

Quadrilaterals are broadly classified into two categories as:

(i) Isosceles Trapezium.

(ii) Scalene Trapezium.

(i) Right Trapezium.

Isosceles Trapezium:

Isosceles Trapezium is a quadrilateral with the following characteristics:

(i) One pair of opposite sides is parallel to each other.

(ii) The other pair of opposite sides are equal.

(iii) The other pair of opposite sides need not be parallel to each other.

Isosceles Trapezium is a trapezium with the following characteristics:

(i) One pair of opposite sides is parallel to each other.

(ii) The other pair of opposite sides are equal.

(iii) The other pair of opposite sides need not be parallel to each other.

Characteristics Of Isosceles Trapezium

(i) Sum of all angles of a quadrilateral is 360°.

(ii) One pair of opposite sides is parallel to each other.

(iii) The other pair of opposite sides are equal.

(iv) The other pair of opposite sides need not be parallel to each other.

Scalene Trapezium:

Scalene trapezium: Classified by the length of the legs or the measurement of their angles.

Characteristics Of Scalene Trapezium

Right Trapezium:

Right trapezium: Has one pair of parallel sides and one pair of right angles.

Characteristics Of Right Trapezium

Perimeter Of Trapezium

Area Of Trapezium

Parallelogram:

Parallelogram is a quadrilateral with the following characteristics:

(i) Two pairs of opposite sides are parallel to each other.

(ii) Two pairs of opposite sides are equal in length.

Characteristics of a parallelogram

(i) Sum of all angles of a Parallelogram is 360°.

(ii) Two pairs of opposite sides are parallel to each other.

(ii) Two pairs of opposite sides are equal in length.

(ii) Two pairs of opposite angles are equal.

(iii) Diagonals bisect each other.

(iv) Diagonals need not be equal to each other.

(v) Diagonals divide it into two congruent triangles.

Types Of Parallelogram

Parallelograms are broadly classified into three categories as:

(i) Rectangle

(ii) Rhombus

(iii) Square

Perimeter Of Parallelogram

Area Of Parallelogram

Rectangle:

Rectangle is a quadrilateral with the following characteristics:

(i) Two pairs of opposite sides are parallel to each other.

(ii) Two pairs of opposite sides are equal in length.

(iii) All four angles are right angles. (each angle is 90 ^o).

Characteristics Of Rectangle

(i) Sum of all angles of a quadrilateral is 360°.

(ii) Two pairs of opposite sides are parallel to each other.

(ii) Two pairs of opposite sides are equal in length.

(iii) All four angles are right angles. (each angle is 90 ^o).

(iii) Diagonals bisect each other.

(iv) Diagonals are equal to each other.

(v) Diagonals of a rectangle divide it into two congruent triangles.

Conclusions:

Every Rectangle is a Parallelogram. But Every Parallelogram need not to be a Rectangle.

Condition for a rhombus to be a square:

If all four angles of a parallelogram are right angles. (each angle is 90 ^o), the parallelogram becomes a Rectangle.

Perimeter Of Rectangle

Area Of Recatangle

Rhombus:

Rhombus is a quadrilateral with the following characteristics:

(i) Two pairs of opposite sides are parallel to each other.

(ii) All four sides are equal in length.

Characteristics Of Rhombus

(i) Sum of all angles of a quadrilateral is 360°.

(ii) Two pairs of opposite sides are parallel to each other.

(ii) All four sides are equal in length.

(ii) Two pairs of opposite angles are equal.

(iii) Diagonals bisect each other.

(iv) Diagonals need not be equal to each other.

(v) Diagonals divide a Rhombus into two congruent triangles.

Conclusions:

Every Rhombus is a Parallelogram. But Every Parallelogram need not to be a Rhombus.

Condition for a rhombus to be a square:

If all the sides of a parallelogram are equal, the parallelogram becomes a Rhombus.

Perimeter Of Rhombus

Area Of Rhombus

Square:

Square is a quadrilateral with the following characteristics:

(i) Two pairs of opposite sides are parallel to each other.

(ii) All four sides are equal in length.

(iii) All four angles are right angles. (each angle is 90 ^o).

Characteristics Of Square

(i) Sum of all angles of a quadrilateral is 360°.

(ii) Two pairs of opposite sides are parallel to each other.

(iii) All four sides are equal in length.

(iv) All four angles are right angles. (each angle is 90 ^o).

(v) Diagonals bisect each other.

(vi) Diagonals need not be equal to each other.

(vii) Diagonals divide a Rhombus into two congruent triangles.

Conclusions:

Every square is a Rhombus. But Every Rhombus need not to be a square.

Condition for a rhombus to be a square:

If all the angles of a rhombus are right angles (euqal to 90^o), the rhombus becomes a square.

2. Every Square is a prallelogram. But Every prallelogram need not to be a square.

Condition for a prallelogram to be a square:

(i) If all the angles of a parallelogram are right angles (euqal to 90^o), and all the sides of a parallelogram are equal in length, the parallelogram becomes a square.

3. Every Square is a rectangle. But Every Rectangle need not to be a square.

Condition for a Rectangle to be a square:

If all the sides of a Rectangle are equal in length, the Rectangle becomes a square.

If all the sides of a parallelogram are equal, the parallelogram becomes a Rhombus.

Perimeter Of Square

Area Of Square

Important Points To Remember

The diagonals of a parallelogram are equal if and only if it is a rectangle.
If a diagonal of a parallelogram bisects one of the angles of the parallelogram then it also bisects the opposite angle.
In a parallelogram, the bisectors of any two consecutive angles intersect at a right angle.
The angle bisectors of a parallelogram form a rectangle.

Mid Point Theorem

A line segment joining the mid points of any two sides of a triangle is parallel to the third side and length of the line segment is half of the parallel side.

Converse Of Mid Point Theorem

A line through the midpoint of a side of a triangle parallel to another side bisects the third side.

Intercept Theorem

If there are three parallel lines and the intercepts made by them on one transversal are equal then the intercepts on any other transversal are also equal.

svg+xml;nitro-empty-id=ODUyOjUzOA==-1;base64,PHN2ZyB2aWV3Qm94PSIwIDAgMSAxIiB3aWR0aD0iMSIgaGVpZ2h0PSIxIiB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciPjwvc3ZnPg==

Angle Sum Property of a Quadrilateral

The sum of the four angles of a quadrilateral is 360°

If we draw a diagonal in the quadrilateral, it divides it into two triangles.

And we know the angle sum property of a triangle i.e. the sum of all the three angles of a triangle is 180°.

The sum of angles of ∆ADC = 180°.

The sum of angles of ∆ABC = 180°.

By adding both we get ∠A + ∠B + ∠C + ∠D = 360°

Hence, the sum of the four angles of a quadrilateral is 360°.

Example

Find ∠A and ∠D, if BC∥ AD and ∠B = 52° and ∠C = 60° in the quadrilateral ABCD.

Solution:

Given BC ∥ AD, so ∠A and ∠B are consecutive interior angles.

So ∠A + ∠B = 180° (Sum of consecutive interior angles is 180°).

∠B = 52°

∠A = 180°- 52° = 128°

∠A + ∠B + ∠C + ∠D = 360° (Sum of the four angles of a quadrilateral is 360°).

∠C = 60°

128° + 52° + 60° + ∠D = 360°

∠D = 120°

∴ ∠A = 128° and ∠D = 120 °.

Types of Quadrilaterals

Remark: A square, Rectangle and Rhombus are also a parallelogram.

Properties of a Parallelogram

Theorem 1: When we divide a parallelogram into two parts diagonally then it divides it into two congruent triangles.

∆ABD ≅ ∆CDB

Theorem 2: In a parallelogram, opposite sides will always be equal.

Theorem 3: A quadrilateral will be a parallelogram if each pair of its opposite sides will be equal.

Here, AD = BC and AB = DC

Then ABCD is a parallelogram.

Theorem 4: In a parallelogram, opposite angles are equal.

In ABCD, ∠A = ∠C and ∠B = ∠D

Theorem 5: In a quadrilateral, if each pair of opposite angles is equal, then it is said to be a parallelogram. This is the reverse of Theorem 4.

Theorem 6: The diagonals of a parallelogram bisect each other.

Here, AC and BD are the diagonals of the parallelogram ABCD.

So the bisect each other at the centre.

DE = EB and AE = EC

Theorem 7: When the diagonals of the given quadrilateral bisect each other, then it is a parallelogram.

This is the reverse of the theorem 6.

The Mid-point Theorem

1. If a line segment joins the midpoints of the two sides of the triangle then it will be parallel to the third side of the triangle.

If AB = BC and CD = DE then BD ∥ AE.

2. If a line starts from the midpoint of one line and that line is parallel to the third line then it will intersect the midpoint of the third line.

If D is the midpoint of AB and DE∥ BC then E is the midpoint of AC.

Example

Prove that C is the midpoint of BF if ABFE is a trapezium and AB ∥ EF.D is the midpoint of AE and EF∥ DC.

Solution:

Let BE cut DC at a point G.

Now in ∆AEB, D is the midpoint of AE and DG ∥ AB.

By midpoint theorem, G is the midpoint of EB.

Again in ∆BEF, G is the midpoint of BE and GC∥ EF.

So, by midpoint theorem C is the midpoint of BF.

Hence proved.

Hindi Version

Dig Deep

Topic Level Resources

Sub – Topics

Select A Topic

Topic:

Chapters Index

Select Another Chapter

Assessments

Personalised Assessments

Assess

November 5, 2023

CBSE 8 | Mathematics – Study – Premium
Educational Tools | Full Course
Study Tools
Audio, Visual & Digital Content
Assessment Tools
Assign, Assess & Analyse
November 5, 2023
Direct And Inverse Proportions | Study
Assess
Interact
Pre-Requisires
Test & Enrich
Pre – Requisite

English Version
Direct and Inverse Proportions | Speed Notes
Notes For Quick Recap
Variations: If the values of two quantities depend on each other in such a way that a change in one causes corresponding change in the other, then the two quantities are said to be in variation. (Scroll down to continue …)
Study Tools
Audio, Visual & Digital Content
Direct Variation or Direct Proportion:
Extra:
Two quantities x and y are said to be in direct proportion if they increase (decrease) together in such a manner that the ratio of their corresponding values remains
constant. That is if
=k [k is a positive number, then x and y are said to vary directly.
In such a case if y₁, y₂are the values of y corresponding to the values x₁, x of x
respectively then = .
If the number of articles purchased increases, the total cost also increases. More than money deposited in a bank, more is the interest earned.
Quantities increasing or decreasing together need not always be in direct proportion, same in the case of inverse proportion.
When two quantities x and y are in direct proportion (or vary directly), they are
written as
. Symbol
stands for ‘is proportion to’.
Inverse Proportion: Two quantities x and y are said to be in inverse proportion if an increase in x causes a proportional decrease in y (and vice-versa) in such a manner that the product of their corresponding values remains constant. That is, if xy
= k, then x and y are said to vary inversely. In this case if y₁, y₂are the values of y
corresponding to the values x₁, x₂of x respectively then
^x1^{, Y}1 = ^x2^{, y}2 or
=
When two quantities x and y are in inverse proportion (or vary inversely), they are
written as x
. Example: If the number of workers increases, time taken to finish
the job decreases. Or If the speed will increase the time required to cover a given distance decreases.

Hindi Version
Dig Deep
Topic Level Resources
Sub – Topics
Select A Topic
Topic:
Chapters Index
Select Another Chapter
Assessments
Personalised Assessments
Assess
November 5, 2023
Factorisation | Study
Assess
Interact
Pre-Requisires
Test & Enrich
Pre – Requisite

English Version
Speed Notes
Notes For Quick Recap
Factorisation: Representation of an algebraic expression as the product of two or more expressions is called factorization. Each such expression is called a factor of the given algebraic expression. (Scroll down to continue …)
Study Tools
Audio, Visual & Digital Content
When we factorise an expression, we write it as a product of factors. These factors may be numbers, algebraic variables or algebraic expressions.
An irreducible factor is a factor which cannot be expressed further as a product of factors.
A systematic way of factorising an expression is the common factor method. It consists of three steps:
Write each term of the expression as a product of irreducible factors
Look for and separate the common factors and
Combine the remaining factors in each term in accordance with the distributive law.
Sometimes, all the terms in a given expression do not have a common factor; but the terms can be grouped in such a way that all the terms in each group have a common factor. When we do this, there emerges a common factor across all the groups leading to the required factorisation of the expression. This is the method of regrouping.
In factorisation by regrouping, we should remember that any regrouping (i.e., rearrangement) of the terms in the given expression may not lead to factorisation. We must observe the expression and come out with the desired regrouping by trial and error.
A number of expressions to be factorised are of the form or can be put into the form: a²+ 2ab + b², a²– 2ab + b², a²– b²and x² + (a + b)x + ab. These expressions can be easily factorised using Identities I, II, III and IV
a²+ 2ab + b²= (a + b)²
a²– 2ab + b²= (a – b)²
a²– b²= (a + b) (a – b)
Factorisation
x² + (a + b)x + ab = (x + a)(x + b)
In expressions which have factors of the type (x + a) (x + b), remember the numerical term gives ab.
Its factors, a and b, should be so chosen that their sum, with signs taken care of, is the coefficient of x.
We know that in the case of numbers, division is the inverse of multiplication. This idea is applicable also to the division of algebraic expressions.
In the case of division of a polynomial by a monomial, we may carry out the division either by dividing each term of the polynomial by the monomial or by the common factor method.
In the case of division of a polynomial by a polynomial, we cannot proceed by dividing each term in the dividend polynomial by the divisor polynomial. Instead, we factorise both the polynomials and cancel their common factors.
In the case of divisions of algebraic expressions that we studied in this chapter, we have Dividend = Divisor × Quotient.
In general, however, the relation is Dividend = Divisor × Quotient + Remainder
Thus, we have considered in the present chapter only those divisions in which the remainder is zero.
There are many errors students commonly make when solving algebra exercises.
You should avoid making such errors.
Hindi Version
Dig Deep
Topic Level Resources
Sub – Topics
Select A Topic
Topic:
Chapters Index
Select Another Chapter
Assessments
Personalised Assessments
Assess
November 5, 2023
Introduction to Graphs | Study
Assess
Interact
Pre-Requisires
Test & Enrich
Pre – Requisite

English Version
Speed Notes
Notes For Quick Recap
Graphical presentation of data is easier to understand.
A bar graph is used to show comparison among categories.
A pie graph is used to compare parts of a whole.
A Histogram is a bar graph that shows data in intervals. (Scrol down to continue …)
Study Tools
Audio, Visual & Digital Content
Introduction to Graphs
A line graph displays data that changes continuously over periods of time. A line graph which is a whole unbroken line is called a linear graph.
For fixing a point on the graph sheet we need, x-coordinate and y-coordinate.
The relation between dependent variable and
through a graph.
independent variable is shown
A Bar Graph: A pictorial representation of numerical data in the form of bars (rectangles) of uniform width with equal spacing. The length (or height) of each bar
represents the given number.
A Pie Graph: A pie graph is used to compare parts of a whole. The various
observations or components are represented by the sectors of the circle.
A Histogram: Histogram is a type of bar diagram, where the class intervals are shown on the horizontal axis and the heights of the bars (rectangles) show the frequency of the class interval, but there is no gap between the bars as there is no gap between the
class intervals.
Linear Graph: A line graph in which all the line segments form a part of a single line. Coordinates: A point in Cartesian plane is represented by an ordered pair of numbers.
Ordered Pair: A pair of numbers written in specified order.
Hindi Version
Dig Deep
Topic Level Resources
Sub – Topics
Select A Topic
Topic:
Chapters Index
Select Another Chapter
Assessments
Personalised Assessments
Assess
November 5, 2023
Exponents And Powers | Study
Assess
Interact
Pre-Requisires
Test & Enrich
Pre – Requisite

English Version
Exponents and Powers | Speed Notes
Notes For Quick Recap
Numbers with exponents obey the following laws of exponents.
Very small numbers can be expressed in standard form using negative exponents. (Scroll down to continue …)
Study Tools
Audio, Visual & Digital Content
Use of Exponents to Express Small Number in Standard form:
Very large and very small numbers can be expressed in standard form.
Standard form is also called scientific notation form.
(iii) A number written as number such that is said to be in standard form if m is a decimal and n is either a positive or a negative integer.
Examples: 150,000,000,000 = 1.5 x 10¹¹.
Exponential notation is a powerful way to express repeated multiplication of the same number.
For any non-zero rational number ‘a’ and a natural number n, the product a x a x a x x a(n times) = aⁿ.
It is known as the nth power of ‘a’ and is read as ‘a’ raised to the power n’.
The rational number a is called the base and n is called exponent.
Hindi Version
Dig Deep
Topic Level Resources
Sub – Topics
Select A Topic
Topic:
Chapters Index
Select Another Chapter
Assessments
Personalised Assessments
Assess
November 5, 2023
Data Handling | Study
Assess
Interact
Pre-Requisires
Test & Enrich
Pre – Requisite

English Version
Data Handling | Speed Notes
Notes For Quick Recap
Data Handling: Deals with the process of collecting data, presenting it and getting result.
Data mostly available to us in an unorganised form is called raw data. (Scroll down to continue …)
Study Tools
Audio, Visual & Digital Content
Grouped data can be presented using histogram. Histogram is a type of bar diagram, where the class intervals are shown on the horizontal axis and the heights of the bars show the frequency of the class interval. Also, there is no gap between the bars as there is no gap between the class intervals.
In order to draw meaningful inferences from any data, we need to organise the data systematically.
Frequency gives the number of times that a particular entry occurs.
Raw data can be ‘grouped’ and presented systematically through ‘grouped frequency distribution’.
Statistics: The science which deals with the collection, presentation, analysis and interpretation of numerical data.
Observation: Each entry (number) in raw data.
Range: The difference between the lowest and the highest observation in a given data.
Array: Arranging raw data in ascending or descending order of magnitude. Data can also presented using circle graph or pie chart. A circle graph shows the relationship between a whole and its part.
There are certain experiments whose outcomes have an equal chance of occurring. A random experiment is one whose outcome cannot be predicted exactly in advance. Outcomes of an experiment are equally likely if each has the same chance of occurring.
Frequency: The number of times a particular observation occurs in the given data.
Class Interval: A group in which the raw data is condensed.
(i) Continuous: The upper limit of a class interval coincides with the lower limit of the next class.

Hindi Version
Dig Deep
Topic Level Resources
Sub – Topics
Select A Topic
Topic:
Chapters Index
Select Another Chapter
Assessments
Personalised Assessments
Assess
November 5, 2023
Squares And Square Roots | Study
Assess
Interact
Pre-Requisires
Test & Enrich
Pre – Requisite

English Version
Squares and Square Roots | Speed Notes
Notes For Quick Recap
Square: Number obtained when a number is multiplied by itself. It is the number raised to the power 2. 2²= 2 x 2=4(square of 2 is 4).
If a natural number m can be expressed as n², where n is also a natural number, then m is a square number. (Scroll down to continue …)
Study Tools
Audio, Visual & Digital Content
All square numbers end with 0, 1, 4, 5, 6 or 9 at unit’s place. Square numbers can only have even number of zeros at the end. Square root is the inverse operation of square.
There are two integral square roots of a perfect square number.
Positive square root of a number is denoted by the symbol For example, 3²=9 gives
Perfect Square or Square number: It is the square of some natural number. If m=n², then m is a perfect square number where m and n are natural numbers. Example: 1=1 x 1=12, 4=2 x 2=2².
Properties of Square number:
A number ending in 2, 3, 7 or 8 is never a perfect square. Example: 152, 1028, 6593 etc.
A number ending in 0, 1, 4, 5, 6 or 9 may not necessarily be a square number. Example: 20, 31, 24, etc.
Square of even numbers are even. Example: 2²= 4, 4²=16 etc.
Square of odd numbers are odd. Example: 5²= 25, 9²= 81, etc.
A number ending in an odd number of zeroes cannot be a perferct square. Example: 10, 1000, 900000, etc.
The difference of squares of two consecutive natural number is equal to their sum. (n + 1)²– n²= n+1+n. Example: 4²– 3²=4 + 3=7. 12²– 11²=12+11 =23, etc.
A triplet (m, n, p) of three natural numbers m, n and p is called Pythagorean
triplet, if m²+ n²= p²: 3²+ 4²= 25 = 5²
Hindi Version
Dig Deep
Topic Level Resources
Sub – Topics
Select A Topic
Topic:
Chapters Index
Select Another Chapter
Assessments
Personalised Assessments
Assess
November 5, 2023
Cubes And Cube Roots | Study
Assess
Interact
Pre-Requisires
Test & Enrich
Pre – Requisite

English Version
Cubes and Cube Root | Speed Notes
Notes For Quick Recap
Cube number: Number obtained when a number is multiplied by itself three times. 2³= 2 x 2 x 2 = 8, 3³= 3 x 3 x 3=27, etc.
Numbers like 1729, 4104, 13832, are known as Hardy – Ramanujan Numbers. They
can be expressed as sum of two cubes in two different ways.
Study Tools
Audio, Visual & Digital Content
Numbers obtained when a number is multiplied by itself three times are known as cube numbers. For example 1, 8, 27, … etc.
If in the prime factorisation of any number each factor appears three times, then the
number is a perfect cube.
The symbol
denotes cube root. For example
Perfect Cube: A natural number is said to be a perfect cube if it is the cube of some natural number. Example: 8 is perfect cube, because there is a natural number 2 such that 8 = 2³, but 18 is not a perfect cube, because there is no natural number whose cube is 18.
The cube of a negative number is always negative.
Properties of Cube of Number:
Cubes of even number are even.
Cubes of odd numbers are odd.
The sum of the cubes of first n natural numbers is equal to the square of their sum.
Cubes of the numbers ending with the digits 0, 1, 4, 5, 6 and 9 end with digits 0, 1, 4, 5, 6 and 9 respectively.
Cube of the number ending in 2 ends in 8 and cube of the number ending in 8 ends in 2.
Cube of the number ending in 3 ends in 7 and cube of the number ending in 7
ends in 3.
Hindi Version
Dig Deep
Topic Level Resources
Sub – Topics
Select A Topic
Topic:
Chapters Index
Select Another Chapter
Assessments
Personalised Assessments
Assess
November 5, 2023
Comparing Quantities | Study
Assess
Interact
Pre-Requisires
Test & Enrich
Pre – Requisite

English Version
Comparing Quantities | Speed Notes
Notes For Quick Recap
Ratio: Comparing by division is called ratio. Quantities written in ratio have the sameunit. Ratio has no unit. (Scroll down to continue …)
Study Tools
Audio, Visual & Digital Content
Equality of two ratios is called proportion. Product of extremes = Product of means
Percentage: Percentage means for every hundred. The result of any division in
whichthe divisor is 100 is a percentage. The divisor is denoted by a special
symbol %, read as percent. Profit and Loss:
(i) Cost Price (CP): The amount for which an article is bought. (ii) Selling Price (SP): The amount for which an article is sold. Additional expenses made after buying an article are included in the cost price
and are known as overhead expenses. These may include expenses like amount
spent onrepairs, labour charges, transportation, etc. Discount is a reduction given on marked price. Discount = Marked Price – Sale
Price. Discount can be calculated when discount percentage is given. Discount
https://www.youtube.com/watch?v=5Wi9JTYOblw&list=PLEuUy4TjqFeAD5Xcp85qBGE8VHxrYIu7F&pp=gAQBiAQB
Hindi Version
Dig Deep
Topic Level Resources
Sub – Topics
Select A Topic
Topic:
Chapters Index
Select Another Chapter
Assessments
Personalised Assessments
Assess
November 5, 2023
Algebraic Expressions And Identities | Study
Assess
Interact
Pre-Requisires
Test & Enrich
Pre – Requisite

English Version
Algebraic Expressions and Identities | Speed Notes
Notes For Quick Recap
Expressions are formed from variables and constants.
Constant: A symbol having a fixed numerical value.
Example: 2,, 2.1, etc. (Scroll down to continue …)
Study Tools
Audio, Visual & Digital Content
Variable: A symbol which takes various numerical values. Example: x, y, z, etc.
Algebric Expression: A combination of constants and variables connected by the sign
+, -, and is called algebraic expression.
Terms are added to form expressions.
Terms themselves are formed as product of factors.
Expressions that contain exactly one, two and three terms are called monomials, binomials and trinomials respectively.
In general, any expression containing one or more terms with non-zero coefficients (and with variables having non- negative exponents) is called a polynomial.
Like terms are formed from the same variables and the powers of these variables are the same, too.
Coefficients of like terms need not be the same.
While adding (or subtracting) polynomials, first look for like terms and add (or subtract) them; then handle the unlike terms.
There are number of situations in which we need to multiply algebraic expressions: for example, in finding area of a rectangle, the sides of which are given as expressions.
Monomial: An expression containing only one term. Example: -3, 4x, 3xy, etc.
Binomial: An expression containing two terms. Example: 2x-3, 4x+3y, xy-4, etc.,
Polynomial: In general, any expression containing one or more terms with non-zero coefficients (and with variables having non-negative exponents).
A polynomial may contain any number of terms, one or more than one.
A monomial multiplied by a monomial always gives a monomial.
Multiplication of a Polynomial and a monomial:
While multiplying a polynomial by a monomial, we multiply every term in the polynomial by the mononomial.
Trinomial: An expression containing three terms.
Example:
3x+2y+5z, etc.
In carrying out the multiplication of a polynomial by a binomial (or trinomial), we multiply term by term, i.e., every term of the polynomial is multiplied by every term in the binomial (or trinomial).
Note that in such multiplication, we may get terms in the product which are like and have to be combined.
An identity is an equality, which is true for all values of the variables in the equality.
On the other hand, an equation is true only for certain values of its variables.
An equation is not an identity.
The following are the standard identities:
(a + b)²= a²+ 2ab + b²
(a – b)²= a²– 2ab +b²
(a + b)(a – b) = a²– b²
(x + a) (x + b) = x² + (a + b) x + ab
The above four identities are useful in carrying out squares and products of algebraic expressions.
They also allow easy alternative methods to calculate products of numbers and so on.
Coefficients: In the term of an expression any of the factors with the sign of the term is called the coefficient of the product of the other factors.
Terms: Various parts of an algebraic expression which are separated by + and – signs. Example: The expression 4x + 5 has two terms 4x and 5.
Constant Term: A term of expression having no lateral factor.
Like term: The term having the same literal factors. Example 2xy and -4xy are like terms.
(iii) Unlike term: The terms having different literal factors.
Example:
are unlike terms.
and 3xy
Factors: Each term in an algebraic expression is a product of one or more number (s) and/or literals. These number (s) and/or literal (s) are known as the factor of that term. A constant factor is called numerical factor, while a variable factor is known as
a literal factor. The term 4x is the product of its factors 4 and x.

Hindi Version
Dig Deep
Topic Level Resources
Sub – Topics
Select A Topic
Topic:
Chapters Index
Select Another Chapter
Assessments
Personalised Assessments
Assess
November 5, 2023
Rational Numbers | Study
Assess
Interact
Pre-Requisires
Test & Enrich
Pre – Requisite

English Version
Rational Numbers | Speed Notes
Notes For Quick Recap
Rational numbers are closed under the operations of addition, subtraction and multiplication, But not in division. (Scroll down to continue …)
Study Tools
Audio, Visual & Digital Content
The operations addition and multiplication are
(i) commutative for rational numbers.
(ii) associative for rational numbers.
The rational number 0 is the additive identity for rational numbers.
The additive inverse of the rational number a/b is -a/b and vice- versa.
The reciprocal or multiplicative inverse of the rational number
is if a/b is c/d if (a/b)(c/d) =1
Distributive property of rational numbers:
For all rational numbers a, b and c, a(b + c) = ab + ac
and a(b – c) = ab – ac.
Rational numbers can be represented on a number line.
Between any two given rational numbers there are countless rational numbers.
The idea of mean helps us to find rational numbers between two rational numbers.
Positive Rationals: Numerator and Denominator both are either positive or negative.
Example: 2/3, -4/-5
Positive Rationals: Numerator and Denominator both are either positive or negative.
Example: -2/3, 4/-5
.

Hindi Version
Dig Deep
Topic Level Resources
Sub – Topics
Select A Topic
Topic:
Chapters Index
Select Another Chapter
Assessments
Personalised Assessments
Assess
November 5, 2023
Linear Equations In One Variable | Study
Assess
Interact
Pre-Requisires
Test & Enrich
Pre – Requisite

English Version
Speed Notes
Notes For Quick Recap
A statement of equality of two algebraic expressions involving one or more variables. Example: x + 2 = 3
Linear Equation in One variable: The expressions which form the equation that contain single variable and the highest power of the variable in the equation is one. (Scroll down to continue …)
Study Tools
Audio, Visual & Digital Content
Linear Equations in One Variable
An algebraic equation is an equality involving variables. It says that the value of the expression on one side of the equality sign is equal to the value of the expression on the other side.
The equations we study in Classes VI, VII and VIII are linear equations in one variable. In such equations, the expressions which form the equation contain only one variable. Further, the equations are linear, i.e., the highest power of the variable appearing in the equation is 1.
A linear equation may have for its solution any rational number.
An equation may have linear expressions on both sides. Equations that we studied in Classes VI and VII had just a number on one side of the equation.
Just as numbers, variables can, also, be transposed from one side of the equation to the other.
Occasionally, the expressions forming equations have to be simplified before we can solve them by usual methods. Some equations may not even be linear to begin with, but they can be brought to a linear form by multiplying both sides of the equation by a suitable expression.
The utility of linear equations is in their diverse applications; different problems on numbers, ages, perimeters, combination of currency notes, and so on can be solved
using linear equations.

Hindi Version
Dig Deep
Topic Level Resources
Sub – Topics
Select A Topic
Topic:
Chapters Index
Select Another Chapter
Assessments
Personalised Assessments
Assess
November 5, 2023
CBSE 9 | Mathematics – Study – Premium
Educational Tools | Full Course
Study Tools
Audio, Visual & Digital Content
Assessment Tools
Assign, Assess & Analyse
November 5, 2023
CBSE 7 | Mathematics – Study – Free
Educational Tools | Full Course
Study Tools
Audio, Visual & Digital Content
Assessment Tools
Assign, Assess & Analyse
Connnect With Us
Enrich our growing community
[ultimatemember form_id=”26482″]
October 8, 2023
CBSE 7 | Mathematics – Study – Free
Educational Tools | Full Course
Study Tools
Audio, Visual & Digital Content
Assessment Tools
Assign, Assess & Analyse
Connnect With Us
Enrich our growing community
[ultimatemember form_id=”26482″]
September 5, 2023
CBSE 10 | Science – Study – Free
Educational Tools | Full Course
Study Tools
Audio, Visual & Digital Content
Assessment Tools
Assign, Assess & Analyse
September 5, 2023
CBSE 6 | Mathematics – Study – Premium
Educational Tools | Full Course
Study Tools
Audio, Visual & Digital Content
Assessment Tools
Assign, Assess & Analyse
August 22, 2023

S No.	Quadrilateral	Property	Image
1.	Kite	a. No Parallel Sides b. Two pairs of adjacent sides are equal.
2.	Trapezium	One pair of opposite sides is parallel.
3.	Parallelogram	Both pairs of opposite sides are parallel.
3.	Rectangle	a. Both the pair of opposite sides are parallel. b. Opposite sides are equal.c. All the four angles are 90°.
4.	Square	a. All four sides are equal. b. Opposite sides are parallel. c. All the four angles are 90°.
5.	Rhombus	a. All four sides are equal. b. Opposite sides are parallel. c. Opposite angles are equal.d. Diagonals intersect each other at the centre and at 90°.

Tag: Mathematics

Data Handling | Study

Simple Equations | Study

Lines and Angles | Study

Understanding Quadrilaterals | Study

CBSE 8 | Mathematics – Study – Premium

Direct And Inverse Proportions | Study

Factorisation | Study

Introduction to Graphs | Study

Exponents And Powers | Study

Data Handling | Study

Squares And Square Roots | Study

Cubes And Cube Roots | Study

Comparing Quantities | Study

Algebraic Expressions And Identities | Study

Rational Numbers | Study

Linear Equations In One Variable | Study

CBSE 9 | Mathematics – Study – Premium

CBSE 7 | Mathematics – Study – Free

CBSE 7 | Mathematics – Study – Free

CBSE 10 | Science – Study – Free

CBSE 6 | Mathematics – Study – Premium

Pre-Requisires

Data Handling | Speed Notes

Study Tools

Dig Deep

Sub – Topics

Chapters Index

Assessments

Pre-Requisires

Simple Equations | Speed Notes

Study Tools

Dig Deep

Sub – Topics

Chapters Index

Assessments

Pre-Requisires

Speed Notes

Study Tools

Dig Deep

Sub – Topics

Chapters Index

Assessments

Pre-Requisires

Speed Notes

Study Tools

Quadrilateral

Characteristics of a quadrilateral

Angle Sum Property of a Quadrilateral:

Types Of Quadrilaterals

Kite:

Characteristics Of Kite:

Perimeter Of Square

Area Of Kite

Trapezium:

Characteristics Of Trapezium

Types Of Trapezium:

Isosceles Trapezium:

Characteristics Of Isosceles Trapezium

Scalene Trapezium:

Characteristics Of Scalene Trapezium

Right Trapezium:

Characteristics Of Right Trapezium

Perimeter Of Trapezium

Area Of Trapezium

Parallelogram:

Characteristics of a parallelogram

Types Of Parallelogram

Perimeter Of Parallelogram

Area Of Parallelogram

Rectangle:

Characteristics Of Rectangle

Perimeter Of Rectangle

Area Of Recatangle

Rhombus:

Characteristics Of Rhombus

Perimeter Of Rhombus

Area Of Rhombus

Square:

Characteristics Of Square