Pre-Requisires
Test & Enrich
Basic Geometrical Ideas | Speed Notes
Notes For Quick Recap
Geometry
Geometry is a branch of mathematics concerned with properties of space such as the distance, shape, size, and relative position of figures. A mathematician who works in the field of geometry is called a 🎉geometer. (Scroll down to continue …)
Study Tools
Audio, Visual & Digital Content
Basic Geometrical Ideas | Speed Notes
Notes For Quick Recap
Geometry
Geometry is a branch of mathematics concerned with properties of space such as the distance, shape, size, and relative position of figures. A mathematician who works in the field of geometry is called a 🎉geometer.
Space
Space: space refers to a set of points that form a particular type of structure.
Plane
A plane is a flat surface that extends infinitely in all directions
Point
Point is an exact position or location in space with no dimensions.
Mathematically, a point is defined as a circle with zero radius.
Since it is not possible its is represented by a very small dot.
A point is usually represented by a capital letter.
In mathematical terms, pont is a cirlce with no radius. It does mean that a very very small circle.
A point determines a location. It is usually denoted by a capital letter.
Lines And Its Types
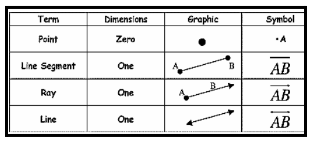
Ray
A Ray is a straight path that stars at a point and extends infinitely in one direction.
Note: A ray is a portion of line starting at a point and extends in one direction endlessly. A ray has only one endpoint (Initial point).
Line or Straight Line
A line is a straight path that extends infinitely in two opposite directions. It can be treated as a combination of two rays starting from the same point but extending in the opposite directions.
Note: A line has no end points.
Line Segment:
A line segment is the part of a line between two points. (Segment means part).
The length of a line segment is the shortest length between two end points.
The line segment has two end points. Note: A line Segment has two endpoints. (both Initial and end points). (Scroll down to continue …).
Intersecting Lines and Non-intersecting Lines
Intersecting And Parallel Lines
Parallel Lines
The lines which never cross each other at any point are called Parallel lines or Non-intersecting lines.
In other words, lines that are always the same distance apart from each other and that never meet are called Parallel lines Or Non-intersecting lines.
The perpendicular length between two lines is the distance between parallel lines.
Note: Parallel lines do not have any common point.
Intersecting Lines
The lines which cross (meet) each other at a point are called Intersecting Lines or non-parallel lines.
Intersecting lines meet at only one point.
Angle
An angle is made up of two rays starting from a common end point.

An angle leads to three divisions of a region:
On the angle, the interior of the angle and the exterior of the angle.
Curve
Curve is a drawing (straight or non-straight) made without lifting the pencil may be called a curve.
Note: In this sense, a line is also a curve.
Types of Curves
Cureves are two types. They are (i) Simple or Open curve (ii) Closed curve.
Simple Curve
Simple or open curve is a curve that does not cross (intersect) itself.
Closed Curve
Closed curve is a curve that crosses (intersects) itself.
Curves–Concave And Convex
In geometry, a curve is a line or shape that is drawn smoothly and continuously in a plane with bends or turns.
Mathematicians define a curve as any shape that can be drawn without lifting the pen.
In Mathematics, A curve is a continuous and smooth line that is defined by a mathematical function or parametric equations.
Concave And Convex curves:
Curves are of two types. They are concave curve and convex curve.
Concave Curve:
A curve is concave is a curve that curves inward, resembling a cave.
Examples:
– The interior of a circle.
– The graph of a concave function like y = -x2.
Convex Curves:
A curve is convex if it curves outward.
Examples:
– The exterior of a circle.
– The graph of a convex function like y = x2.
Polygon
A polygon is a simple closed figure formed by the line segments.
Part of Polygon
(i) Sides Of The Polygon
The line segments of a polygone are called sides of the polygon.
(ii) Adjacent Sides Of Polygon
Adjacent sides of a polygon are thesides of a polygon with a common end point.
(iii) Vertex Of Polygon
Vertext of a polygon is a point at which a pair of sides meet.
(iv) Adjacent Vertices
Adjacent vertices of polygon are the end points of the same side of the polygon.
(v) diagonal
Diagonal of a polygone is a line segment that joins the non-adjacent vertices of the polygon.
Triangle
A triangle is a three-sided polygon.
In other terms triangle is a three sided closed figure.
Quadrilateral
A quadrilateral is a four-sided polygon. (It shouldbe named cyclically).
In any

similar relations exist for the other three angles.
Circle And Its Parts
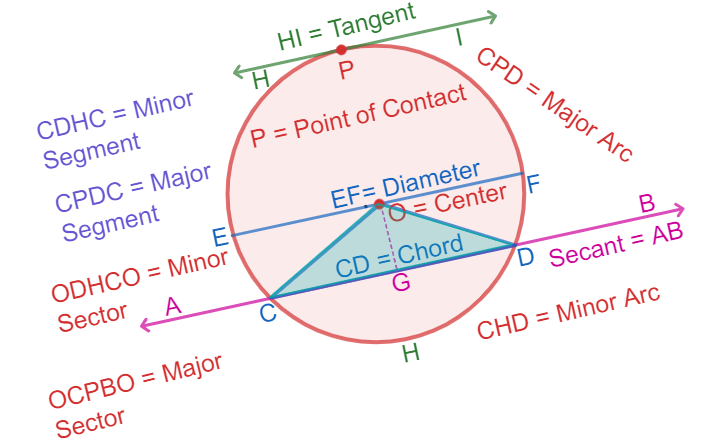
A circle is the path of a point moving at the same distance from a fixed point.
Centre Of Circle
Centre Of Circle is a point that is equidistant from any point on the boundary of the circle.
In other words the centre of the circles is a centre point of the circle.
Radius Of Circle
Radius of circle is the distance between the centre of the circle and any point on the boundary of the circle.
Circumference Of Circle
Circumference of circle is the length of the boundary of the circle.
Chord Of Circle
A chord of a circle is a line segment joining any two points on the circle.
A diameter is a chord passing throughthe Centre of the circle.
Sector Of Circle
A sector is the region in the interior of a circle enclosed by an arc on one side and a pair of radii on the other two sides.
Segment Of Circle
A segment of a circle is a region in the interior of the circle enclosed by an arc and a chord.
The diameter of a circle divides it into two semi-circles.
The diameter of a circle divides it into two semi-circles.
Dig Deep
Topic Level Resources
Sub – Topics
Select A Topic
Topic:
Chapters Index
Select Another Chapter
Assessments
Personalised Assessments



Leave a Reply
You must be logged in to post a comment.