4. A fraction whose numerator is less than the denominator is called a proper fraction.

5. A fraction whose numerator is more than or equal to the denominator is called animproper fraction.

6. A combination of a whole number and a proper fraction is called a mixed fraction.

7. To get a fractionequivalent to a given fraction,we multiply (or divide) its numerator and denominator by the same non-zero number.

8. Fractions having the same denominators are called like fractions. Otherwise, they are calledunlike fractions.

9. A fraction is said to be in its lowest termsif its numerator and denominator have no commonfactor other than 1.

10. To compare fractions, we use the followingsteps:

Step I Find the LCMof the denominators of the given fractions.

Step II Converteach fraction to itsequivalent fraction with denominator equal to the LCM obtained in step I.

Step Ill Arrangethe fractions in ascending or descending order byarranging numerators in ascending or descending order.

11. To convert unlike fractions into like fractions, we use the following steps:Step I Find the LCM of the denominators of the given fractions.

Step II Convert each of the given fractions into an equivalent fraction having denominator equal to the LCM obtained in step I.

12. To add (or subtract)fractions, we may use the following steps:Step I Obtain the fractionsand their denominators.

Step II Find the LCMof the denominators.

Step III Convert each fraction into an equivalent fraction having its denominator equal to the LCM obtainedin step II.

Step IV Add (or subtract) like fractions obtained in Step Ill.

Step III Convert each fraction into an equivalent fraction having its denominator equal to the LCM obtainedin step II.

Step IV Add (or subtract) like fractions obtained in Step Ill.

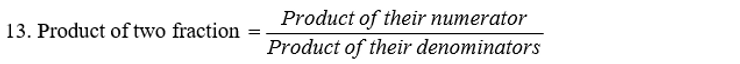
14. Two fractions are said to be reciprocal of each other, if their product is 1. The reciprocal of a non zero fraction a/b is b/a.

15. The divisionof a fraction a/b by a non-zero fraction c/d is the product of a/b with the

reciprocal of c/d.

Decimals:

1. Decimals are an extension of our number system.

2. Decimals are fractionswhose denominators are 10, 100, 1000 etc.

3. A decimal has two parts, namely, the whole numberpart and decimal part.

4. The number of digits containedin the decimal part of a decimal number is known as the numberof decimal places.

5. Decimals having the same number of places are called like decimals, otherwise they are knownas unlike decimals.

6. We have, 0.1 = 0.10 = 0.100 etc, 0.5 = 0.50 = 0.500 etc and so on. That is by annexing zeros on the right side of the extreme right digit of the decimalpart of a number does not alterthe value of the number.

7. Unlike decimals may be converted into like decimals by annexing the requisite numberof zeros on the right side of the extreme right digit in the decimal part.

8. Decimal numbers may be convertedby using the following steps.Step I Obtain the decimalnumbers

Step II Compare the whole partsof the numbers. The number with greater whole part will be greater. If the whole parts are equal, go to next step.

Step Ill Compare the extreme left digits of the decimal parts of two numbers. The number with greater extreme left digit will be greater. If the extreme left digits of decimal parts are equal,then compare the next digits and so on.

9. A decimal can be converted into a fractionby using the following steps:Step I: Obtain the decimal.

Step II: Take the numerator as the number obtained by removing the decimal point from the given decimal.

Step III: Take the denominator as the number obtainedby inserting as many zeros with 1 (e.g.10, 100 or 1000 etc.)as there are number of places in the decimal part.

10. Fractions can be converted into decimals by using the following steps:

Step I: Obtain the fractionand convert it into an equivalent fraction with denominator 10 or 100 or 1000 if it is not so.

Step II: Write its numeratorand mark decimal point after one place or two places or threeplaces from right towards left if the denominator is 10 or 100 or 1000 respectively. If the numerator is short of digits, insert zeros at the left of the numerator.

11. Decimals can be added or subtracted by using the following steps:Step I: Convert the given decimals to like decimals.

Step II: Write the decimals in columns with their decimal pointsdirectly below each other so that tenthscome under tenths, hundredths come and hundredths and so on.

Step III: Addor subtract as we add or subtract whole numbers.

Step IV: Place the decimal point, in the answer, directly below the other decimal points.

12. In order to multiply a decimal by 10, 100, 1000 etc., we use the following rules:

Rule I: On multiplying a decimal by 10, the decimalpoint is shiftedto the right by one place.

Rule II: On multiplying a decimal by 100, the decimal point is shiftedto the right by two places.

Rule III: On multiplying a decimal by 1000, the decimal point is shiftedto the right by threeplaces, and so on.

13. A decimal can be multiplied by a whole number by using following steps:

Step I: Multiply the decimal without the decimalpoint by the given whole number.

Step II: Mark the decimal point in the product to have as many placesof decimal as are there in the given decimal.

14. To multiply a decimal by another decimal, we follow following steps:

Step I: Multiply the two decimalswithout decimal point just like whole numbers.

Step II: Insert the decimal point in the product by countingas many places from the right to left as the sum of the number of decimalplaces of the given decimals.

15. A decimal can be dividedby 10, 100, 1000 etc by using the followingrules:

Rule I When a decimal is divided by 10, the decimal point is shifted to the left by one place.

Rule II When a decimal is divided by 100, the decimal point is shifted to the left by two places.

Rule III When a decimal is divided by 1000, the decimal point is shiftedto the left by threeplaces.

16. A decimal can be divided by a whole number by using the following steps:Step I: Check the whole number part of the dividend.

Step II: If the wholenumber part of the dividend is less than the divisor,then place a 0 in the onesplace in the quotient. Otherwise, go to step Ill.

Step III: Divide the whole number part of the dividend.

Step IV: Place the decimal point to the right of ones place in the quotient obtained in step I.

Step V: Divide the decimal part of the dividend by the divisor. If the digits of the dividend are exhausted, then place zeros to the right of dividendand remainder each time and continue the process.

17. A decimal can be divided by a decimal by using the following steps:

Step 1 Multiple the dividend and divisor by 10 or 100 or 1000 etc. to convert the divisor into a whole number.

Step II Divide the new dividendby the whole number obtainedin step I.

Extra: