Pre-Requisires
Test & Enrich
Lines And Angles | Speed Notes
Notes For Quick Recap
Basic Terms And Definitions
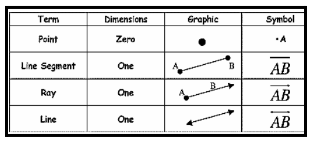
1. Point – A Point is that which has no component. It is represented by a dot.
A point is shown with a capital letter.
Examples: A, B, C …..
Linear And Colinear Points
5. Collinear points: Points lying on the same line are called Collinear Points.
Non-collinear points: Points which do not lie on the same line are called Non-Collinear Points.
Line – When we join two distinct points then we get a line. A line has no endpoints; it can be extended on both sides infinitely.
Line Segment Line – Segment is the part of the line which has two endpoints.
Ray – Ray is also a part of the line that has only one endpoint and has no end on the other side. (Scroll to continue …)
Study Tools
Audio, Visual & Digital Content
Lines And Their Types
Ray
A Ray is a straight path that stars at a point and extends infinitely in one direction.
Note: A ray is a portion of line starting at a point and extends in one direction endlessly. A ray has only one endpoint (Initial point).
Line or Straight Line
A line is a straight path that extends infinitely in two opposite directions. It can be treated as a combination of two rays starting from the same point but extending in the opposite directions.
Note: A line has no end points.
Line Segment:
A line segment is the part of a line between two points. (Segment means part).
The length of a line segment is the shortest length between two endpoints.
The line segment has two endpoints. Note: A line Segment has two endpoints. (both Initial and end points).
Intersecting Lines and Non-intersecting Lines
Intersecting Lines
Lines that meet or cross at a point with each other are called intersecting lines Or Non-parallel lines.
Intersecting lines meet at a point.
Parallel Lines
Lines that are always the same distance apart from each other and that never meet are called Parallel lines or Non-intersecting lines.
Note: Parallel lines do not have any common point.
Angles
When two rays begin from the same endpoint then they form an Angle. The two rays are the arms of the angle and the endpoint is the vertex of the angle.
Types of Angles By Measure
| Angle | Notation | Image |
| Acute | An angle which is between 0° and 90°. | |
| Right | An angle which is exactly equal to 90°. | |
| Obtuse | An angle which is between 90° and 180°. | |
| Reflex | An angle which is between 180° and 360° | |
| Straight | An angle which is exactly equal to 180°. | |
| Complete | An angle which is exactly equal to 360°. |
Complementary and Supplementary Angles
Complementary Angles are the different angles whose sum is 90°.
Suplementary Angles are the different angles whose sum is 180°

Angles Based On Position
Adjacent Angles: Two angles that share a common side and a common vertex, but do not overlap.
Linear Pair: A pair of adjacent angles whose non-common sides form a straight line (i.e., they are supplementary and add up to 180°).
Vertical (Opposite) Angles:
Angles opposite each other when two lines intersect. They are always equal.
Angles:
An angle is formed by two rays(called the sides or arms of the angle) with a common endpoint called the vertex.
Angles are measured in degrees(°) or radians, with a full rotation being 360°.
Special Angle Pairs:
Complementary Angles:
Two angles whose measures add up to 90°.
Supplementary Angles: Two angles whose measures add up to 180°
Angles in Polygons:
Interior Angles: Angles on the inside of a polygon. The sum of the interior angles of an n-sided polygon is \((n-2) \times 180°\).
Exterior Angles: Angles on the outside of a polygon. The sum of the exterior angles of any polygon is always 360°.
Angles Formed by Parallel Lines and Transversals:
When a transversal intersects two parallel lines, several angle pairs are formed:
Corresponding Angles: Angles in the same position relative to the two lines and the transversal. They are equal.
Alternate Interior Angles: Angles on opposite sides of the transversal and inside the parallel lines. They are equal.
Alternate Exterior Angles: Angles on opposite sides of the transversal and outside the parallel lines. They are equal.
– **Consecutive (Same-Side) Interior Angles:** Angles on the same side of the transversal and inside the parallel lines. They are supplementary.
Measuring Angles:
Protractor: A tool used to measure angles in degrees.
Radians: Another unit of angle measure. One full revolution (360°) is equal to \(2\pi\) radians.
Angle Relationships in Circles:
Central Angle: An angle whose vertex is the centre of the circle. The measure of a central angle is equal to the measure of the arc it intercepts.
Inscribed Angle: An angle whose vertex is on the circle and whose sides contain chords of the circle. The measure of an inscribed angle is half the measure of the intercepted arc.
Angles Formed by Tangents and Chords: The measure of the angle formed by a tangent and a chord through the point of contact is half the measure of the intercepted arc.
Angles Inside the Circle (but not at the centre): The measure of an angle formed by two intersecting chords is half the sum of the measures of the arcs intercepted by the angle and its vertical angle.
Trigonometric Angles:
Standard Position: An angle with its vertex at the origin and one side on the positive x-axis.
Reference Angle: The acute angle formed by the terminal side of an angle and the x-axis.
Quadrantal Angles: Angles that are multiples of 90° (0°, 90°, 180°, 270°, 360°).
Angle Conversions:
Degrees to Radians: Multiply the number of degrees by \(\frac{\pi}{180}\).
Radians to Degrees: Multiply the number of radians by \(\frac{180}{\pi}\).
Key Properties and Theorems:
Angle Sum Property of a Triangle:
The sum of the interior angles of a triangle is always 180°.
Exterior Angle Theorem:
The measure of an exterior angle of a triangle is equal to the sum of the measures of the two non-adjacent interior angles.
Polygon Interior Angles Theorem:
The sum of the interior angles of an n-sided polygon is \((n-2) \times 180°\).
Understanding these fundamental aspects of angles will enhance your comprehension of geometric principles and their applications.
Pairs of Angles Axioms
1. If a ray stands on a line, then the sum of two adjacent angles formed by that ray is 180°.
This shows that the common arm of the two angles is the ray which is standing on a line and the two adjacent angles are the linear pair of the angles. As the sum of two angles is 180° so these are supplementary angles too.
2. If the sum of two adjacent angles is 180°, then the arms which are not common of the angles form a line.
This is the reverse of the first axiom which says that the opposite is also true.
Vertically opposite Angles Theorem
When two lines intersect each other, then the vertically opposite angles so formed will be equal.
AC and BD are intersecting each other so ∠AOD = ∠BOC and ∠AOB = DOC.
Parallel Lines and a Transversal
If a line passes through two distinct lines and intersects them at distant points then this line is called Transversal Line.
Here line “l” is transversal of line m and n.
Exterior Angles – ∠1, ∠2, ∠7 and ∠8
Interior Angles – ∠3, ∠4, ∠5 and ∠6
Pairs of angles formed when a transversal intersects two lines-
1. Corresponding Angles:
- ∠ 1 and ∠ 5
- ∠ 2 and ∠ 6
- ∠ 4 and ∠ 8
- ∠ 3 and ∠ 7
2. Alternate Interior Angles:
- ∠ 4 and ∠ 6
- ∠ 3 and ∠ 5
3. Alternate Exterior Angles:
- ∠ 1 and ∠ 7
- ∠ 2 and ∠ 8
4. Interior Angles on the same side of the transversal:
- ∠ 4 and ∠ 5
- ∠ 3 and ∠ 6
Transversal Axioms
1. If a transversal intersects two parallel lines, then
- Each pair of corresponding angles will be equal.
- Each pair of alternate interior angles will be equal.
- Each pair of interior angles on the same side of the transversal will be supplementary.
2. If a transversal intersects two lines in such a way that
- Corresponding angles are equal then these two lines will be parallel to each other.
- Alternate interior angles are equal then the two lines will be parallel.
- Interior angles on the same side of the transversal are supplementary then the two lines will be parallel.
Lines Parallel To The Same Line
If two lines are parallel with a common line then these two lines will also be parallel to each other.
As in the above figure if AB ∥ CD and EF ∥ CD then AB ∥ EF.
Angle Sum Property of a Triangle
1. The sum of the angles of a triangle is 180º.
∠A + ∠B + ∠C = 180°
2. If we produce any side of a triangle, then the exterior angle formed is equal to the sum of the two interior opposite angles.
∠BCD = ∠BAC + ∠ABC.
Dig Deep
Topic Level Resources
Sub – Topics
Select A Topic
Topic:
Chapters Index
Select Another Chapter
Assessments
Personalised Assessments



Leave a Reply
You must be logged in to post a comment.