Pre-Requisires
Test & Enrich
Triangles | Speed Notes
Notes For Quick Recap
Similar Geometric Figures:
Two geometric figures which are the same in shape, such that one is simply a copy of the other on a smaller scale or a larger scale, are called similar geometric figures.
Two geometric figures are said to be similar if and only if they have the same shape but not necessarily the same size. Two congruent geometric figures are always similar but converse may or may not be true. (Scroll down to read more …)
Study Tools
Audio, Visual & Digital Content
Similar Polygons: Two polygons of the same number of sides are similar, if
(i) their corresponding angles are equal and
(ii) their corresponding sides are in proportion or their corresponding sides are in the same ratio.
The same ratio of the corresponding sides is referred to as the representative fraction or the scale factor for the polygons.
Similar Triangles :
Two triangles are said to be similar,
if (i) their corresponding angles are equal and
ii) their corresponding sides are in proportion (are in the same ratio).
Basic Proportionality Theorem (or Thales Theorem) : 1
If a line is drawn parallel to one side of a triangle intersecting the other two sides, then it divides the two sides in the same ratio. Or If a line is drawn parallel to one side of a triangle, intersecting the other two sides in distinct points, the other two sides are divided in the same ratio i .e.. If in ∆ABC, l∥ BC, intersecting in D and E. then

Converse of Basic Proportionality Theorem :

If a line divides any two sides of a triangle in the sameratio, the line is parallel to the third side i.e.
In ∆ABC, if l intersects AB in D and AC in E, such that:
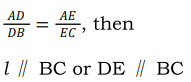
Criteria for Similarity of Triangles:
Two triangles are said to be similar, if
(i) their corresponding angles are equal and (ii) their corresponding sides are in proportion (or are in the same ratio).
2 (i) AA or AAA Similarity Criterion : If two angles of one triangle are equal to two corresponding angles of another triangle, then the triangles are similar. If two angles of one triangle are respectively equal to the two angles of another triangle, then the third angles of the two triangles are necessarily equal, because the sum of three angles of a triangle is always 180 0 .
(ii) SAS Similarity Criterion : If one angle of a triangle is equal to one angle of another triangle and the sides including these angles are in the same ratio, then the two triangles are similar. Or If two sides of a triangle are proportional to two corresponding sides of another triangle and the angles included between them are equal, then the triangles are similar.
iii) SSS Similarity Criterion : If in two triangles, sides of one triangle are proportional (or are in the same ratio) to the sides of the other triangle, then the triangles are similar. If ∆ABC~ ∆PQR by any one similarity criterion, then ∠A=∠P, ∠B=∠Q, ∠C=∠R and
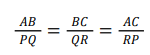
i.e., A and P, B and Q, C and R are the corresponding vertices, also AB and PQ. BC and QR. CA and RP are the corresponding sides. 3 Areas of Similar Triangles: The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides. – The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding medians. – The ratio of the areas of two similar triangles is equal to the ratio of the squares of their corresponding altitudes. – The ratio of the areas of two similar triangles is equal to the ratio of the squares of their corresponding angle bisectors. Pythagoras Theorem : In a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides. Converse of Pythagoras Theorem : In a triangle, if the square of one side is equal to the sum of the squares of the other two sides, then the angle opposite the first side is a right angle. If a perpendicular is drawn from the vertex of the right angle of a right triangle to the hypotenuse, the triangles on each side of the perpendicular are similar to the whole triangle and similar to each other i .e ..
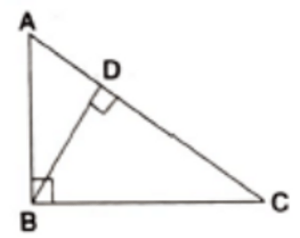
If in ∆ABC, ∠B=90^0 and BD ⊥ AC, then (i) ∆ADB ~ ∆ABC (ii) ∆BDC ~ ∆ABC (iii) ∆ADB ~ ∆BDC
Dig Deep
Topic Level Resources
Sub – Topics
Select A Topic
Topic:
Chapters Index
Select Another Chapter
Assessments
Personalised Assessments



Leave a Reply
You must be logged in to post a comment.